动态规划详解Python-编程知识

动态规划

动态规划（Dynamic Programming）是一种用于解决复杂问题的算法设计方法。它通常用于优化问题，其中问题可以被分解成一系列重叠子问题，通过存储并重复使用已经解决过的子问题的解，可以避免重复计算，从而提高算法的效率。

动态规划的基本思想是将原始问题分解成若干个子问题，并逐个求解这些子问题的最优解。通过定义状态和状态转移方程，可以将问题的求解转化为一个递推过程，从而得到最优解。

动态规划算法的核心步骤通常包括以下几个方面：

定义问题的状态：将原始问题抽象为一个或多个子问题，并定义状态来表示子问题的解。
确定状态转移方程：通过分析子问题之间的关系，建立状态之间的转移方程，描述当前状态和之前状态之间的关系。
确定初始条件：确定最简单的子问题的解，即初始状态的值。
递推求解：使用状态转移方程和初始条件，逐步计算出更复杂的子问题的解，直到得到原始问题的解。
解析解：根据子问题的解，逐步还原出原始问题的解。

动态规划算法通常具有较高的时间复杂度，但通过存储已解决的子问题的解，可以大大减少重复计算，提高算法效率。它在许多领域有广泛的应用，如组合优化、图论、序列比对、路径规划等。

斐波那契数列

这里简单的解释一下斐波那契数列：F(0) = 0 , F(1) = 1
F(N) = F(N-1) + F(N-2) , N>1 数列前几项如下：
0 1 1 2 3 5 8 13 21…

递归代码和非递归代码比较

import timedef calculate_time(func):def wrapper(*args, **kwargs):start_time = time.time()result = func(*args, **kwargs)end_time = time.time()execution_time = end_time - start_timeprint(f"函数 {func.__name__} 的执行时间为：{execution_time} 秒")return resultreturn wrapper@calculate_time
def func1(n):return _func1(n)# 存在大量的子问题重复计算
def _func1(n):if n <= 1:return nreturn _func1(n - 1) + _func1(n - 2)# 把需要用到的子问题存起来
@calculate_time
def func2(n):f = [0, 1]if n > 1:for i in range(n - 1):num = f[-1] + f[-2]f.append(num)return f[n]print(func1(36))
print(func2(36))

运行结果：
函数 func1 的执行时间为：3.150125503540039 秒
14930352
函数 func2 的执行时间为：0.0 秒
14930352

爬楼梯

问题：有一个楼梯，总共有10级台阶，每次只能走一级或者两级台阶，全部走完，有多少种走法？

找规律得到递推式：
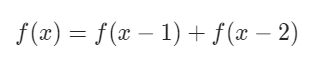
在这里插入图片描述

def climbStairs(self, n: int) -> int:f = [0,1,2]if n > 2:for i in range(n-2):r = f[-1] + f[-2]f.append(r)return f[n]

最大回撤

问题：有一个数组，求其中两个数x,y，满足x的索引小于y的索引，使得 x-y 最大。例如 arr = [3,7,2,6,4,1,9,8,5]，最大回撤是6，对应的x=7,y=1。

初始时，设max_drop=0，peak都设为arr[0]。然后从左到右遍历数组，对于每个元素price：

如果price大于peak，更新peak为当前的price。
否则，计算当前的回撤值drop，即peak - price。
如果drop大于max_drop，更新max_drop为当前的drop。

最终，max_drop就是最大回撤的值。

# 只返回最大回撤的金额
def calculate_max_drawdown(arr):max_drop = 0peak = arr[0]for i in range(1, len(arr)):if arr[i] > peak:peak = arr[i]else:drop = peak - arr[i]if drop > max_drop:max_drop = dropreturn max_drop# 示例用法
arr = [3, 7, 2, 6, 4, 1, 9, 8, 5]
max_drawdown = calculate_max_drawdown(arr)
print(max_drawdown)  # 输出: 6

要求计算出最大回撤，并且对应的返回x和y
可以使用动态规划的思想来解决这个问题。我们可以定义一个变量max_sum来跟踪当前的最大子数组和，以及一个变量current_sum来记录当前的子数组和。

初始时，将max_sum和current_sum都设为数组中的第一个元素。然后从数组的第二个元素开始遍历，对于每个元素num：

将current_sum与0比较，取其中较大的值，并将num加到current_sum中，得到新的current_sum。
将current_sum与max_sum比较，取其中较大的值，并将结果赋给max_sum。

最终，max_sum就是最大连续子数组的和。

def calculate_max_drawdown(arr):max_drop = 0peak = 0start_index = 0end_index = 0for i, price in enumerate(arr):if price > peak:peak = priceelse:drop = peak - priceif drop > max_drop:max_drop = dropstart_index = arr.index(peak)end_index = ireturn max_drop, start_index, end_index# 示例用法
arr = [3, 7, 2, 6, 4, 1, 9, 8, 5]
max_drawdown, start_index, end_index = calculate_max_drawdown(arr)
print("最大回撤：", max_drawdown)
print("起始索引：", start_index)
print("结束索引：", end_index)

输出：
最大回撤： 6
起始索引： 1
结束索引： 4

最大连续子数组和

问题：给定一个数组，求其最大连续子数组的和。例如：arr = [1,5,-10,2,5,-3,2,6,-3,1]. 输出为：12。对应的连续子数组为 [2,5,-3,2,6]。

def max_subarray_sum(arr):max_sum = arr[0]current_sum = arr[0]for num in arr[1:]:current_sum = max(num, current_sum + num)max_sum = max(max_sum, current_sum)return max_sum# 示例用法
arr = [1, 5, -10, 2, 5, -3, 2, 6, -3, 1]
max_sum = max_subarray_sum(arr)
print(max_sum)  # 输出: 12

"""同时输出对应的子数组"""
def max_subarray_sum(arr):max_sum = arr[0]current_sum = arr[0]start_index = 0end_index = 0temp_start_index = 0for i, num in enumerate(arr[1:], start=1):if num > current_sum + num:temp_start_index = icurrent_sum = numelse:current_sum = current_sum + numif current_sum > max_sum:start_index = temp_start_indexend_index = imax_sum = current_sumsubarray = arr[start_index:end_index + 1]return max_sum, subarray# 示例用法
arr = [1, 5, -10, 2, 5, -3, 2, 6, -3, 1]
max_sum, subarray = max_subarray_sum(arr)
print("最大连续子数组和：", max_sum)
print("最大连续子数组：", subarray)

输出：
最大连续子数组和： 12
最大连续子数组： [2, 5, -3, 2, 6]

最长不重复子串

题目形式：给定一个字符串，找出没有重复字符的最长的子串。例如输入“abcbefgf”，答案是 “cbefg”。

算法步骤如下：

定义两个指针，start 和 end，分别表示滑动窗口的起始位置和
结束位置，初始时两个指针都指向字符串的开头。
定义一个集合 seen，用于存储滑动窗口中出现过的字符。
定义两个变量 max_length 和 max_substring，分别用于记录最长子串的长度和内容，初始时都为 0。开始遍历字符串，从左到右依次移动 end 指针：
—a.如果当前字符 s[end] 在集合 seen 中不存在，说明是一个新的字符，将其加入 seen 中，并更新 end 指针。
—b.如果当前字符 s[end] 在集合 seen 中已经存在，说明遇到了重复字符。此时需要移动 start 指针，并更新 seen 集合，直到滑动窗口中不再有重复字符。

—c.在每次移动 end 指针时，都需要更新 max_length 和 max_substring，以记录当前的最长子串。
遍历结束后，返回最长子串 max_substring。

def longest_unique_substring(s):start = 0end = 0seen = set()max_length = 0max_substring = ""while end < len(s):if s[end] not in seen:seen.add(s[end])end += 1else:if end - start > max_length:max_length = end - startmax_substring = s[start:end]seen.remove(s[start])start += 1if end - start > max_length:max_substring = s[start:end]return max_substring# 示例用法
s = "abcbefgf"
result = longest_unique_substring(s)
print(result)  # 输出: "cbefg"

全排列

问题：给定一个数组，找出其所有可能的排列。例如: arr = [1,1,3]，输出为 [[1,1,3],[1,3,1],[3,1,1]]。

def permute_unique(nums):# 定义递归函数，生成给定位置上的所有可能排列def backtrack(start):# 终止条件：当遍历到数组末尾时，将当前生成的排列加入结果集if start == len(nums):permutations.append(nums[:])  # 将当前排列加入结果集return# 使用一个集合来记录已经选择过的元素，避免重复生成相同的排列used = set()# 从当前位置开始，依次尝试每个元素作为当前位置的元素for i in range(start, len(nums)):# 如果当前元素已经被选择过，则跳过if nums[i] in used:continue# 进行选择：将当前元素加入路径，并标记为已选择used.add(nums[i])nums[start], nums[i] = nums[i], nums[start]# 递归调用自身，在新的位置上生成剩余元素的所有可能排列backtrack(start + 1)# 撤销选择：将当前选择的元素从路径中移除，并将其标记为未选择，以便进行下一次选择nums[start], nums[i] = nums[i], nums[start]used.remove(nums[i])permutations = []  # 结果集，用于存储所有排列backtrack(0)  # 从位置0开始生成所有排列return permutations# 示例用法
nums = [1, 1, 3]
result = permute_unique(nums)
print(result)

快速排序+二分查找

def partition(lst, left, right):temp = lst[left]while left < right:while left < right and lst[right] >= temp:right -= 1lst[left] = lst[right]while left < right and lst[left] <= temp:left += 1lst[right] = lst[left]lst[left] = tempreturn leftarr = [5, 2, 8, 6, 3]print(partition(arr, 0, len(arr) - 1))def quick_sort(lst, left, right):if left < right:mid = partition(lst, left, right)quick_sort(lst, left, mid)quick_sort(lst, mid + 1, right)quick_sort(arr, 0, len(arr) - 1)
print(arr)#  二分查找只适用于在有序序列中查找元素
def binary_search(lst, val):left = 0right = len(lst) - 1while left <= right:mid = (left + right) // 2if lst[mid] == val:return midelif lst[mid] > val:  # 说明要查找的值在mid的左边right = mid - 1else:  # 说明要查找的值在mid的右边、left = mid + 1# 代码执行至此说明没有找到元素val，返回-1return -1
# 注意：mid定义在while循环里面print(binary_search(arr, 8))

输出：
2
[2, 3, 5, 6, 8]
4

合并两个有序数组（归并排序）

题目形式：给定两个按升序排列的有序数组，将它们合并成一个新的有序数组。例如：a = [1,2,6,8], b = [2,4,7,10]，输出为 arr = [1,2,2,4,6,7,8,10]

# 定义合并函数，将两个有序序列合并为一个有序序列
def merge(lst, left, mid, right):"""思路：定义一个列表merged，循环比较两个有序序列的首元素大小，并放入临时空列表。"""if left < right:merged = []i = leftj = mid + 1while i <= mid and j <= right:if lst[i] < lst[j]:merged.append(lst[i])i += 1else:merged.append(lst[j])j += 1# 代码执行至此，有一个序列元素为空，另一个不为空，接下来将剩下的元素放入空列表while i <= mid:merged.append(lst[i])i += 1while j <= right:merged.append(lst[j])j += 1lst[left:right + 1] = mergedreturn lstdef _merge_sort(lst, left, right):if left < right:mid = (left + right) // 2_merge_sort(lst, left, mid)_merge_sort(lst, mid + 1, right)merge(lst, left, mid, right)@calculate_time
def merge_sort(lst):_merge_sort(lst, 0, len(lst) - 1)if __name__ == '__main__':# 测试代码lst = list(range(10000))random.shuffle(lst)print(lst)merge_sort(lst)print(lst)

三数之和

def sum_of_three(arr,target):assert len(arr)>=3,"len(arr) should >=3!"arr.sort()ans = set()for k,c in enumerate(arr):i,j = k+1,len(arr)-1while i<j:if arr[i]+arr[j]+c <target:i = i+1elif arr[i]+arr[j]+c > target:j = j-1else:ans.update({(arr[k],arr[i],arr[j])})i = i+1j = j-1return(list(ans))print(sum_of_three([-3,-1,-2,1,2,3],0))