---

前言

这一节内容介绍的是FM信号的抗噪声性能，与之前学的幅度调制不同，角度调制系统是非线性的，其信噪比的推导计算很多地方添加了假设，最后得到一个估计值。当初我学这部分内容的时候似乎推导并不要求掌握，只需要记住结论即可，可以按需学习。

---

一、FM的解调

FM信号的解调需要用到一个特殊的模块——鉴频器，它的作用是能够取出输入信号的瞬时频偏。首先我们知道输入信号$r(t)$的表达式为：

$r(t)=s(t)+n(t)$

其中，$n(t)$为带宽为$2\beta W+2W$的窄带高斯噪声，$W$为原信号带宽。我们假设带宽为$2\beta W+2W$的BPF能够让$s(t)$完整通过（实际上不可能，因为这个带宽只是卡松公式的估计带宽）。

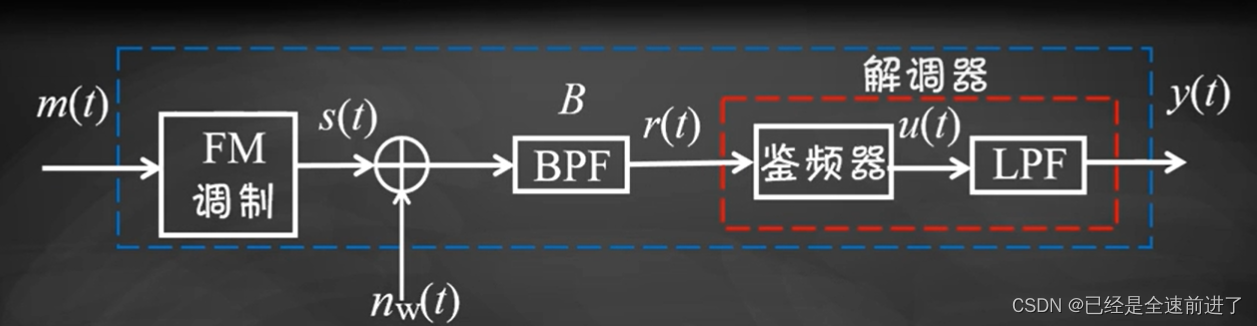
二、FM的输出信噪比

鉴频器首先能输出调制信号所表示的瞬时频偏$K_{f}m(t)$，然而噪声的频偏就不好求了。课程中的推导也是通过一些近似的方式得出的，这里就直接给出结果，输出信号功率是$K_f^2{P}_m$（根据调制指数$\beta$的定义可以把$K_f$进行代换），噪声功率最终求出来的近似值为$\frac{2N_0{W}^3}{3A_c^2}$，其中$A_c$是常数表示已调信号$s(t)$的幅值。因此，输出信噪比为：

$\gamma =\frac{3K_f^2{P}_m{A}_c^2}{2N_0{W}^3}$
$将\beta =\frac{\Delta f_{\max }}{W}=\frac{K_f|m(t){|}_{\max }}{W}代入得$
$=\frac{3{\beta }^2{P}_m{A}_c^2}{|m(t){|}_{\max }^{2}2N_{0}W}$
$根据接收信号功率P_R=P_s=A_c^2/2整理上式得$
$=\frac{3{\beta }^2{P}_m{P}_R}{|m(t){|}_{\max }{N}_{0}W}$

其中，$\frac{|m(t){|}_{\max }}{P_m}$称为峰均比，即峰值瞬时功率与平均功率的比值。从上式可以看出，调制指数与输出信噪比成正比，调制信号峰均比与输出信噪比成反比。

---

总结

角度调制系统为非线性系统，处理推导过程不像之前幅度调制那么方便，有许多工程上的近似，前提假设等。增大调制指数可以有效提高输出信噪比，但是由卡松公式可知相应的带宽也会增加。在通信原理中有许多这样的互相制约的量，想要优化其中一个量就会牺牲另一量。这一节的话输出信噪比的结果是需要掌握的，推导过程一般不会有要求。