【回溯】Leetcode 51. N 皇后【困难】-编程知识

【回溯】Leetcode 51. N 皇后【困难】

N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例1：
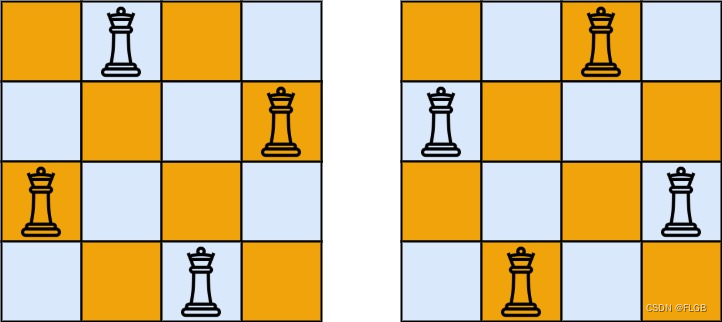
在这里插入图片描述
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

解题思路

1、使用回溯算法来生成所有不同的N皇后问题的解决方案。
2、在每一行中，依次尝试放置皇后，并检查是否符合规则，即不在同一行、同一列、同一对角线上。
3、使用递归回溯的方法，尝试放置皇后，并继续向下一行递归放置。
4、如果当前行放置皇后后，无法找到合适的位置，则回溯到上一行重新尝试。

解题步骤

1、初始化棋盘：创建一个大小为 n×n 的棋盘，用二维数组表示，初始时所有位置都为空（用 ‘.’ 表示）。
2、回溯搜索：从第一行开始逐行放置皇后，在放置每一行的皇后时，都需要检查当前位置是否合法。
如果合法，则将皇后放置在该位置，并继续递归地放置下一行的皇后；
如果不合法，则尝试下一个位置。在递归的过程中，需要记录已经放置的皇后的位置，以便进行回溯。
3、递归结束条件：当放置了所有的皇后时，即递归到达了棋盘的最后一行，
此时找到了一个可行解，将该解保存下来。然后回溯到上一行，尝试放置下一个皇后，继续搜索其他解。
4、合法性检查：在放置皇后时，需要检查当前位置是否与已放置的皇后冲突。
具体地，需要检查当前位置的同一列、同一行、左上对角线和右上对角线是否已经存在皇后。如果存在冲突，则当前位置不合法，需要尝试下一个位置。
5、保存解：当找到一个合法的解时，将该解保存到结果集中，
并继续搜索其他可能的解。
6、回溯：在搜索过程中，如果发现当前位置无法放置皇后，或者已经找到了一个解，
则需要回溯到上一步，撤销当前操作，尝试其他可能的选择。
7、返回结果：当搜索结束时，返回所有找到的合法解。

java实现

public class NQueens {public List<List<String>> solveNQueens(int n) {//保存结果集List<List<String>> result = new ArrayList<>();//初始化棋盘char[][] board = new char[n][n];for (int i = 0; i < n; i++) {Arrays.fill(board[i], '.');}//放置皇后backtrack(result, board, 0);return result;}//回溯private void backtrack(List<List<String>> result, char[][] board, int row) {if (row == board.length) {result.add(constructSolution(board));return;}for (int col = 0; col < board.length; col++) {///判断放置位置是否符合规则if (isValid(board, row, col)) {board[row][col] = 'Q';backtrack(result, board, row + 1);//撤销此次产生的影响,回溯到上一步board[row][col] = '.';}}}//判断放置位置是否符合规则private boolean isValid(char[][] board, int row, int col) {for (int i = 0; i < row; i++) {// 检查列是否有皇后冲突if (board[i][col] == 'Q') return false;//获取行的差值，用于下面左上方、右上方对角线对应的位置//对于[row][col]因i= row-d 转换成[i+d,col]，所以[i,col-d]一定在其左上方// 随着i从0到row变化，d的值也在改变，d=1，board[i][col - d]就是[row][col]左上方的格子，// d=2，board[i][col - d]就是[row][col]左上方的左上方的格子int d = row - i;// 检查左上方对角线是否有皇后冲突if (col - d >= 0 && board[i][col - d] == 'Q') return false;// 检查右上方对角线是否有皇后冲突if (col + d < board.length && board[i][col + d] == 'Q') return false;}return true;}//记录解决方案private List<String> constructSolution(char[][] board) {List<String> solution = new ArrayList<>();for (char[] row : board) {solution.add(String.valueOf(row));}return solution;}public static void main(String[] args) {NQueens nQueens = new NQueens();List<List<String>> solutions = nQueens.solveNQueens(4);for (List<String> solution : solutions) {for (String row : solution) {System.out.println(row);}System.out.println();}}
}