题目一：递归计算斐波那契数

斐波那契数的定义

斐波那契数，也被称为斐波那契数列。每一项数字都是前两项数字的和。斐波那契数列从 1 开始。例如，前10个斐波那契数为1、1、2、3、5、8、13、21、34、55。

代码

int Fact(int n)
{if (n == 1 || n == 2)//递归停止条件return 1;elsereturn Fact(n - 1) + Fact(n - 2);//不断趋近递归停止条件
}
int main()
{int n = 0;int res = 0;//最终结果resultprintf("请问你要求第几个斐波那契数：");scanf("%d", &n);res = Fact(n);//调用Fact函数，并把返回值赋给resprintf("第%d个斐波那契数为%d\n", n, res);return 0;
}

运行截图

递归过程

int Fact(int n)
{if (n == 1 || n == 2)//递归停止条件return 1;elsereturn Fact(n - 1) + Fact(n - 2);//不断趋近递归停止条件
}

以n=5为例：

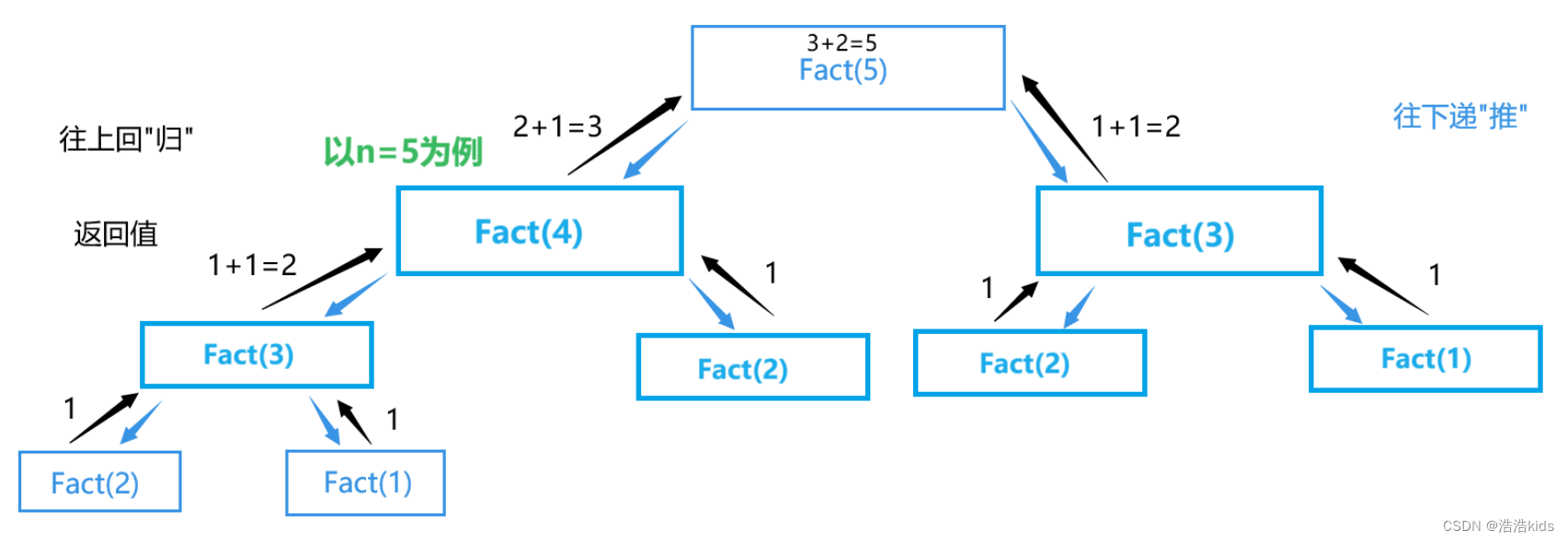
递归停止条件（1个参数）✨

int Fact(int n)
{if (n == 1 || n == 2)//递归停止条件return 1;elsereturn Fact(n - 1) + Fact(n - 2);//不断趋近递归停止条件
}

可以发现if (n == 1 || n == 2)//递归停止条件和return Fact(n - 1) + Fact(n - 2);//不断趋近递归停止条件 中都含有n。在递归中使这个相同的字母不断变化，逐渐趋向某个特定的值，当等于那个特定值时就停止递归。

递归必须是有限的，递归层次太深可能会导致栈溢出。

栈溢出是因为同时占用了太多空间，如果释放空间足够及时就不会溢出。

上述题目用递归实现，如果要计算的斐波那契数 太靠后，比如 第50位 斐波那契数，运行时间会很长。这个题目用递归实现的效率其实比较低，因为除了Fact(1)和Fact(2)，其他Fact()都需要往下递归两个Fact()才能返回当前结果。

这里主要是学习递归的思想。

所以不是所有情况都适合使用递归，“递归虽好，但不要滥用哦”。

非递归实现方法

//非递归
int main()
{int n = 0;int res = 0;int a = 1;//第一个加数int b = 1;//第二个加数scanf("%d", &n);if (n == 1 || n == 2)res = 1;elsefor(int i = n - 2;i > 0;i--){res = a + b;a = b;//a的赋值必须在b的前，因为程序从下往上执行，a需要被更新为之前的bb = res;//b的赋值}printf("第%d个斐波那契数为%d\n", n, res);return 0;
}

题目二：递归实现n的k次方

例如2的3次方为8，3的2次方为9。

代码

int Fact(int n,int k)
{//1的多少次方都为1if (n == 1)return 1;//n不为1的情况if (k == 0)//递归停止条件return 1;elsereturn n*Fact(n,(k - 1));//不断趋向递归停止条件
}
int main()
{int n = 0;//底数int res = 0;//最终结果resultint k = 0;//指数printf("请分别输入n和k：");scanf("%d %d", &n,&k);res = Fact(n,k);//调用函数Fact，并把返回值赋给resprintf("%d的%d次方为%d\n", n, k, res);return 0;
}

运行截图

递归过程

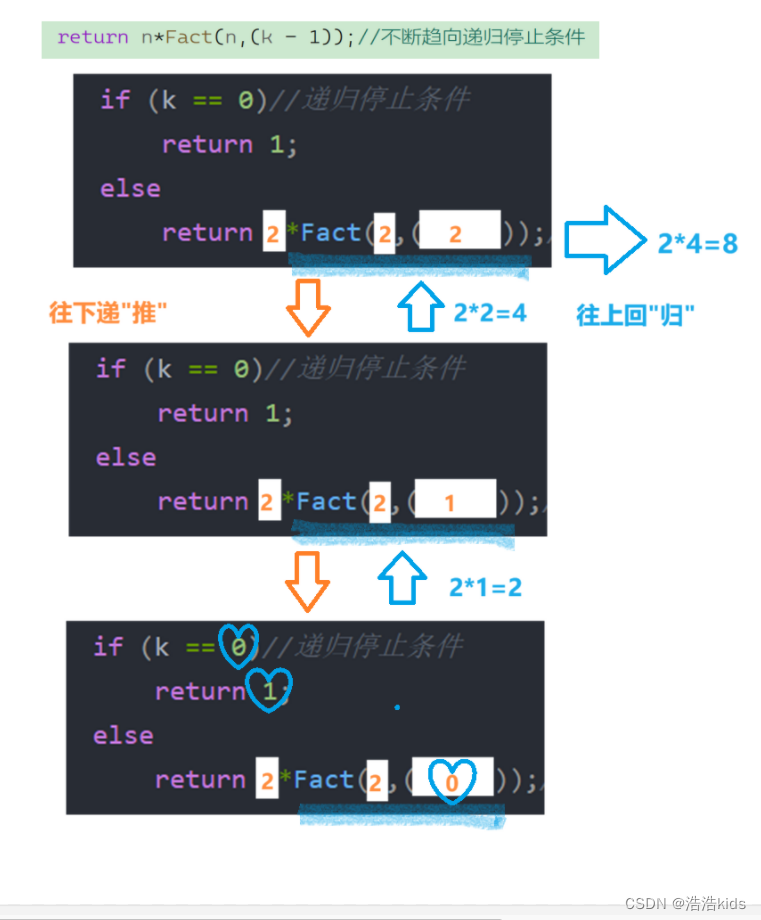
递归停止条件（不止1个参数）✨

只需要关注递归过程中变化的参数。 如果想不明白，可以想想非递归是如何实现的。

int res = 1;
for (int i = 0; i < k; i++)
{res *= n;
}

非递归就是循环，也叫做“迭代”。

加油🎉

正因为你有能力跨越，这个考验才会降临。❤️
你又向目标迈进了哦！

❤️❤️❤️ 恭喜! 恭喜! 又收了两名小弟! ❤️❤️❤️