目录
前言
单向广度优先搜索
双向广度优先搜索
前言
题目链接:单词演变
题目:
输入两个长度相同但内容不同的单词(beginWord 和 endWord)和一个单词列表(wordList),求从 beginWord 到 endWord 的演变序列的最短长度,要求每步只能改变单词中的一个字母,并且演变过程中每步得到的单词都必须在给定的单词列表中。如果不能从 beginWord 演变到 endWord,则返回 0。假设所有单词只包含英文小写字母。
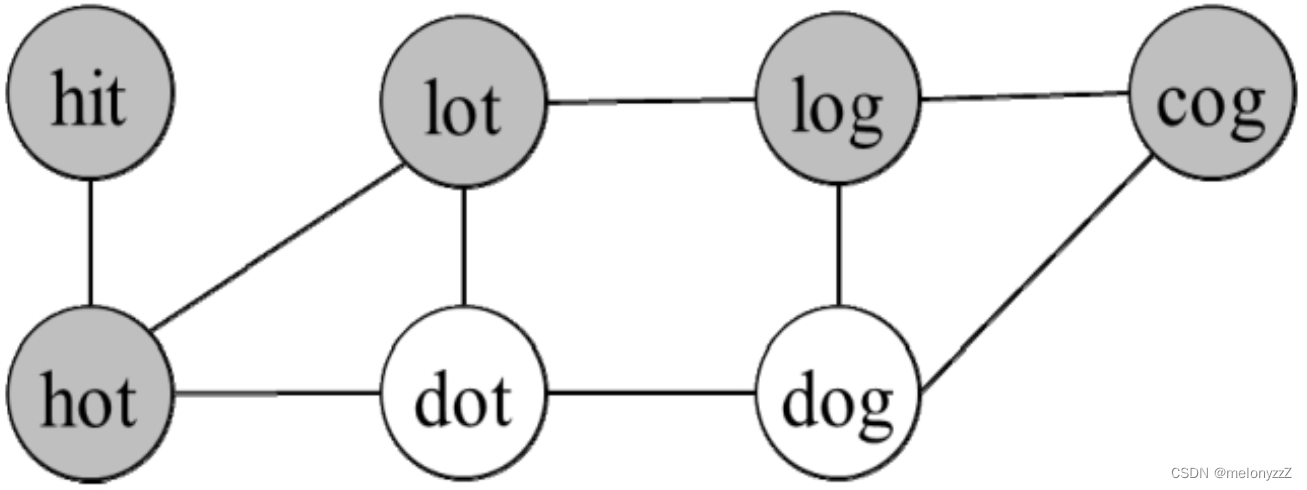
例如,如果 beginWord 为 "hit",endWord 为 "cog",wordList 为 ["hot", "dot", "dog", "lot", "log", "cog"],则演变序列的最短长度为 5,一个可行的演变序列为 "hit"->"hot"->"dot"->"dog"->"cog"。
分析:
应用图相关算法的前提是找出图中的节点和边。这个问题是关于单词的演变的,所以每个单词就是图中的一个节点。如果两个单词能够相互演变(改变一个单词的一个字母就能变成另一个单词),那么这两个单词之间有一条边相连。例如,可以用下图表示 "hit"、"hot"、"dot"、"dog"、"lot"、"log"、"cog" 的演变关系,可以看出,从 "hit" 演变成 "cog" 的最短序列的长度为 5,一个可行的最短序列经过的节点用阴影表示。
单向广度优先搜索
这个题目要求计算最短演变序列的长度,即求图中两个节点的最短距离。表示单词演变的图也是一个无权图,按照题目的要求,图中两个节点的距离是连通两个节点的路径经过的节点的数目。通常用广度优先搜索计算无权图中的最短路径,广度优先搜索通常需要用到队列。
为了求得两个节点之间的最短距离,常见的解法是用两个队列实现广度优先搜索算法。一个队列 q1 中存放离起始节点距离为 d 的节点,当从这个队列中取出节点并访问的时候,与队列 q1 中相邻的节点离起始节点的距离都是 d + 1,将这些相邻的节点存放到另一个队列 q2 中。当队列 q1 中的所有节点都访问完毕时,再访问队列 q2 中的节点,并将相邻的节点放入 q1 中。可以交替使用 q1 和 q2 这两个队列由近及远地从起始节点开始搜索所有节点。
class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> notVisited(wordList.begin(), wordList.end());queue<string> q1, q2;q1.push(beginWord);int length = 1;while (!q1.empty()){string word = q1.front();q1.pop();if (word == endWord)return length;vector<string> neighbors = getNeighbors(word);for (string& neighbor : neighbors){if (notVisited.count(neighbor)){q2.push(neighbor);notVisited.erase(neighbor);}}
if (q1.empty()){q1 = q2;q2 = queue<string>();++length;}}return 0;}
private:vector<string> getNeighbors(string& word) {vector<string> neighbors;for (int i = 0; i < word.size(); ++i){char old = word[i];for (char ch = 'a'; ch <= 'z'; ++ch){if (ch != old){word[i] = ch;neighbors.push_back(word);}}word[i] = old;}return neighbors;}
};上述代码首先将起始节点 beginWord 添加到队列 q1 中。接下来每一步从队列 q1 中取出一个节点 word 访问。如果 word 就是目标节点,则搜索结束;否则找出所有与 word 相邻的节点并将相邻的节点放到队列 q2 中。当队列 q1 中的所有节点都访问完毕时交换队列 q1 和 q2,以便接下来访问原来存放在队列 q2 中的节点。每次交换队列 q1 和 q2 都意味着距离初始结点距离为 d 的节点都访问完毕,接下来将访问距离为 d + 1 的节点,因此距离值增加 1。
上述代码将单词列表中还没有访问过的节点放入 notVisited 中,每当一个单词被访问过就从这个 unordered_set 中删除。如果一个节点不在 notVisited 中,要么它不在单词列表之中,要么之前已经访问过,不管是哪种情况这个节点都可以忽略。
双向广度优先搜索
这个题目是关于单一起始节点、单一目标节点的最短距离问题。前面的解法是从起始节点出发不断朝着目标节点的方向搜索,直到到达目标节点。针对这类问题有一种常用的优化方法,即在从起始节点出发不断朝着目标节点的方向搜索的同时,也从目标节点出发不断朝着起始节点的方向搜索。这种双向搜索的方法能够缩小搜索空间,从而提高搜索效率。
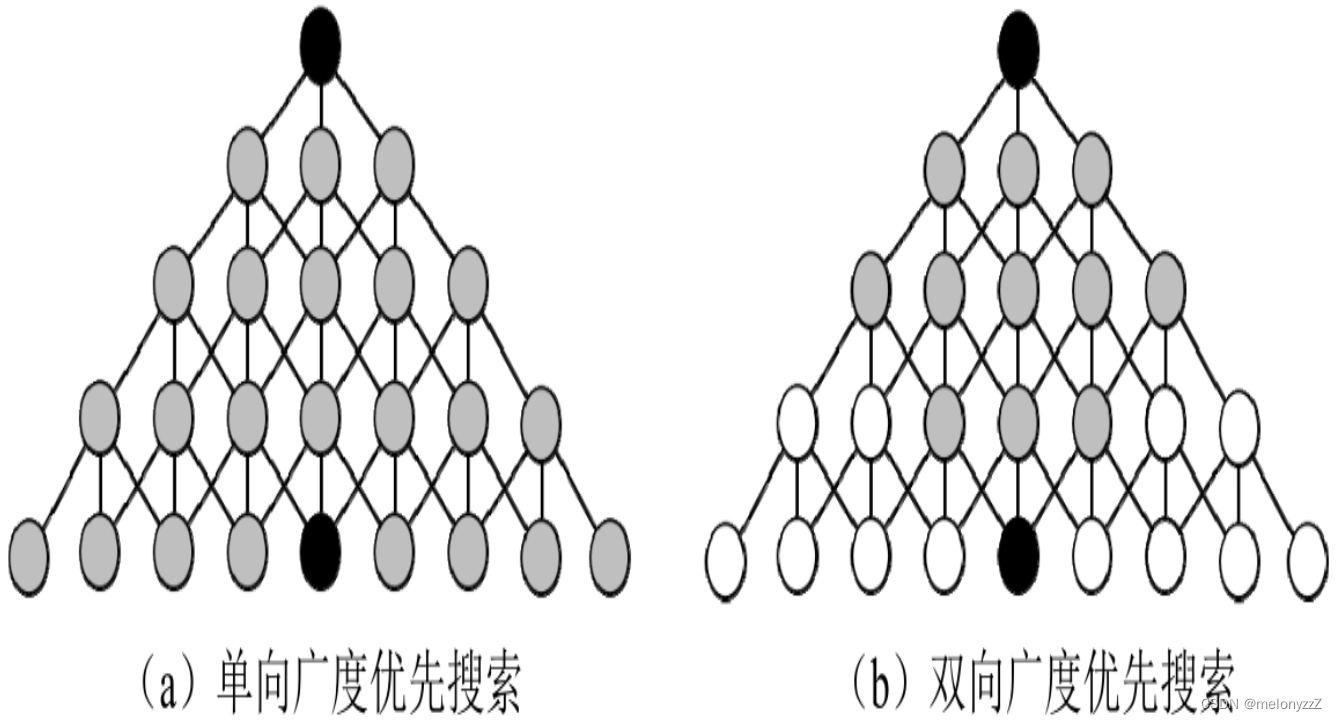
下图是双向广度优先搜索缩小搜索空间的示意图。假设目标是求出图中顶部的黑色节点到底部的黑色节点的最短距离。如果采用广度优先搜索,那么图中所有节点都可能会被搜索到,如下图 (a) 所示。如果采用双向广度优先搜索,则分别从起始节点和目标节点出发不断搜索,直到在中间某个位置相遇,那么图中只有部分节点被搜索到,如下图 (b) 所示。
class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> notVisited(wordList.begin(), wordList.end());if (notVisited.count(endWord) == 0)return 0;unordered_set<string> s1, s2;s1.insert(beginWord), s2.insert(endWord);int length = 2;while (!s1.empty() && !s2.empty()){if (s2.size() < s1.size())s1.swap(s2);unordered_set<string> s3;for (const string& word : s1){vector<string> neighbors = getNeighbors(word);for (string& neighbor : neighbors){if (s2.count(neighbor))return length;if (notVisited.count(neighbor)){s3.insert(neighbor);notVisited.erase(neighbor);}}}++length;s1 = s3;}return 0;}
private:vector<string> getNeighbors(const string& word) {string tmp = word;vector<string> neighbors;for (int i = 0; i < tmp.size(); ++i){char old = tmp[i];for (char ch = 'a'; ch <= 'z'; ++ch){if (ch != old){tmp[i] = ch;neighbors.push_back(tmp);}}tmp[i] = old;}return neighbors;}
};在上述代码中,s1 和 s2 分别存放两个方向上当前需要访问的节点,s3 用来存放与当前访问的节点相邻的节点。之所以这里用的是 unordered_set 而不是 queue,是因为需要判断从一个方向搜索到的节点在另一个方向是否已经访问过。只需要 O(1) 的时间就能判断 unordered_set 中是否包含一个元素。
先将起始节点 beginWord 添加到 s1 中,将目标节点 endWord 添加到 s2 中。接下来每次 while 循环都是从需要访问的节点数目少的方向搜索,这样做是为了缩小搜索的空间。先确保 s1 中需要访问的节点数更少,接下来访问 s1 中的每个节点 word。如果某个与节点 word 相邻的节点 neighbor 在 s2 中,则说明两个不同方向的搜索相遇,已经找到了一条起始节点和目标节点之间的最短路径,此时路径的长度就是它们之间的最短距离,否则将节点 neighbor 添加到 s3 中。当 s1 中所有的节点都访问完毕,接下来可能会访问 s1 的节点的相邻节点,即 s3 中的节点,因此将 s1 指向 s3。然后继续从 s1 和 s2 中选择一个节点数目少的方向进行新一轮的搜索。每轮搜索都意味着在起始节点和目标节点之间的最短路径上多前进了一步,因此变量 length 增加 1。