机器学习周记（第三十四周：文献阅读[GNet-LS]）2024.4.8~2024.4.14-编程知识

摘要

ABSTRACT

1 论文信息

1.1 论文标题

1.2 论文摘要

1.3 论文模型

1.3.1 数据处理

1.3.2 GNet-LS

2 相关代码

摘要

本周阅读了一篇时间序列预测论文。论文模型为GNet-LS，主要包含四个模块：粒度划分模块（GD），变量间外部关系挖掘模块（ER），目标变量内部关系挖掘模块（IC），特征融合模块（DF）。首先，通过粒度划分模块将原始多元时间序列序列划分为多粒度序列，接着由变量间外部关系挖掘模块捕获外部关系，目标变量内部关系挖掘模块挖掘内部相关性，最后通过数据融合模块获得最终的预测结果。GNet-LS主要由CNN、LSTM、Attention、自回归组成。

ABSTRACT

This week, We read a paper on time series forecasting. The paper presents a model called GNet-LS, which consists of four main modules: Granularity Division (GD), External Relationship Mining between Variables (ER), Internal Correlation Mining of the Target Variable (IC), and Data Fusion (DF). First, the original multivariate time series is divided into multi-granularity sequences through the Granularity Division module. Then, the External Relationship Mining module captures external relationships, the Internal Correlation Mining module explores internal correlations, and finally, the Data Fusion module produces the final prediction result. GNet-LS mainly comprises CNNs, LSTMs, Attention mechanisms, and autoregressive components.

1 论文信息

1.1 论文标题

1.2 论文摘要

多元时间序列预测是经济学、金融学和交通运输等多个领域中的一个重要研究问题，这些领域需要同时进行长期和短期预测。然而，当前的技术通常仅限于单一的短期或长期预测。为了解决这一限制，本文提出了一种新颖的多粒度层次网络GNet-LS，用于多元时间序列数据的长短期预测，该网络考虑了内部相关性和外部关系的独立作用。首先，基于下采样将原始时间序列序列划分为多个粒度序列，以减少由长期预测引起的误差累积。为了发现变量之间的外部关系，卷积神经网络（CNN）模块在变量序列上滑动。构建全局CNN和局部CNN分别实现周期性和非周期性提取。接着，使用自注意力模块模拟局部CNN和全局CNN输出之间的依赖关系。长短时记忆网络（LSTM）和注意力机制用于挖掘时间序列目标变量的内部相关性。然后，以并行方式获得多粒度的外部关系和内部相关性。最后，通过拼接和叠加融合外部关系和内部相关性，以获得长期和短期预测。实验结果表明，所提出的GNet-LS在RSE、CORR、MAE和RMSE等方面优于一系列比较方法。

1.3 论文模型

1.3.1 数据处理

给定时间序列 $X^{d}=\left \langle x_{1}^{d},...,x_{t}^{d},...,x_{T}^{d} \right \rangle$ 是观测到的按时间顺序排列的测量值序列，其中 $x_{t}^{d}$ 表示变量 $d$ 在时间点 $t$ 处的值，两个连续测量值之间的时间间隔通常是常数， $T$ 表示变量 $X^{(d)}$ 的长度。多元时间序列记为 $X=\left \langle X^{1},...,X^{d},...,X^{D} \right \rangle$ ， $X$ 中的序列是相互关联的， $D$ 表示多元时间序列数据 $X$ 中的变量个数。

多粒度表示：不同的时间粒度以多种方式描述。它可以被划分为年、月、日、小时、分钟乃至秒。因为不同的场景需要不同的时间粒度，所以为了充分分析预测任务的准确，适当的粒度至关重要。在不失一般性的前提下，可以首先给出单变量时间序列的粒度描述。对于给定的变量 $X^{(d)}$ ， $X^{(d)}=\left \langle x_{1}^{(d)},...,x_{t}^{(d)},...,x_{T}^{(d)} \right \rangle$ 的时间序列，将这个原始序列的粒度设置为 $g_{0}$ ，记作 $g_{0}(X^{(d)})=\left \langle x_{1}^{(d)},...,x_{t}^{(d)},...,x_{T}^{(d)} \right \rangle$ 。

在本文中利用降采样方法呈现了从精细到粗糙的原始序列。也就是说，将原始序列按照降采样频率 $k_{1}<k_{2}<\cdot \cdot \cdot <k_{n}$ 划分为 $n$ 个粒度，分别表示为 $g_{1},g_{2},\cdot \cdot \cdot ,g_{n}$ 。这里 $g_{1}(X^{(d)})=\left \langle x_{1}^{(d)},...,x_{1+k_{1}}^{(d)},...,x_{T_{k_{1}}}^{(d)} \right \rangle$ ， $g_{n}(X^{(d)})=\left \langle x_{1}^{(d)},...,x_{1+k_{n}}^{(d)},...,x_{T_{k_{n}}}^{(d)} \right \rangle$ ， $k_{n}$ 表示降采样频率， $g_{n}(X^{(d)})$ 是具有频率 $k_{n}$ 的结果。然后，得到了原始时间序列数据的 $n+1$ 个粒度的数量，表示为 $G(X^{(d)})=\left \langle g_{0}(X^{(d)},g_{1}(X^{(d)},...,g_{s}(X^{(d)},...,g_{n}(X^{(d)}) \right \rangle s\in [1,n]$ 。

对于多元时间序列数据，可以将每个变量视为单变量时间序列。因此，同样可以得到多变量时间序列数据的多粒度表示，表示为 $G(X)=\left \langle g_{0}(X),g_{1}(X),g_{2}(X),...,g_{n}(X) \right \rangle$ 。

问题定义：给定一组多元时间序列 $X=\left \langle X^{(1)},...,X^{(d)},...,X^{(D)} \right \rangle$ ，其中 $D$ 是变量数量， $X^{(D)} \in R^{T}$ 表示第 $D$ 个变量具有 $T$ 个时间点的序列。首先对多元时间序列数据进行降采样，并且主要以滚动预测的方式进行预测。也就是说，基于过去时间序列 $\left \langle X_{1},X_{t},...,X_{T} \right \rangle$ 预测未来目标值 $X_{T+h}$ ，其中 $h$ 是当前时间段可以预测的理想步长。 $X_{t}$ 表示在时间 $t$ 时 $D$ 个变量的取值，因此 $X_{t} \in R^{D}$ 。同样地，可以试图基于 $\left \langle X_{1},X_{t},...,X_{T} \right \rangle$ 预测未来目标值 $X_{T+h+p}$ ，其中 $p$ 是可以在相同准确度下预测更长时间距离的理想步长。当然， $p$ 越大，模型在更长的步长上的表现就越好。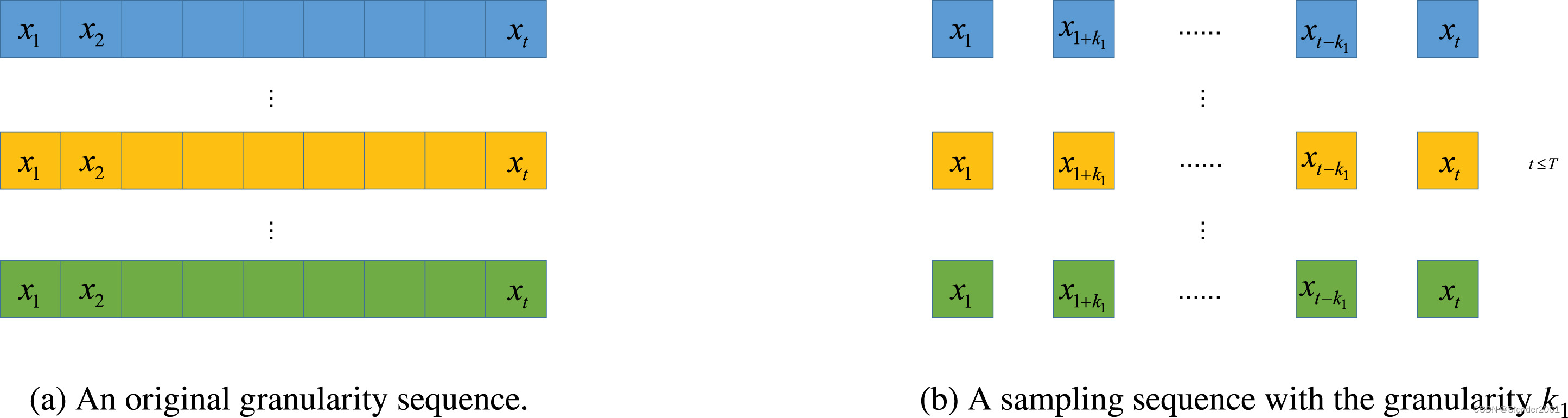 $X=\left \langle X^{(1)},...,X^{(d)},...,X^{(D)} \right \rangle \in R^{T \times D}$ 代表了具有 $D$ 个变量和 $T$ 个时间步长的多元时间序列预测数据。多元时间序列数据的一个示例，即原始粒度序列，如Fig.1(a)所示。在粒度为 $k_{n}$ 的采样后的粒度序列如Fig.1(b)所示。

1.3.2 GNet-LS

GNet-LS包括四个模块，如Fig.2所示。首先，通过粒度划分模块将原始多元时间序列序列划分为多粒度序列，该模块简称为GD模块（粒度划分模块）。接下来，通过处理原始序列 $g_{0}(X)$ ，由变量间外部关系挖掘模块（简称ER模块）捕获外部关系。同时，通过处理多粒度序列如 $g_{1}(X)$ 、 $g_{2}(X)$ 等等，目标变量内部关系挖掘模块（简称IC模块）挖掘内部相关性。然后，通过数据融合模块（简称DF模块）获得最终的预测结果。

GNet-LS的总体概述如Fig.2所示。该图显示了论文所提出的模型从原始数据输入至粒度划分模块为起始，其中原始数据由频率采样机制进行粒度化，然后不同粒度的数据输入到后续的预测模块。也就是说，数据 $g_{1}(X)$ 和 $g_{2}(X)$ 由IC模块并行处理。最后，DF模块输出预测结果。

粒度划分模块（GD）：不同时间粒度的数据反映的信息变化趋势不同。细粒度的时间序列可以保留更详细的信息，而大粒度的时间序列可以捕捉长期变化的趋势。因此，文中尝试从粒计算的角度将原始粒度数据划分为多粒度数据，进而从不同粒度序列中发现多元变量之间复杂的动态关系。

一般来说，我们获得的原始多元时间序列数据是单粒度数据。为此，文中引入了降采样方法，对原始数据按特定频率进行采样，以从原始数据中提取出更细粒度的时间序列。一个例子如Fig.3所示。

设置多少粒度仍然是一个具有挑战性的问题，可以作为未来的研究。论文主要证明的是多粒度思维是先进的。因此，在论文设计的模型中，模型的粒度简单地被设置为3。即原始序列 $g_{0}(X)$ ，两个子粒度序列 $g_{1}(X)$ 和 $g_{2}(X)$ ，分别按下采样频率 $k_{1}$ 、 $k_{2}$ 对粒度序列进行采样。如果输入的时间序列是 $X \in R^{D \times T}$ ，那么可以定义如下三种粒度序列：

$g_{0}(X)=\left \langle X_{1},X_{2},...,X_{T} \right \rangle$ (1)

$g_{1}(X)=\left \langle X_{1},X_{1+k_{1}},...,X_{T_{k1}} \right \rangle$ (2)

$g_{2}(X)=\left \langle X_{1},X_{1+k_{2}},...,X_{T_{k2}} \right \rangle$ (3)

通过采样，可以试图恢复原始序列中的一些周期特性。利用划分后的粒度序列挖掘长期预测中变化的底层模式。这种多频率采样周期挖掘方法有望显著降低步长累积效应的预测误差，并希望不同粒度的序列能够对不同的预测步骤起到不同的支持作用。

窗口滑动技术是处理多元时间序列的常用技术。在这项工作中，每个粒度序列相应地固定一个计算窗口的尺寸。对于上面的粒度划分公式，需要注意 $T_{k1}$ 和 $T_{k2}$ 比 $T$ 小，因为需要确保滑动窗口中的粒度划分。然后，随着窗口的移动，窗口中的数据将发生变化，模型将使用不同的数据进行训练。

变量间外部关系挖掘模块（ER）：卷积神经网络的成功很大程度上依赖于其捕捉必要信号的能力。这一特性使得卷积神经网络（CNN）特别适用于序列预测。因此，在本文中，主要介绍CNN用于特征提取。由于数据集多样性，一些数据集具有明显的周期性，而另一些则没有明显周期性。为了使模型更好地适应这两种情况，论文计划设计全局CNN和局部CNN共同工作。

多个 $n_{G}$ filters协同构成全局CNN（G-CNN）。每个filter将扫描一次变量，因此每次扫描后将生成一个 $D \times 1$ 向量。由于有 $n_{G}$ 个filter，每个filter扫描一次输入，当所有filter扫描完成后，将生成一个 $D \times n_{G}$ 矩阵。所使用的激活函数是ReLU函数。向量的每一行可以被视为单个变量的学习表示，然后通过随后的多头注意力机制，学习所有特征，并为后续预测做出更好的决策。

局部CNN（L-CNN）采取与全局CNN相似的方法。L-CNN专注于建立局部时间模式。局部时间卷积核使用长度为 $l$ 的filter，超参数 $l<T$ 。局部卷积核通过滑动方法提取信息。例如，对于步长为 $T$ 的时间序列，创建一个长度为 $T-l+1$ 的向量。为了将每个特征时间关系映射到一个向量表示，论文使用一维最大池化层在序列的每个滑动步骤后捕获最具代表性的特征，池化层的大小为 $T-l+1$ 。最后，产生一个 $D \times n_{L}$ 矩阵，其中 $n_{L}$ 是局部卷积核中的filter数量。局部卷积神经网络的过程如Fig.4(a)所示。

为了捕捉不同序列之间的关系，对于每个特征变量，模型分别使用自注意力机制学习，因为其具有强大的特征提取能力。然后，模型通过多头注意力机制学习自身与其他序列之间的关系。自注意力机制的组成如Fig.4(b)所示。

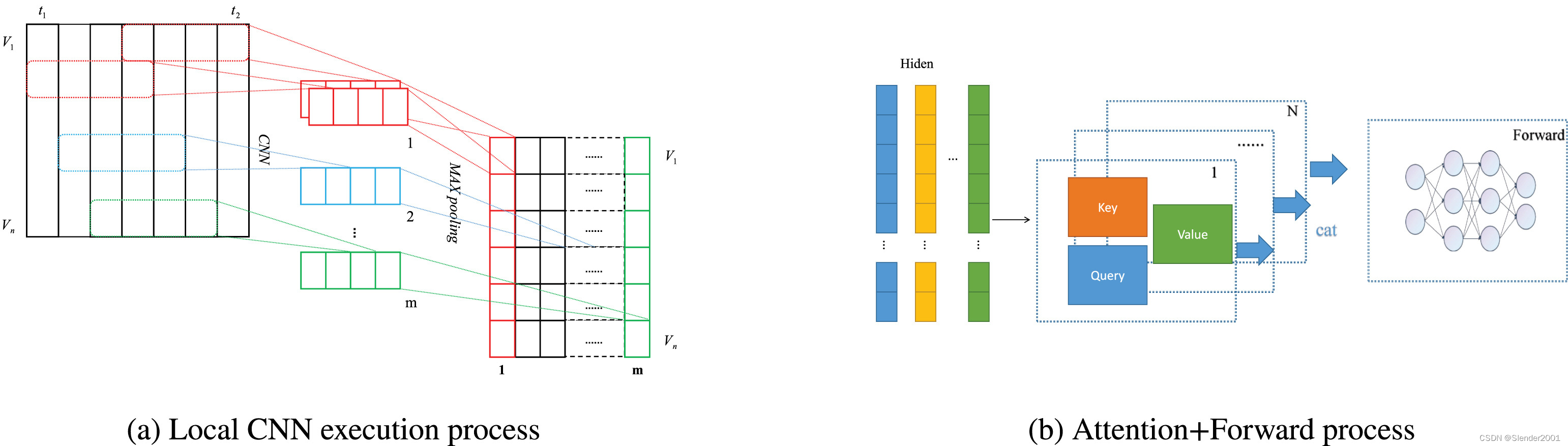
将全局卷积神经网络（G-CNNs）和局部卷积神经网络（L-CNNs）的输出作为注意力处理的输入，然后将结果显示为Query、Key和Value向量。接着，通过加权，创建了一个具有特定权重关系的输出，这可以被理解为更加关注有用的信息。每个点的权重是通过计算时间序列中其他点的Query与当前点的Key的内积来计算的，然后将Value乘以内积后继续向前处理，以获得当前模块的输出。Query、Key和Value之间的关系如下：

$Z = softmax(\frac{Q(K)^{T}}{\sqrt{d}})V$ (4)

其中 $d$ 是key的维度。使用多头注意力机制允许模型共同处理来自不同表示的信息，这些信息被串联起来并线性投影以获得最终的表示 $Z$ 。

逐位置前馈层由两个线性变换组成，在它们之间有一个 $\textup{ReLU}$ 激活函数，可以表示为：

$h_{t}^{O}=ReLU(ZW_{1}+b_{1})W_{2}+b_{2}$ (5)

虽然线性变换在不同位置是相同的，但它们使用不同的参数。每个子层周围的层归一化和残差连接使得训练更容易并且提高泛化性能。无论是在G-CNNs还是L-CNNs中都有上述过程，即通过将 $Z$ 输入到模块中获得最终的 $h_{t}^{O}$ 。

目标变量内部关系挖掘模块（IC）：长短期记忆网络（LSTM）是一种用于深度学习的人工递归神经网络，能够处理单个数据点或一系列段落。此处引入LSTM的主要目的是推导时间序列的预测结果 $h_{t}$ 及其对应的隐藏状态。然后，根据对应的隐藏状态，计算其与前一个时间窗口隐藏层之间的权重，并用于校正特征权重矩阵，以捕获更多有用的特征。在本文中，LSTM用于预测不同粒度的频率序列。从原始序列中提取的粒度被输入到LSTM网络中，然后历史数据由注意力网络识别，该网络能够突出历史序列对后续结果的影响。使用LSTM网络允许从原始数据中分析历史时间点和周期性质，并对发现的内部相关性进行建模，使最终结果更加准确。

首先，对于输入矩阵向量，使用LSTM模型接收所有输入值，然后获得隐藏层信息 $h_{1:T}=[h_{1},...,h_{T}]$ 。之后，预测未来时序向量信息 $h_{T:T+h}=[h_{T},...,h_{T+h}]$ ，最后将它为输入注意力网络分析时序向量关系。

准确的时间预测不仅需要模型能够精确控制外部关系，还需要对数据的内部相关性进行合理分析。本文使用一组长短期记忆网络（LSTMs）层来分析粒度数据。与以前的模型不同，LSTMs并行工作。同时，将卷积神经网络（CNNs）和LSTMs分别学习，以便充分利用每个模型的最佳可能结果，然后进行后续的预测任务。对于长短期记忆网络组件，使用传统的LSTM网络，该网络学习数据的不同周期性，然后这里的输入是具有一定时间间隔的时间序列。传统的LSTM利用相邻的 $X_{t}:X_{t+1}$ 作为模型输入。论文将其输入调整为 $X_{t}:X_{t+k}$ ，以学习不同周期性的关系。此处， $k$ 是不同周期的粒度， $k$ 的值根据不同的任务场景和数据集而变化，而合理的 $k$ 值将对结果有正相关影响。本文根据 $k$ 选择不同的隐藏层，选定的隐藏层肯定是单一时间序列结果。为了使最终结果包含更好的记忆特性，增加了一个注意力层，它选择对当前影响最大的历史数据的时间序列。实现过程如下方程所示：

$H_{t},c_{t}=F(h_{t-1-k},c_{t-1-k},x_{t})$ (6)

$O_{w}=\textup{tahh}(H \times w_{w})$ (7)

$h_{t}^{G}=X_{T+h}=sum(X \times attscore)$ $attscore = softmax(O_{w} \times w_{o})$ (8)

符号 $H_{t}$ 代表模型LSTM为后续预测任务输出的结果。 $w_{w} \in R^{h \times h}$ 代表第一阶段的权重值， $h_{t-1}$ 是所表示的LSTM模型的隐藏层维度。第一阶段的权重分配通过矩阵乘法执行，并最终在tanh操作后获得第一阶段的记忆结果。其中 $O_{w} \in R^{n \times h}$ 是滑动窗口中 $n$ 值对应的粒度数据的次数， $O_{w}$ 与 $w_{0}$ 矩阵相乘，得到第二阶段的权重分配。通过softmax函数获得最终的权重得分 $attscore \in R^{n \times 1}$ ，该权重得分包含对前一个时间点的记忆功能，可以更好地捕捉当前预测时间点的关键时间序列。最终，权重得分被分配到输入时间序列上，并通过求和函数获得最终输出。目标变量挖掘模块的内部相关性处理显示在Algorithm1中。

特征融合模块：在之前几个模块的处理之后，GNet-LS获取了由三个不同粒度序列生成的三个向量。单个向量是某一粒度的结果，不同的结果代表不同的时间模式。问题在于我们如何关联这三个向量并学习它们之间的关系。为了解决这个问题，使用向量和方法将三个向量合并在一起，然后根据反向传播的思想对每个模型进行参数更新。不同的预测任务依赖于不同的序列。例如，较长的预测任务依赖于较粗的时间序列，较短的预测任务依赖于较细的时间序列。

卷积神经网络（CNNs）和递归神经网络（RNNs）更关注组件的非线性特性。为了获得更好的预测结果，GNet-LS结合线性和非线性预测结果。除了上述的非线性组件模块，经典的自回归模型通常被视为线性组件。对于自回归预测结果，可以将其表示为 $h_{t}^{L} \in R^{D}$ ，其中 $D$ 代表变量的数量。然后，根据以下方程，通过线性层和神经网络模块的融合解决方案获得最终的预测结果。

$h_{t}^{L}=\sum_{k=0}^{t-1}W_{k}^{D}X_{t-k}$ (9)

$F(h_{t}^{O},h_{t}^{G_{2}},h_{t}^{L})=X_{t+h}$ (10)

其中 $W_{k}^{D}$ 代表总共 $k$ 组权重，每组的大小为 $D \times 1$ 。这表示每个时间序列 $X_{t}$ 都有一个线性矩阵 $W \in R^{D}$ 。线性矩阵代表序列的权重比例。这里， $h_{t}^{O}$ 、 $h_{t}^{G_{1}}$ 、 $h_{t}^{G_{2}}$ 和 $h_{t}^{L}$ 分别代表来自外部关系模块、 $g_{1}$ 的内部相关模块、 $g_{2}$ 的内部相关模块和线性自回归模块的输出向量。至于 $F$ ，可以理解为一种算术方法，主要使用拼接和叠加方法，当然也可以选择点积、内积等其他方法，通过 $F$ 操作返回最终的预测结果。

2 相关代码

STGNN时间序列预测：

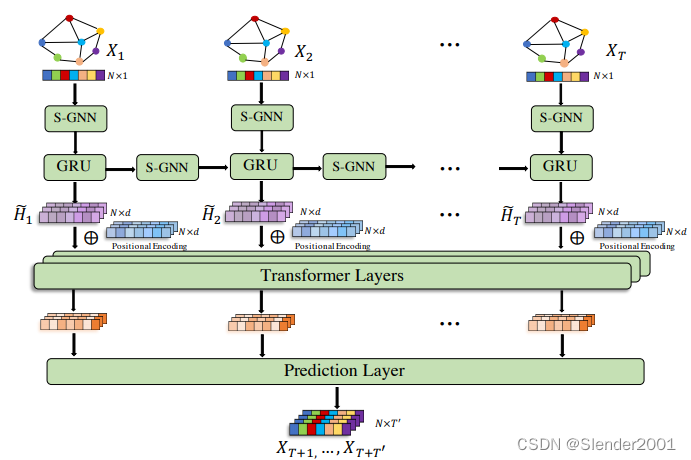
step1：模块定义。包含S-GNN层、GRU层、Transformer层、位置编码。

class Transform(nn.Module):def __init__(self, outfea, d):super(Transform, self).__init__()self.qff = nn.Linear(outfea, outfea)self.kff = nn.Linear(outfea, outfea)self.vff = nn.Linear(outfea, outfea)self.ln = nn.LayerNorm(outfea)self.lnff = nn.LayerNorm(outfea)self.ff = nn.Sequential(nn.Linear(outfea, outfea),nn.ReLU(),nn.Linear(outfea, outfea))self.d = ddef forward(self, x):query = self.qff(x)key = self.kff(x)value = self.vff(x)query = torch.cat(torch.split(query, self.d, -1), 0).permute(0, 2, 1, 3)key = torch.cat(torch.split(key, self.d, -1), 0).permute(0, 2, 3, 1)value = torch.cat(torch.split(value, self.d, -1), 0).permute(0, 2, 1, 3)A = torch.matmul(query, key)A /= (self.d ** 0.5)A = torch.softmax(A, -1)value = torch.matmul(A, value)value = torch.cat(torch.split(value, x.shape[0], 0), -1).permute(0, 2, 1, 3)value += xvalue = self.ln(value)x = self.ff(value) + valuereturn self.lnff(x)class PositionalEncoding(nn.Module):def __init__(self, outfea, max_len):super(PositionalEncoding, self).__init__()# Compute the positional encodings once in log space.pe = torch.zeros(max_len, outfea).to(device)position = torch.arange(0, max_len).unsqueeze(1)div_term = torch.exp(torch.arange(0, outfea, 2) *-(math.log(10000.0) / outfea))pe[:, 0::2] = torch.sin(position * div_term)pe[:, 1::2] = torch.cos(position * div_term)pe = pe.unsqueeze(0).unsqueeze(2)  # [1,T,1,F]self.register_buffer('pe', pe)def forward(self, x):x = x + Variable(self.pe,requires_grad=False)return xclass SGNN(nn.Module):def __init__(self, outfea):super(SGNN, self).__init__()self.ff = nn.Sequential(nn.Linear(outfea, outfea),nn.Linear(outfea, outfea))self.ff1 = nn.Linear(outfea, outfea)def forward(self, x):p = self.ff(x)a = torch.matmul(p, p.transpose(-1, -2))R = torch.relu(torch.softmax(a, -1)) + torch.eye(x.shape[1]).to(device)D = (R.sum(-1) ** -0.5)D[torch.isinf(D)] = 0.D = torch.diag_embed(D)A = torch.matmul(torch.matmul(D, R), D)x = torch.relu(self.ff1(torch.matmul(A, x)))return xclass GRU(nn.Module):def __init__(self, outfea):super(GRU, self).__init__()self.ff = nn.Linear(2 * outfea, 2 * outfea)self.zff = nn.Linear(2 * outfea, outfea)self.outfea = outfeadef forward(self, x, xh):r, u = torch.split(torch.sigmoid(self.ff(torch.cat([x, xh], -1))), self.outfea, -1)z = torch.tanh(self.zff(torch.cat([x, r * xh], -1)))x = u * z + (1 - u) * xhreturn xclass STGNNwithGRU(nn.Module):def __init__(self, outfea, P):super(STGNNwithGRU, self).__init__()self.sgnnh = nn.ModuleList([SGNN(outfea) for i in range(P)])self.sgnnx = nn.ModuleList([SGNN(outfea) for i in range(P)])self.gru = nn.ModuleList([GRU(outfea) for i in range(P)])def forward(self, x):B, T, N, F = x.shapehidden_state = torch.zeros([B, N, F]).to(device)output = []for i in range(T):gx = self.sgnnx[i](x[:, i, :, :])gh = hidden_stateif i != 0:gh = self.sgnnh[i](hidden_state)hidden_state = self.gru[i](gx, gh)output.append(hidden_state)output = torch.stack(output, 1)return output

step2：STGNN模型定义。

class STGNN(nn.Module):def __init__(self, infea, outfea, L, d, P):super(STGNN, self).__init__()self.start_emb = nn.Linear(infea, outfea)self.end_emb = nn.Linear(outfea, infea)self.stgnnwithgru = nn.ModuleList([STGNNwithGRU(outfea, P) for i in range(L)])self.positional_encoding = PositionalEncoding(outfea, P)self.transform = nn.ModuleList([Transform(outfea, d) for i in range(L)])self.L = Ldef forward(self, x):"""x:[B,T,N]"""x = x.unsqueeze(-1)x = self.start_emb(x)for i in range(self.L):x = self.stgnnwithgru[i](x)x = self.positional_encoding(x)for i in range(self.L):x = self.transform[i](x)x = self.end_emb(x)return x.squeeze(-1)