【算法基础2】前缀和与差分-编程知识

前缀和与差分

1.综述

前缀和是某数列的前n项数的和，而差分则可以看做是前缀和的逆运算。前缀和与差分比起是一种算法，更像是一种解决问题的思路，通过构造一个特殊的数组，就可以让我们将某些复杂的问题简化。

2.前缀和

（1）一维前缀和

已知一个数列a[n]，用S[n]来表示这个数列的前n项和数列。
S[i]=a[1]+a[2]+a[3]+…+a[i]
前缀和的用途：当我们要求数列a[n]的[l,r]区间内所有数的和，如果我们用一趟遍历的话，就需要O(n)的时间复杂度，而如果我们利用前缀和数组，就可以将其转化为S[r]-S[l-1]，时间复杂度变成了O(1)。
S[r]=~~a[1]+a[2]+a[3]+…+a[l-1]+~~ a[l]+…+a[r]
S[l-1]=~~a[1]+a[2]+a[3]+…+a[l-1]~~
前缀和数组的预处理时间复杂度仍为O(n)。
这称为一维前缀和。

#include <bits/stdc++.h>using namespace std;const int N=1e6+10;int n,m;
int a[N],s[N];int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];//前缀和的初始化while(m--){int l,r;scanf("%d%d",&l,&r);int res=s[r]-s[l-1];//区间和的计算printf("%d\n",res);    }return 0;
}

（2）二维前缀和（子矩阵的和）

我们将前缀和扩展到二维矩阵中，将前n项的和转化为(x1,y1)坐标与(1,1)组成的矩阵中的所有数的和。而如果我们要求(x1,y1)(x2,y2)之间所有数的和，我们就可以利用前缀和的思路。
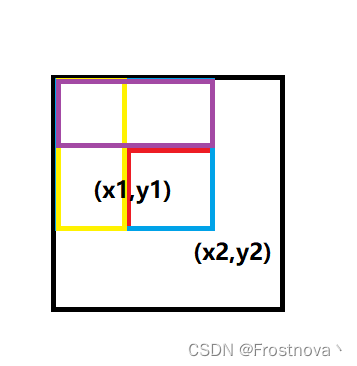
请添加图片描述
如图，将和分为三部分，可得子矩阵的和为
S[x2,y2]-S[x1-1,y2]-S[x2,y1-1]+S[x1-1,y1-1]。

#include <bits/stdc++.h>using namespace std;const int N=1010;int n,m,q;
int a[N][N],s[N][N];int main()
{scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];while(q--){int  x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);}return 0;
}

3.差分

（1）一维差分

差分与前缀和可以看成是一对逆运算。我们通过一个原数组构造出其前缀和数组，对于差分来说，也可以构造出差分数组，而差分数组正好是前缀和数组逆过来的结果：
给定一个数组a[n]，我们要构造一个新数组b[n]，使得a[i]=b[1]+b[2]+…+b[i]，可以看出a[n]成为了b[n]的前缀和数组，则我们称b[n]为a[n]的差分数组。
而构造差分数组则比较简单，用数组项的差即可。
b[0]=a[0]
b[1]=a[1]-a[0]
b[2]=a[2]-a[1]
…
b[n]=a[n]-a[n-1]
通过O(n)的时间复杂度，我们就又能从b[n]得到a[n]。
差分的用途：给定一个数组a[n]，我们现在要给数组的区间[l,r]中每一个数都加上c。如果要使用暴力循环加的话，时间复杂度就是O(n)，现在我们利用差分数组，因为a[n]是b[n]的前缀和数组，所以当b[i]改变时，也会改变a[i]以及a[i]之后的每一个数，若b[i]+c，则a[i],a[i+1],…,a[n]都会+c，所以我们可以利用这个性质，让a[l]+c，然后再让a[r]-c，这样就能达成我们的目的了。
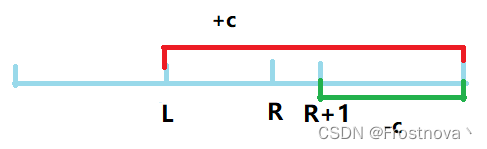
请添加图片描述
题目练习： AcWing 797. 差分

输入一个长度为n的整数序列。
接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。
请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数序列。
接下来m行，每行包含三个整数l，r，c，表示一个操作。
输出格式
共一行，包含n个整数，表示最终序列。
代码

#include <bits/stdc++.h>using namespace std;const int N=1e6+10;int n,m;
int a[N],b[N];void insert(int l,int r,int c)
{b[l]+=c;b[r+1]-=c;
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) insert(i,i,a[i]);while(m--){int l,r,c;scanf("%d%d%d",&l,&r,&c);insert(l,r,c);}for(int i=1;i<=n;i++) b[i]+=b[i-1];for(int i=1;i<=n;i++) printf("%d",b[i]);return 0;
}

（2）二维差分（差分矩阵）

如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是肯定的，这就是二维差分。
a[][]数组是b[][]数组的前缀和数组，那么b[][]是a[][]的差分数组
原数组： a[i][j]
我们来构造差分数组： b[i][j]
使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。
已知原数组a中被选中的子矩阵为以(x1,y1)为左上角，以(x2,y2)为右下角所围成的矩形区域
始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i][j]的修改，会影响到a数组中从a[i][j]及往后的每一个数。
假定我们已经构造好了b数组，类比一维差分，我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c
b[x1][y1]+=c;
b[x1,][y2+1]-=c;
b[x2+1][y1]-=c;
b[x2+1][y2+1]+=c;

#include <bits/stdc++.h>using namespace std;const int N=1010;int n,m,q;
int a[N][N],b[N][N];void insert(int x1,int y1,int x2,int y2,int c)
{b[x1][y1]+=c;b[x2+1][y1]-=c;b[x1][y2+1]-=c;b[x2+1][y2+1]+=c;
}int main()
{scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)insert(i,j,i,j,a[i][j]);while(q--){int x1,x2,y1,y2,c;scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);insert(x1,y1,x2,y2,c);}for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)printf("%d ",b[i][j]);puts(""); }           return 0;
}