- 解决高偏差和高方差的新方法
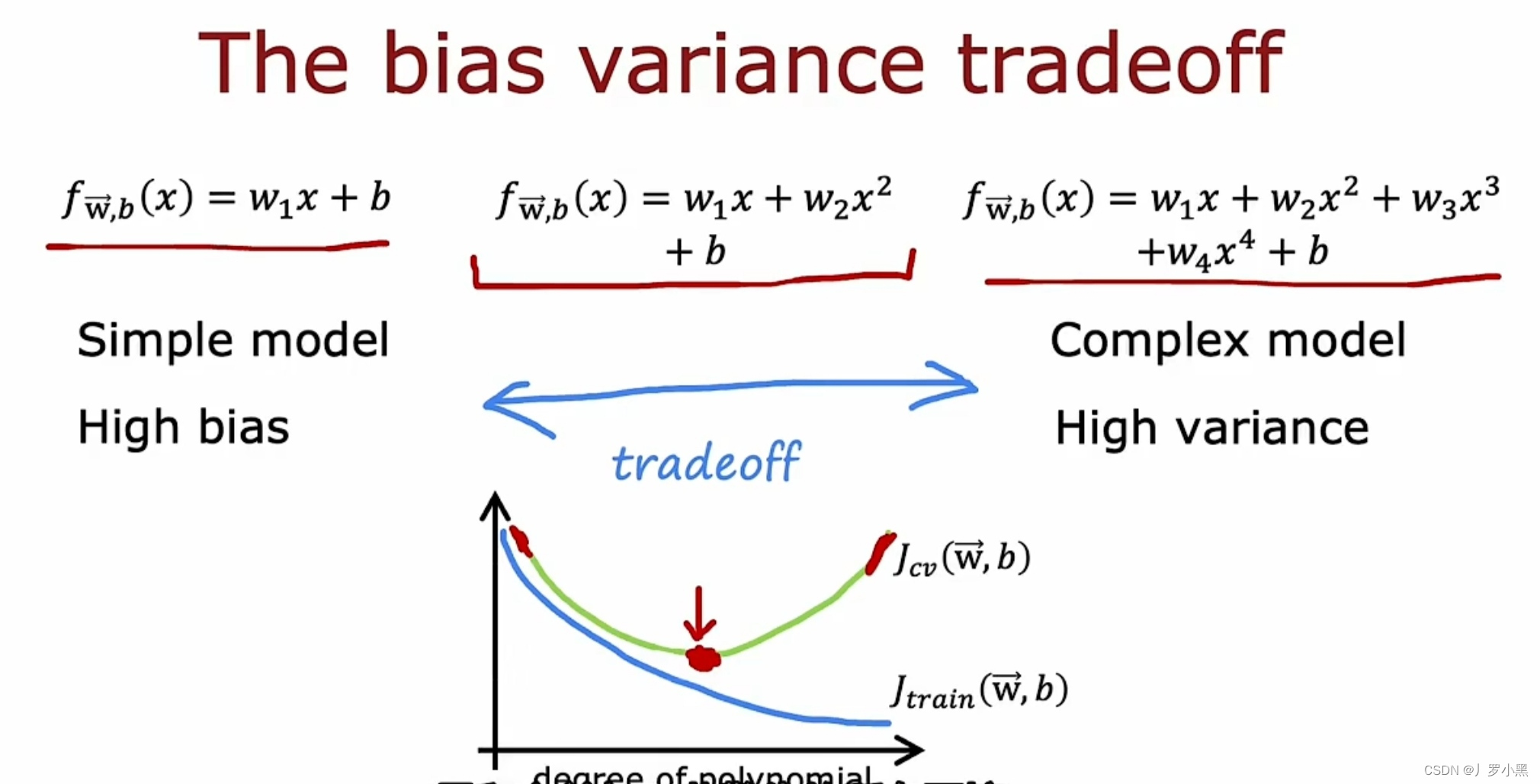
- 之前,我们需要通过选取多项式次数以及正则化参数λ,来平衡高方差和高偏差
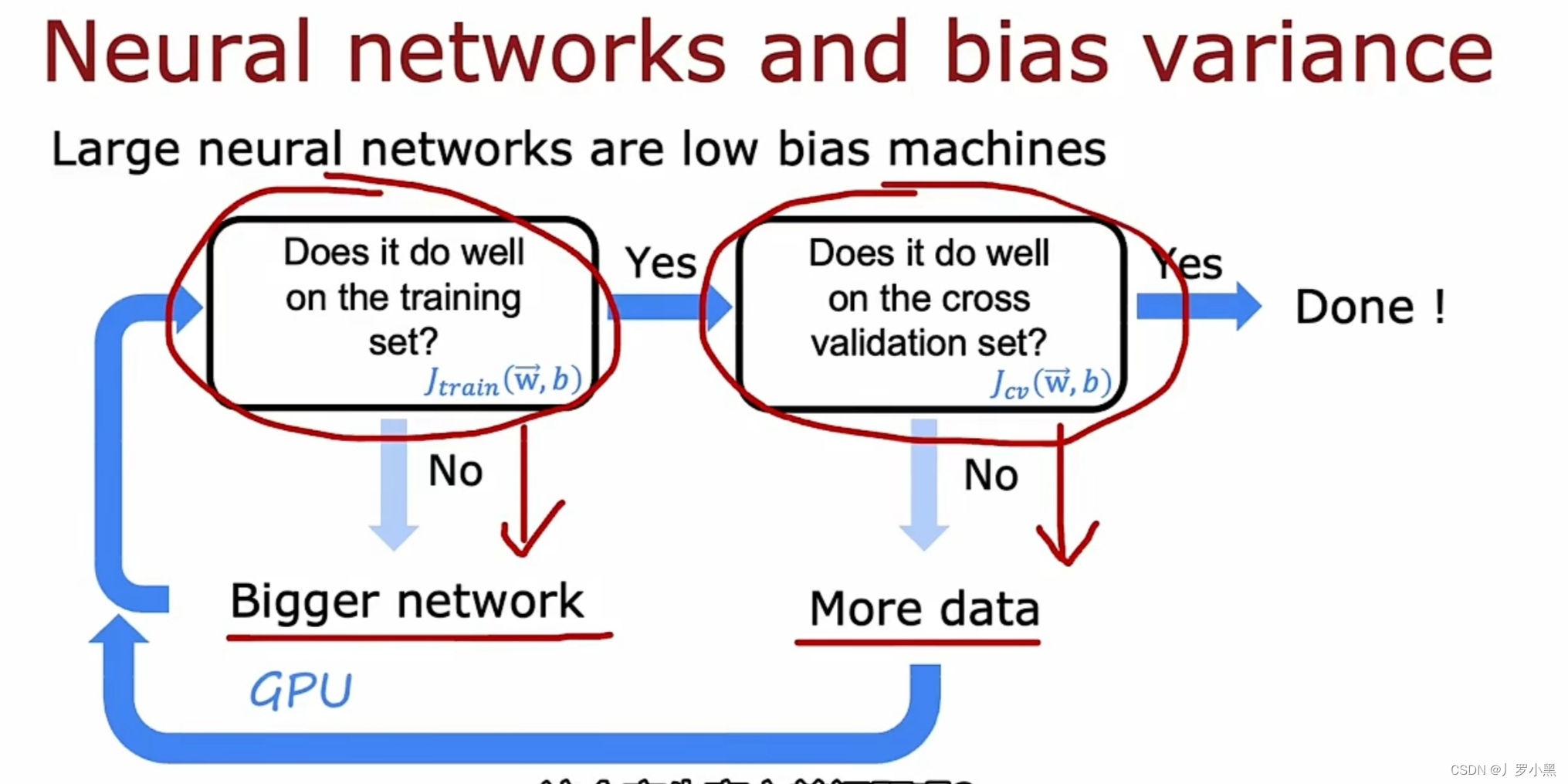
- 只要训练集不是特别大,那么一个大型的神经网络总能很好的适应训练集,即它的Jtrain很低
- 由此可以得出,若要减小Jtrain,可以增大神经网络,即增加隐藏层的层数或增加单层隐藏层中的神经元
- 而若要降低Jcv,可以增大训练集。最终,只有Jtrain和Jcv均很小,此模型才算解决了高方差和高偏差
- 此方法的局限性:首先,更大的神经网络,意味着更昂贵的计算成本。其次,有时训练数据只有这么多,无法增加
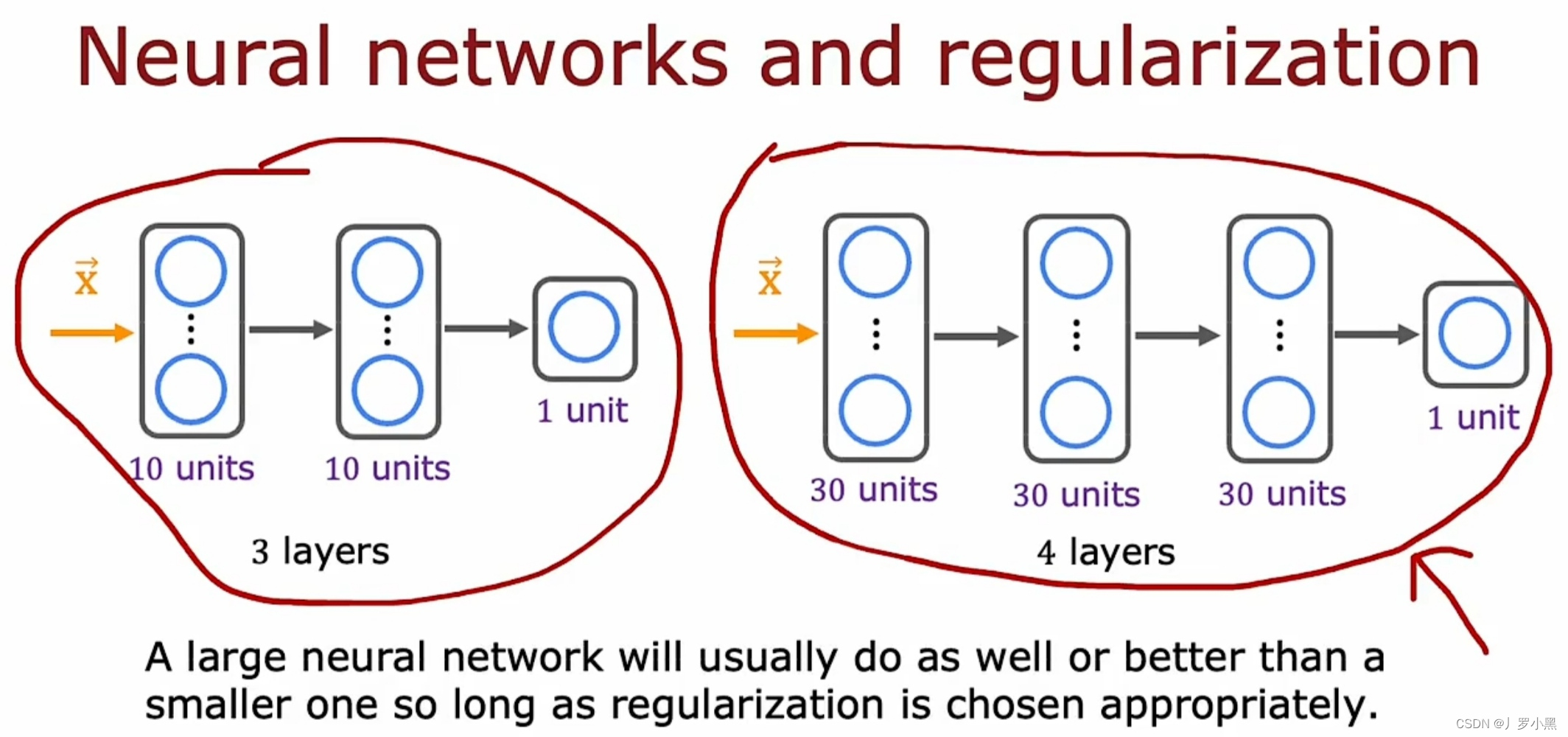
- 一个大型的神经网络如果进行适当的正则化后,不会增大Jcv
- 因此只要正则化得当,大型的神经网络不会有过拟合的风险,且它通常比小型的神经网络要好或一样好,但是它会增加计算成本以及增加计算的时间

- 通常我们不会对参数b进行正则化,因为无论是否正则化b都对结果没什么影响
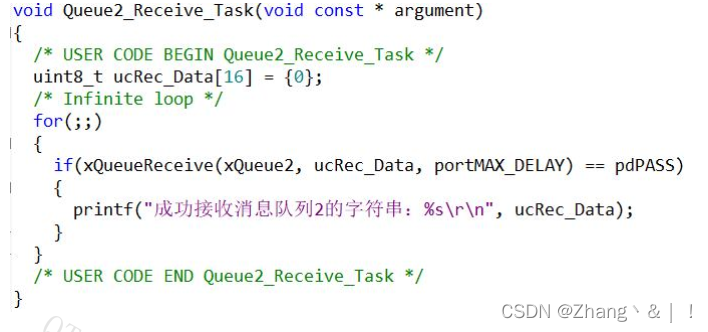
- 上图为,在tensorflow中实现正则化的代码与不实现正则化的代码进行了对比