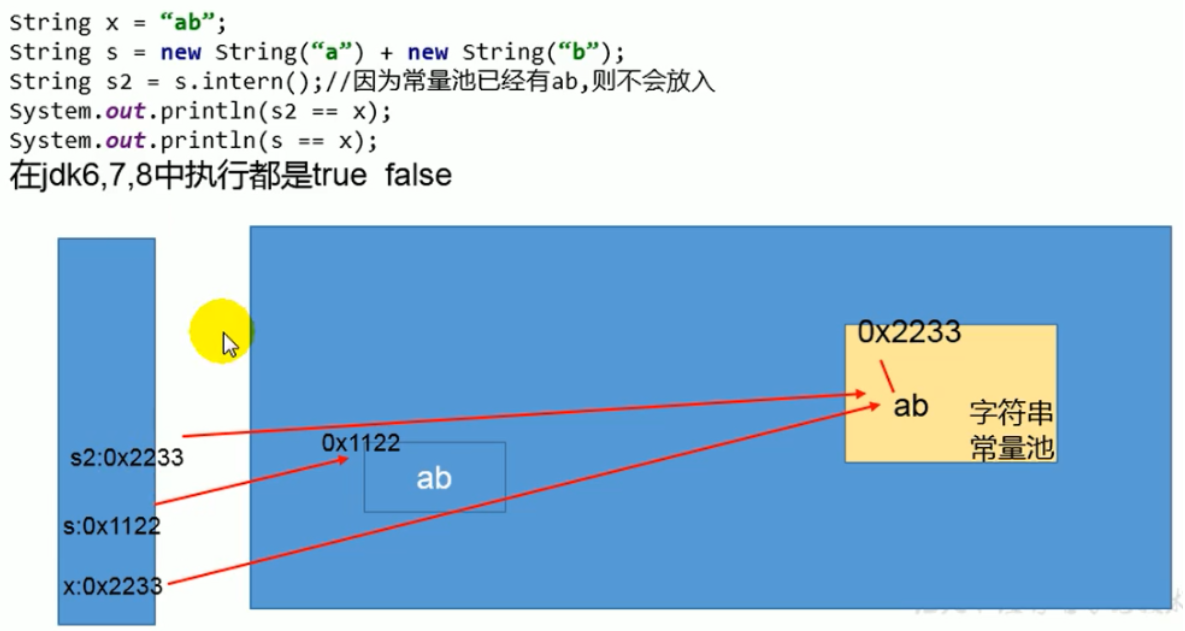
word2vec使用语言天生具备序列这一特性训练得到词语的向量表示。而在图结构上,则存在无法序列的难题,因为图结构它不具备序列特性,就无法得到图节点的表示。deepwalk 的作者提出:可以使用在图上随机游走的方式得到一串序列,然后再根据得到游走序列进行node2vec的训练,进而获取得到图节点的表示。本质上deepwalk和word2vec师出同门(来自同一个思想),deepwalk算法的提出为图结构学习打开了新的天地。
1. 前言
目前主流算法可大致分为两类:walk-based 的图嵌入算法(GE,Graph Emebdding )和 message-passing-based 的图神经网络算法(GNN)。
- GE类算法主要包括有
deepwalk、metapath2vec; - 基于消息传递机制的图神经网络算法的经典论文则是GCN,GAT等。
因为内容过多,本期讲解分两期,第一期首先介绍GE类算法,第二期介绍图神经网络算法。GE类的算法经典的还属deepwalk,所以本期首先围绕deepwalk这篇论文进行介绍。
接触过word2vec 的同学都知道,word2vec的思想一改往日的one-hot囧境,将每个word映射成一个高维向量,这些学习到的的vector便具备了一定的特性,可以直接在下游任务中使用。有关word2vec这里不再叙述,更详细内容可以参考我之前的文章。
但是如果想得到图结构中顶点表示该怎么办呢?毕竟图结构与语言序列不同,图上的一个顶点可能有很多个连接点,而文本序列则是单线条,如下图所示,可以看出图结构与文本序列有着非常大的差异。
那就没有办法去解决图节点的表示学习了吗?
当然不是!而且方法还有很多,聪明的前辈们提出了一种叫做『deepwalk』的算法,这个算法着实让我惊艳。本质上说,deepwalk算法是基于图上的word2vec,而启发作者的其实是:由于二者数据分布(自然语言的词频和随机游走得到子图的节点的频率)存在一定的相似性。

所以说,很多精妙的想法不是凭空造出来的,背后其实是有数据统计支撑的。
2. 思想
文本序列虽然只是一个序列,但是我们可以想象有一张巨大的由各个单词组成的图,我们随机从图上连接几个顶点就组成了一句话。例如『论文解析之deepwalk』其实就是从一张偌大的图中挑选出这么几个单词组成的一句话,如下图所示:
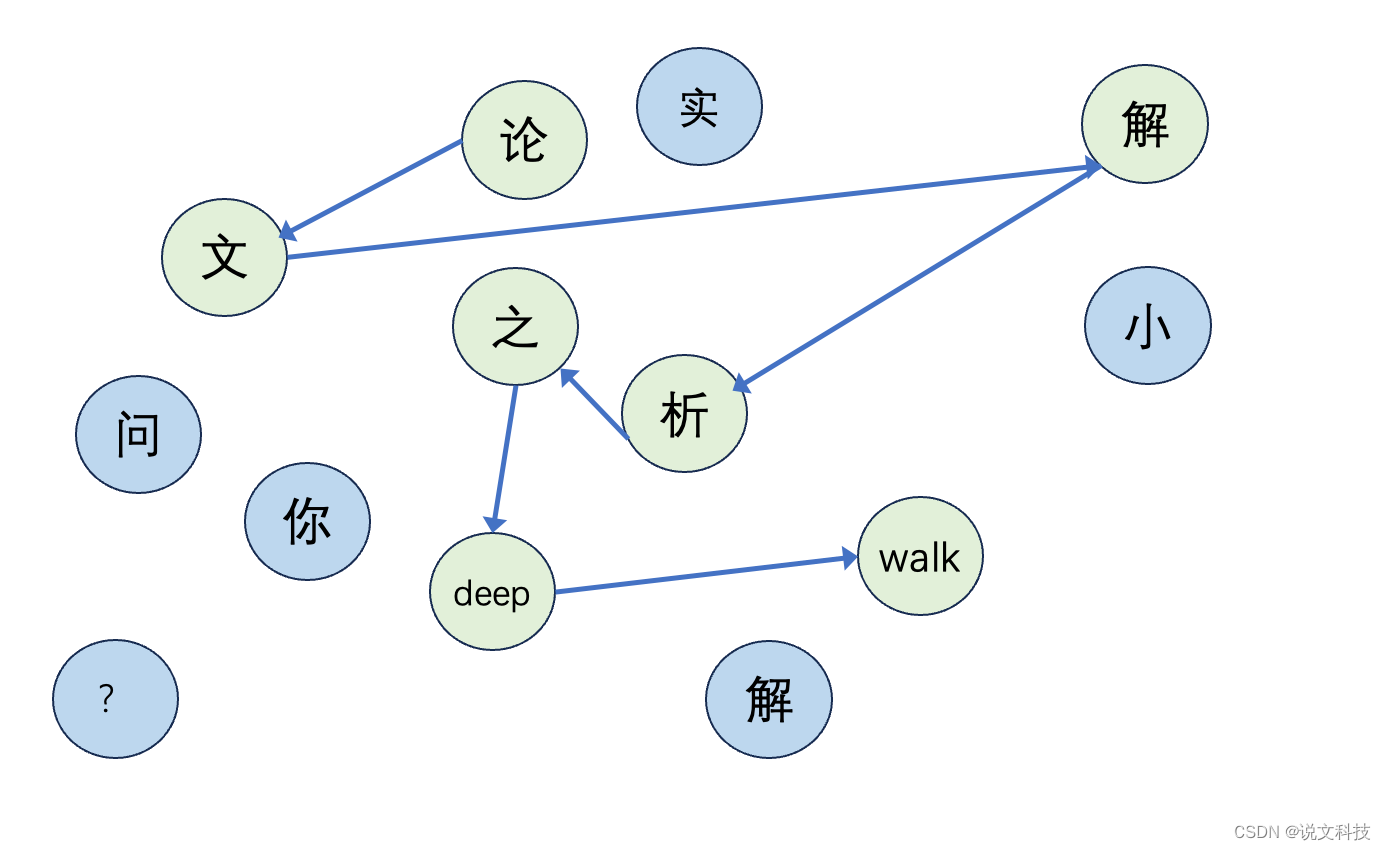
那么对于其它的图,我们也可以这么做。即:从一张大图上随机游走,这样便得到了一串序列。将这得到的序列便可以利用word2vec的方法来学习节点的表示了。
想法是不是很精妙?真的很精妙!其实我们自己在解决问题的时候,也需要抱着这样的『转换』思想,如果直接求A不成,那么能否利用已有的知识求A?这再次说明问题的转化能力是一个非常重要的能力。
既然问题已经得到了转化,接下来的工作就比较简单了,可以直接利用word2vec中的算法(如Skip gram算法)去训练得到图节点的embedding。
3. 模型
3.1 模型构造
deepwalk 算法主要包含两部分:第一部分是random walk generator;第二部分是一个更新程序。

- 采样方法
deepwalk中的采样方法其实是非常简单的均匀采样。下文中介绍到了这一采样算法:

step1. 首先随机采样一个节点作为此次walk的根节点。
step2. 接着从采样序列的最后一个节点的邻居中再随机选一个节点
step3. 直到采样序列的最大长度达成。
本文采取的实验参数是:将每个节点都做一次根节点,随机游走可以达到最长的长度为t。 对应的算法伪代码如下所示:

- 更新程序
在得到随机游走的序列后,便可以使用word2vec算法获取节点的embedding了。deepwalk算法使用的是SkipGram算法。SkipGram算法的思想很简单,就是利用当前词去预测周围词。具体来看Skip-Gram 的算法伪代码。

p ( u k ∣ ϕ ( v j ) p(u_k | \phi(v_j) p(uk∣ϕ(vj) 其实就是求在 v j v_j vj 这个顶点出现的条件下,顶点 u k u_k uk出现的概率,思想就是这么简单。那么损失函数也很好定义,直接取log后再取负数即可。但这里有个小trick点,(其实这个点也是训练word2vec 中的一个关键点),就是计算 p ( u k ∣ ϕ ( v j ) ) p(u_k|\phi(v_j)) p(uk∣ϕ(vj))时,我们一般都是用softmax来计算这个概率,softmax的计算公式是
p ( x j ) = e x p ( x j ) ∑ i n e x p ( x i ) p(x_j) = \frac{exp(x_j)}{\sum_i^n{exp(x_i)}} p(xj)=∑inexp(xi)exp(xj)
但是词表的大小一般都是上万起步,如果要逐项计算 e x p ( x i ) exp(x_i) exp(xi),则非常浪费计算资源,那么有没有可以解决这个问题的方法呢?聪明的前辈们已经替我们想到了解决方法,那就是使用:负采样或者Hierarchical softmax方法。本文的作者使用的是HIerarchical softmax。因为skip gram算法在之前的文章中已经分析过,这里直接跳过。接下来我就再花费大家的一点时间来给大家介绍一下这个Hierarchical softmax。
3.2 Skip Gram
有兴趣的请翻前文。
3.3 Hierarchical softmax
这个Hierarchical softmax的算法思想其实非常简单,一言以蔽之:能否减少分类节点的个数(其实本质上也是负采样,只不过利用了完全二叉树去实现这个负采样的过程)。
例如:假设一部词典一共有8个单词,那么就可以构建一个如下所示的二叉树。
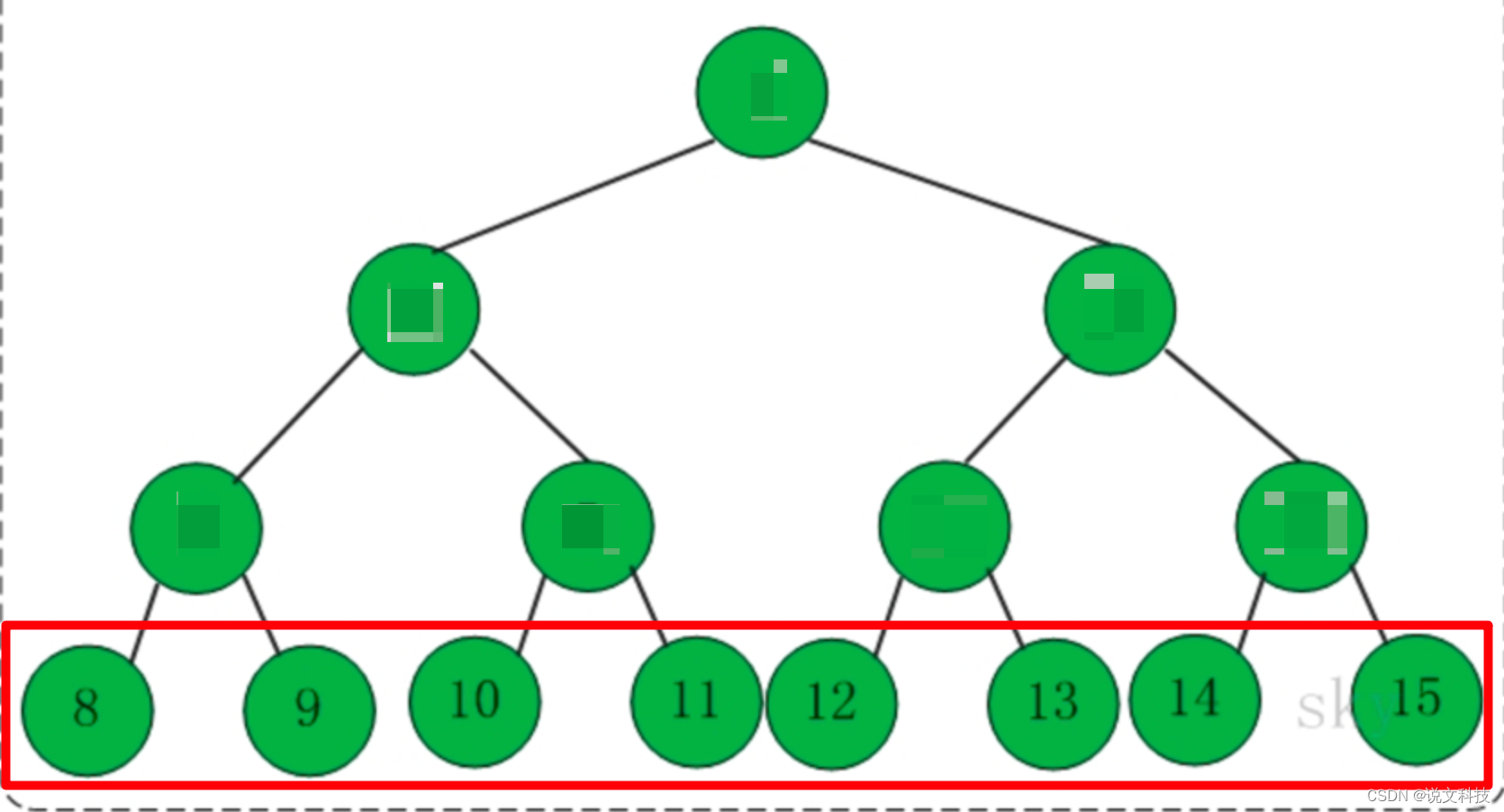
其中:
- 叶子节点与每个单词对应。
那么求上下文单词 u k u_k uk在条件 v j v_j vj出现时的概率这一问题就转化成了到达这个叶子节点的概率问题。 而到达每个叶子节点的概率是唯一的(因为路径各不相同)。那么之前的这个式子 p ( u k ∣ ϕ ( v j ) p(u_k | \phi(v_j) p(uk∣ϕ(vj) 就可以转化成由下面这个式子去求解:
∏ i m ( p ( y i ∣ v j ) ) \prod_i^m(p(y_i|v_j)) i∏m(p(yi∣vj))
其中, y i y_i yi的取值范围为{0,1},这里的m其实就是这棵二叉树的深度,也就是 l o g V log V logV向上取整。比如这里就是 l o g 8 = 3 log8=3 log8=3。
这么一套操作下来之后,就可以把原本一个线性的复杂度时间O(v)降到了O(logV),厉害吧!原文给出了一个比较直观的例子,用于理解Hierarchical softmax,如下:
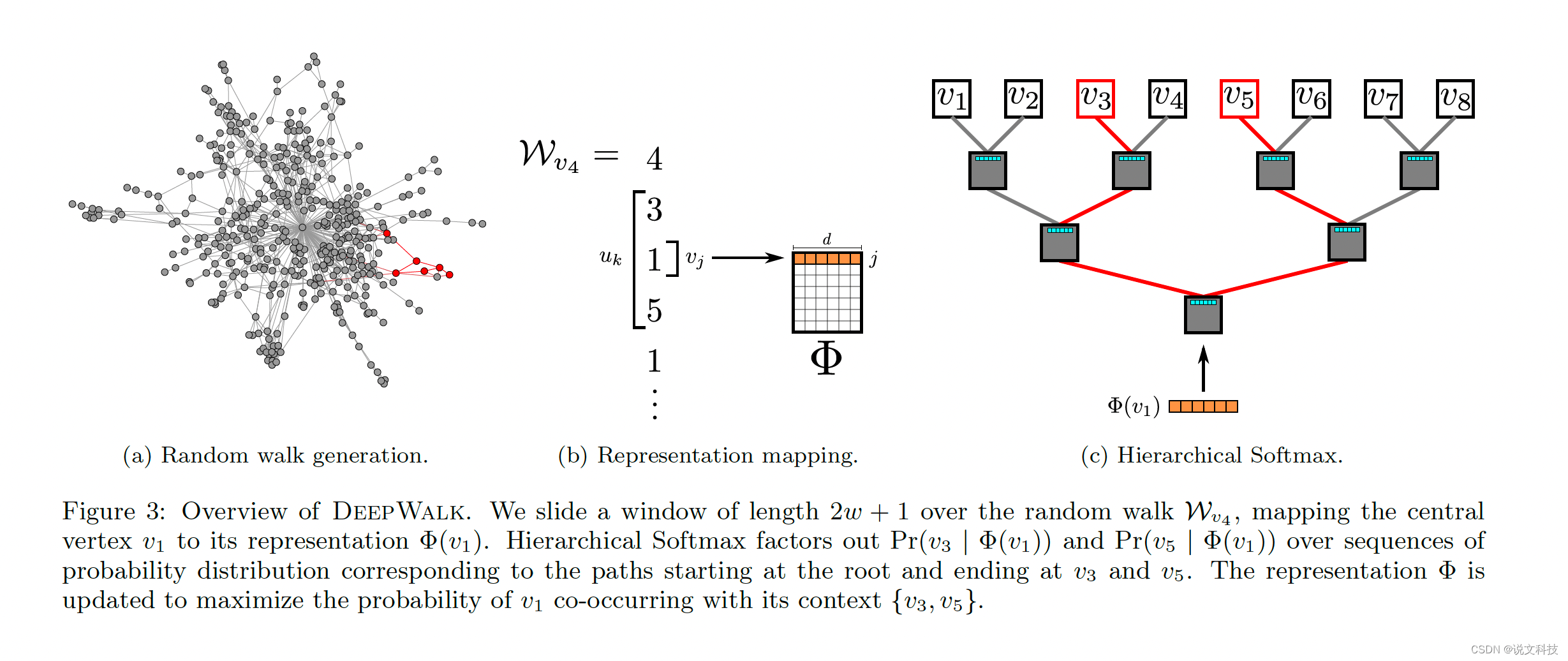
在求得这个概率之后,就可以转头去做优化了。
优化算法
deepwalk 论文的作者采取的是 SGD(stochastic gradient descent )优化损失。这里没有什么好介绍的,直接跳过了。到此为止,整个算法的核心内容已经介绍完毕了。接下来看看这个算法的实际效果如何?
3. 实际效果
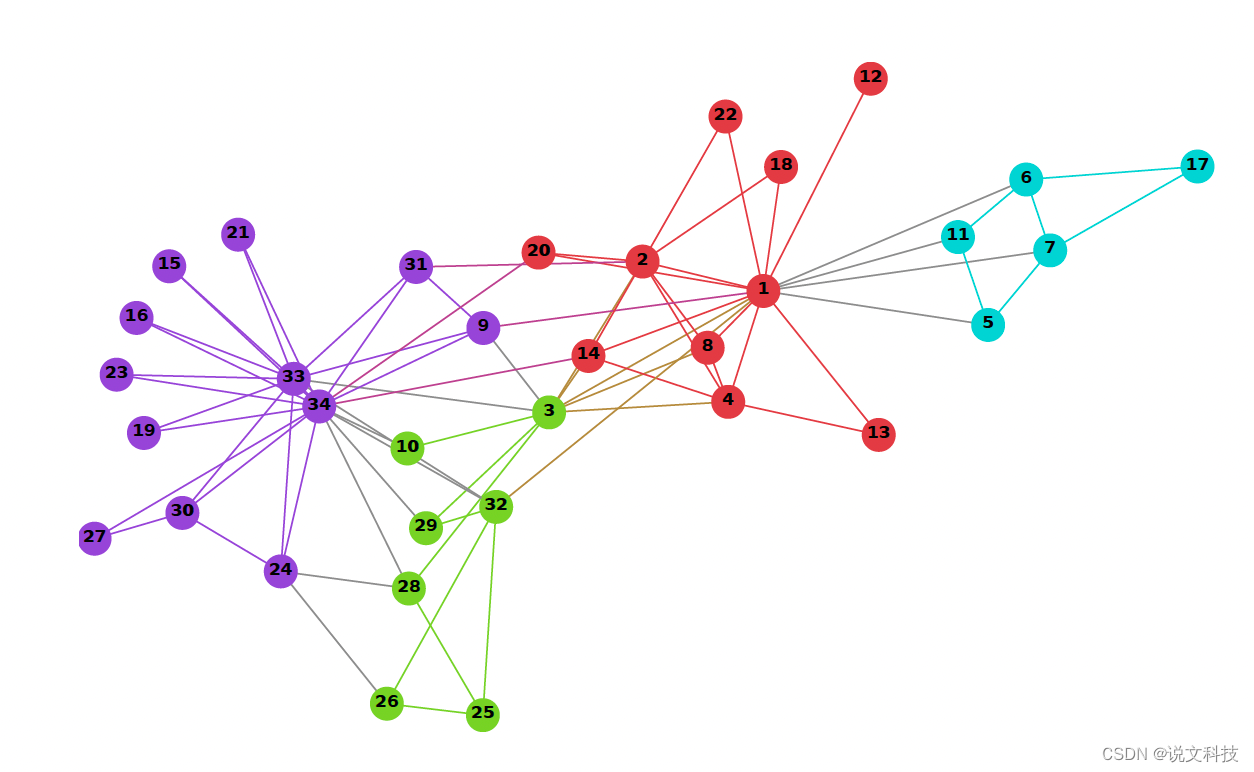
deepwalk论文作者给出了一个效果示例图,如下图所示:
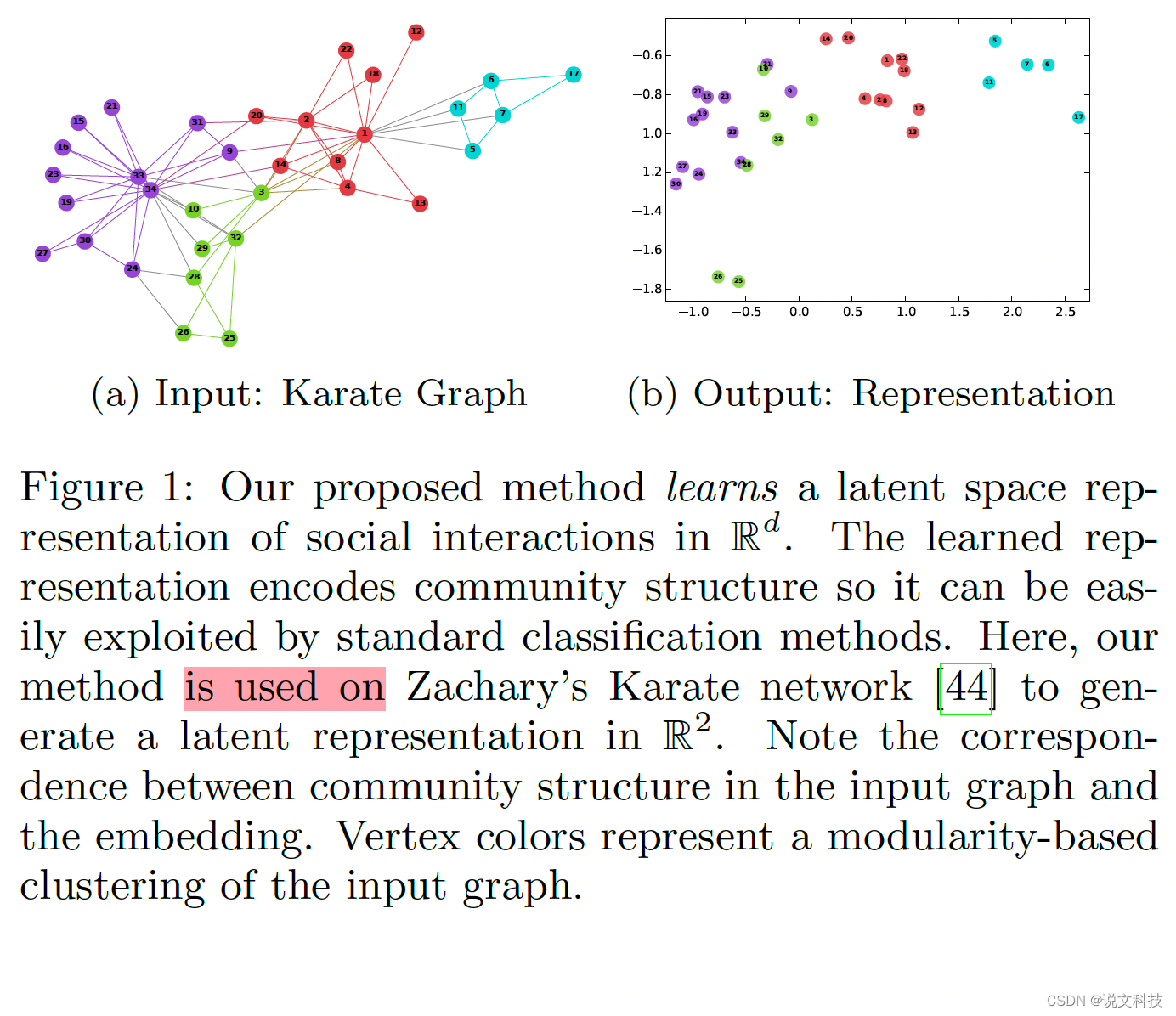
左侧是一个图结构信息,右侧是根据学习到的embedding得到的一个二维展示,可以看出图结构和节点表示几乎能够一一对应起来(顶点的颜色表示输入图对一个基于模块的聚类)。
4. 发现
文章中提出了许多非常有意思的知识。坦白讲,在没有仔细看这篇文章之前,有一些知识点我是不了解的,比如「zipf's laws」。
4.1 zipf’s law
zipfs'law,又称齐夫定律,这是一个经验定律。该定律表示:一个单词的排名 r r r和这个单词的出现频率 p p p成反比,也即 r ∗ p = k r*p = k r∗p=k。用图像表示则是如下这个样子:
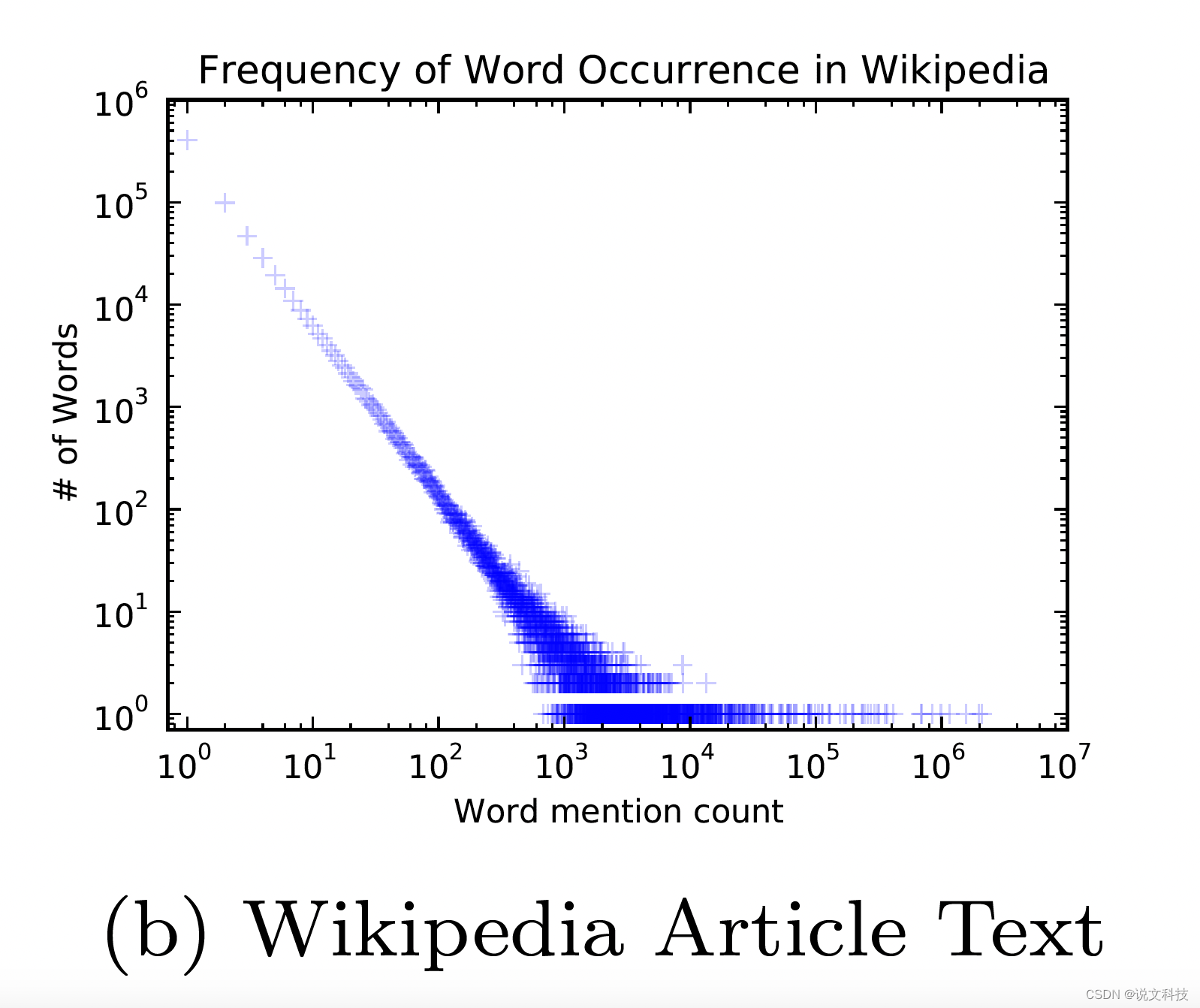
y=1/x 这个函数的图像长这样:
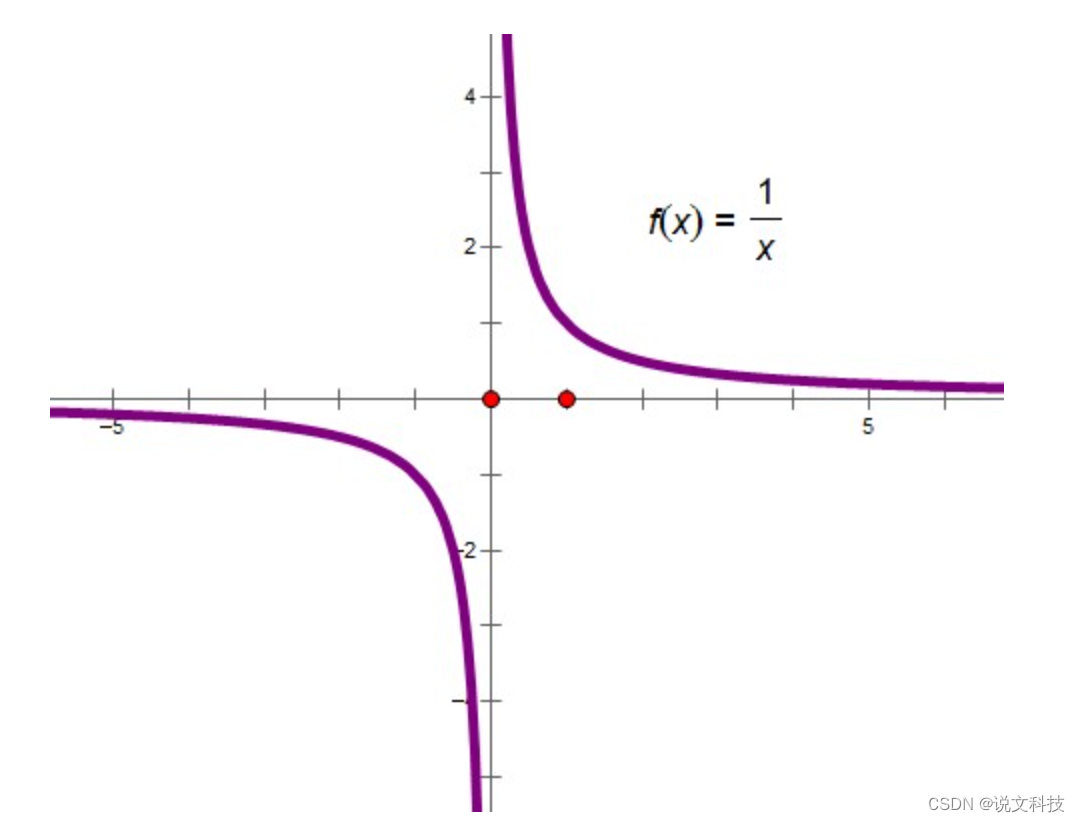
(齐夫定律的图像要稍微直一些)。作者发现,如果原始图的顶点服从齐夫定律,那么根据随机游走选出来的子图的频次也会满足齐夫定律。

这个时候作者就想到,如果满足齐夫定律的自然语言可以用语言模型建模,那么用随机游走方式得到的子图是否也可以通过语言模型来建模呢?于是接着有了后面使用SkipGram算法训练embedding,才有了这篇论文的诞生。
5. 实验效果
最后,作者给出了deepwalk算法在三个数据集上的多标签分类实验效果,如下所示。总结成一个词:惊艳!
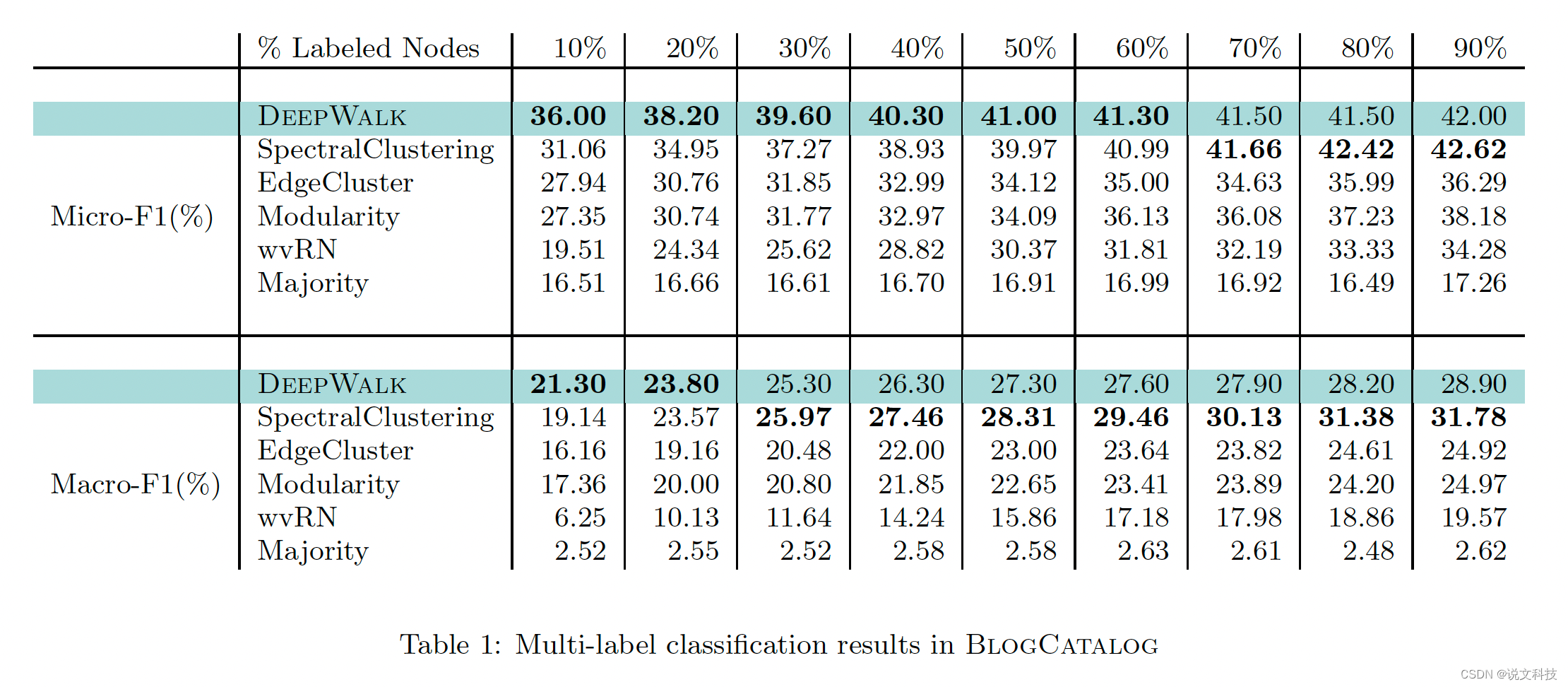
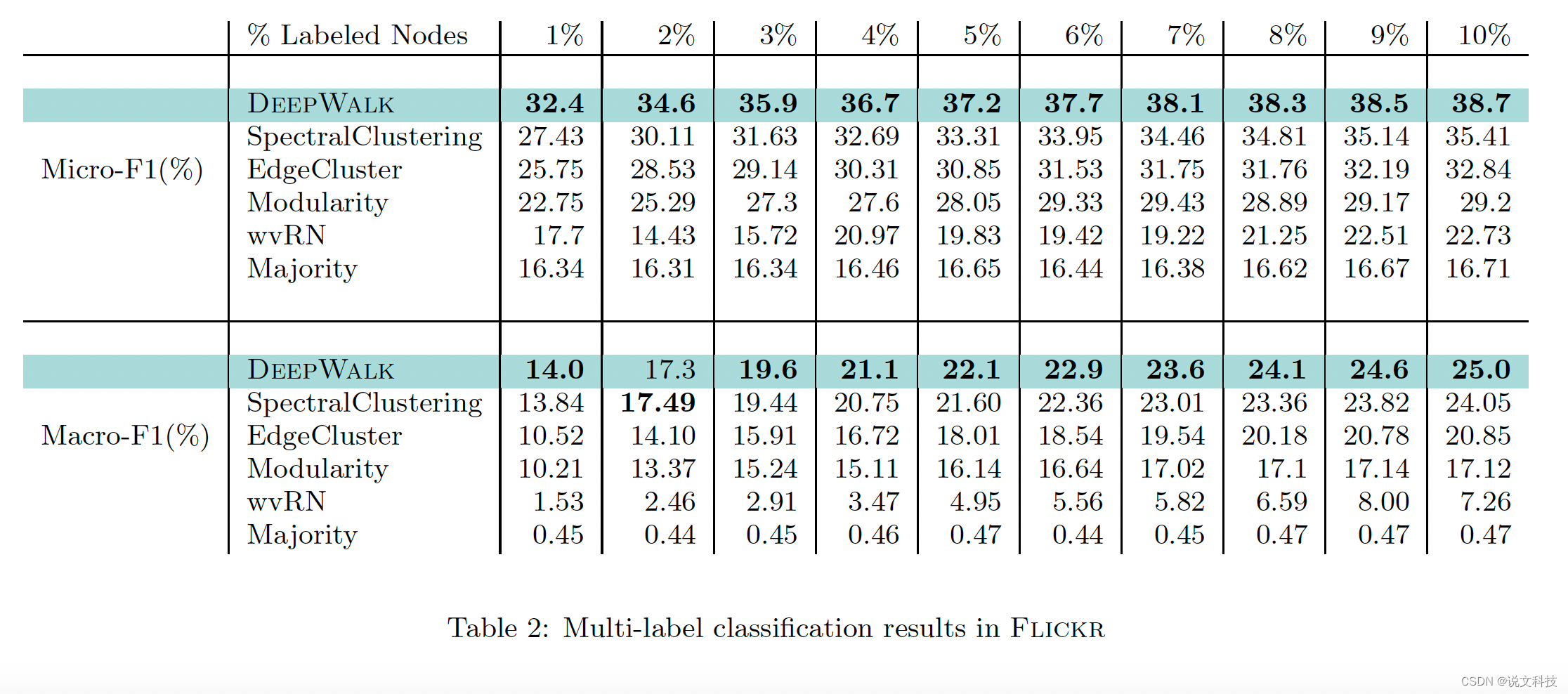
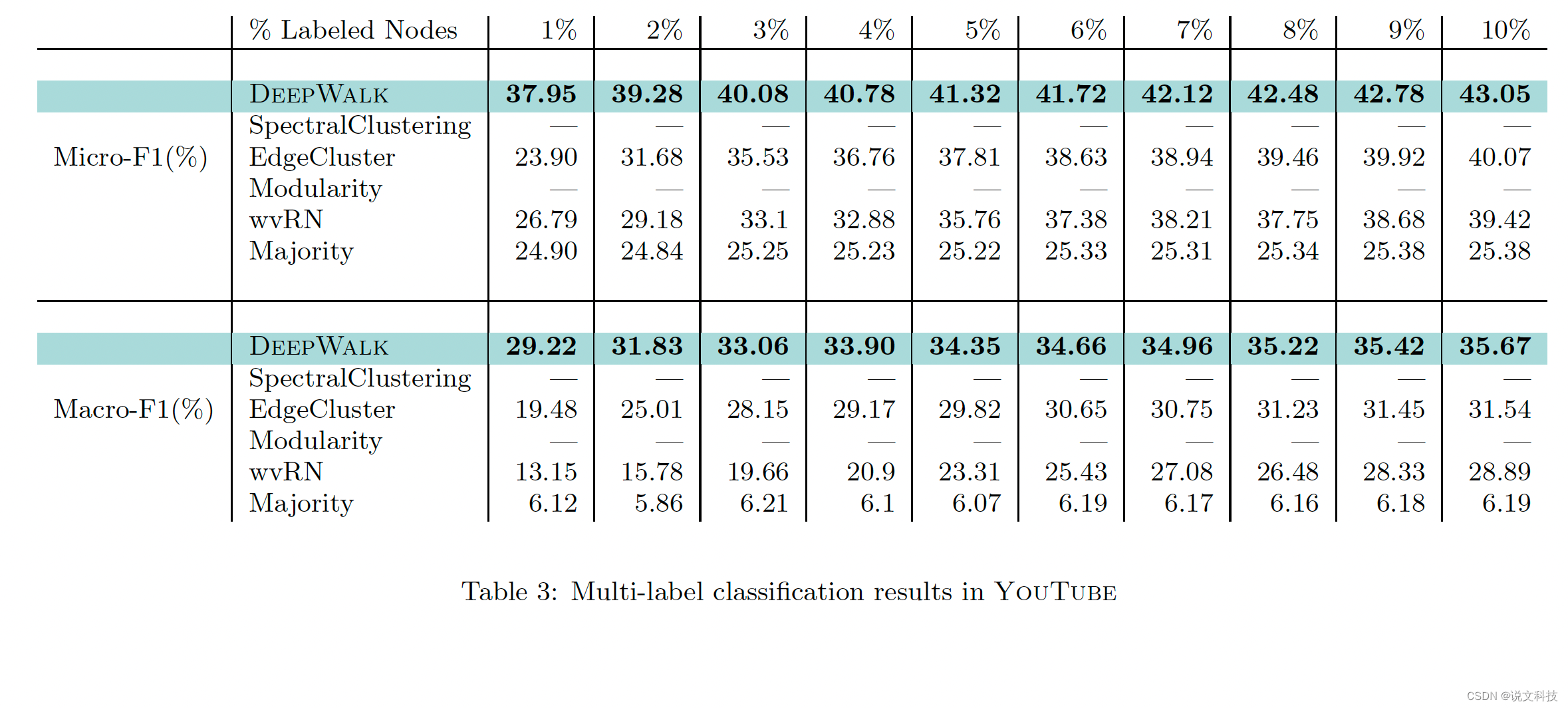
好了,到此第二期的经典论文阅读的第一部分工作已经结束,后面再围绕metapath2vec进行介绍。高质量分享实属不易,期待各位同学们的评论和赞赏哟。