没参加这次蓝桥杯算法赛,十四届蓝桥杯被狂虐,对算法又爱又恨,爱我会做的题,痛恨我连题都读不懂的题😭,十四届填空只做对一个,今天闲的蛋疼想看看这次比赛能做对几个。
暂时没找到题目,这是网上找的简略版,看了看就知道蓝桥杯前几道题就喜欢考数学思维和十四届一样
试题 A: 报数游戏
(简洁版)从小到大排列是20或24倍数的正整数,前10个数依次是:”20 24 40 48 60 72 80 96 100 120“,求第202420242024个数是多少?(填空题)
解题思路:
最开始想的是求求它俩的最小公倍数是120发现没啥用,然后再发现24比20多4,也就是24向前叠加5次就整整多出来一个20,然后再在纸上画画发现了每10次一循环:
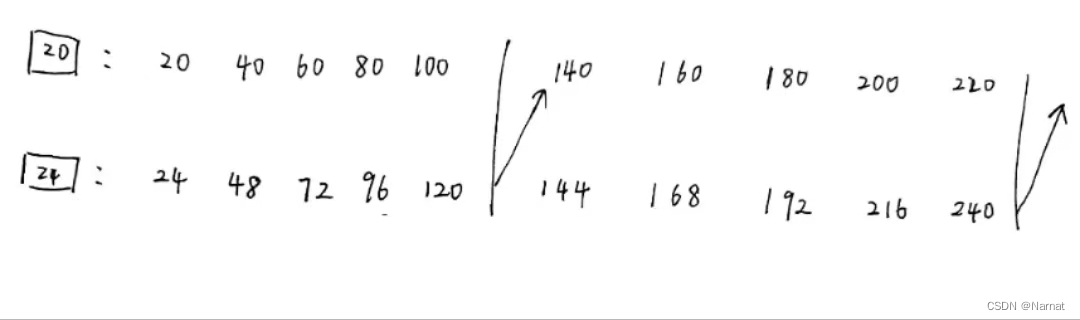
可以看出第10个数是24 * 5,第20个数是24 * 10,那么202420242024可以分成202420242020 + 4,最后发现偶数4也是24结尾,那么答案就是202420242024 / 2 * 24

试题 B: 类斐波那契循环数
(个人理解:)将一个n位的数字按一定的规则排成一个数列。
规则:
这个数列的起始部分分别为该数字每一位上的数。例如:数字(12345)排成数列是【1,2,3,4,5】。
这个数列的其它部分分别为从当前数列的最后一位起,前n项的和。例如数字(12345,共5位)排成数列【1,2,3,4,5,(?),…】,此时数列的第6个数就是从当前数列的最后一位起前5项的和,即(1+2+3+4+5=15)【1,2,3,4,5,15】;第7个数就是从当前数列的最后一位起前5项的和,即(2+3+4+5+15=29)【1,2,3,4,5,15,29】;…
如果这个数列中包含这个数字本身,那么这个数就是类斐波那契循环数。
求从0~10^7范围中最大的类斐波那契循环数。(填空题)
解题思路:
仔细做了做例子发现:
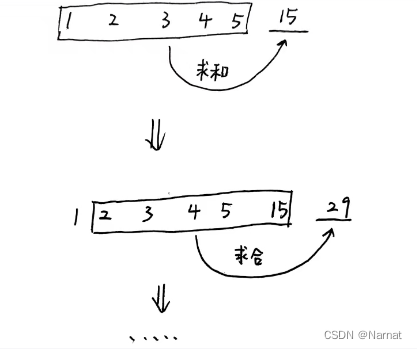
发现有点像滑动窗口,求新数后窗口移动一下,所以想着将整个过程放在一个数组里,但是这样一整每次数组的长度都是不定的,不好定义数组的长度,且求到新数后,数组前面的区域就没用了,所以就想着能否用一个定长数组来做滑动窗口,且所有区域都用的上
分析一下上面例子求出新数15后第一个数1就对求下一个数29来说没用了,为什么不把15放在1的位置,以此类推29放在2的位置
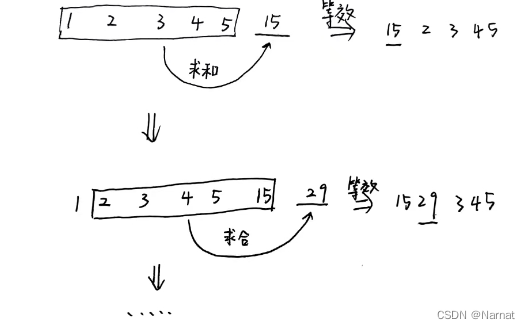
这样就好整了,数组大小就等于数字的位数,还需要一个K指针在整个数组中循环移动用%Length就解决了
说实话这个灵感来源于我嵌入式对页面切换的处理…
最后看是怎么停止了,题目说了这个数列中包含这个数本身那么这个数就是类斐波那契循环数,因为每次求得得新数都是递增的,所以如果新数都大于原始数的话,那么说明这个数不是类斐波那契循环数
既然求类斐波那契循环数的整个逻辑模式都搞明白了,剩下就是用代码实现上述的功能需求了:
import java.util.*;public class Main {static int END = 10000000;public static void main(String[] args) {int MaxNumber = 0;for(int i = 1; i <= END; i ++) { // 由1开始int Length = GetNumnberLength(i);int Array[] = new int[Length];NumbertoArray(Array, i);int k = 0;while(true) {Array[k] = ListNumberSum(Array);if(Array[k] == i || Array[k] > i) break; // 要么是类斐波那契循环数要么不是k = (k + 1) % Length;}if(Array[k] == i) { // 是的话更新MaxNumberif(MaxNumber <= i) {MaxNumber = i;}}}System.out.println(MaxNumber);}public static int GetNumnberLength(int number) {int len = 0;while(number > 0) {len ++;number = number / 10;}return len;}public static void NumbertoArray(int array[], int number) {for(int i = array.length - 1; i >= 0; i --) {array[i] = number % 10;number = number / 10;}}public static int ListNumberSum(int array[]) {int sum = 0;for(int i = 0; i < array.length; i ++) sum = sum + array[i];return sum;}
}其中while循环应该也循环不了几百次,整个时间复杂度应该等于10^7 * while循环次数,超过不了10^9复杂度,计算机一两秒就算出来了。
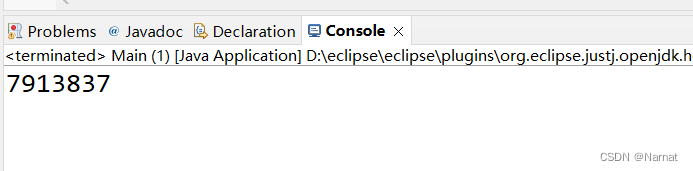
答案: