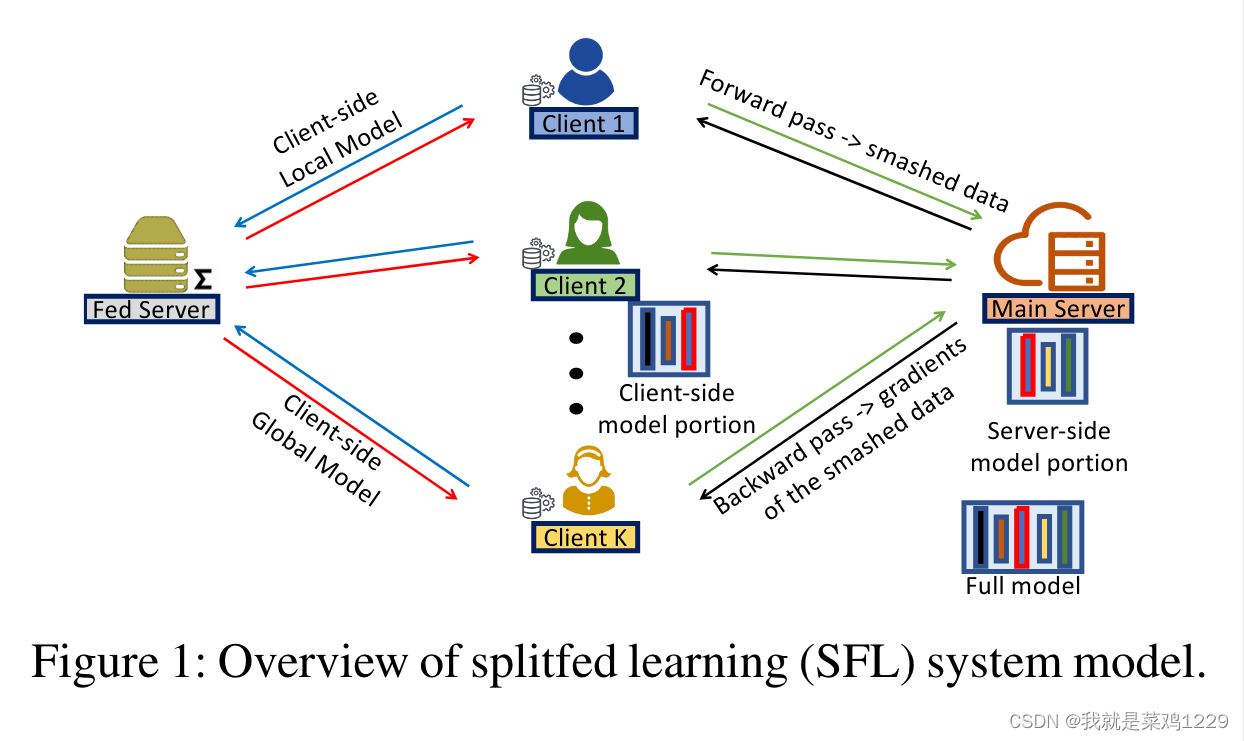
Eigen的头文件定义了多种类型,但是对于简单的来说,使用MatrixXd就足够了,MatrixXd表示任意尺寸的矩阵,但是要注意数据类型是double的。Eigen/Dense的头文件定义了所有MatrixXd和相关类型的成员函数。所有头文件中定义的函数都是在Eigen这个命名空间下的。
我们再次分析一下上面的代码:
MatrixXd m(2,2); // 定义两行两列,前面是行数,后面是列数m(0,0) = 3; // (0, 0) 位置是3m(1,0) = 2.5; // (1, 0) 位置是2.5m(0,1) = -1;m(1,1) = m(1,0) + m(0,1); // m(1,0) 返回的是double值,直接运算
再来一个例子,将矩阵和向量结合起来:
int main()
{MatrixXd m = MatrixXd::Random(3,3);std::cout << "m_before =" << std::endl << m << std::endl;m = (m + MatrixXd::Constant(3,3,1.2)) * 50;std::cout << "m =" << std::endl << m << std::endl;VectorXd v(3);v << 1, 2, 3;std::cout << "v =" << std::endl << v << std::endl;std::cout << "m * v =" << std::endl << m * v << std::endl;
}
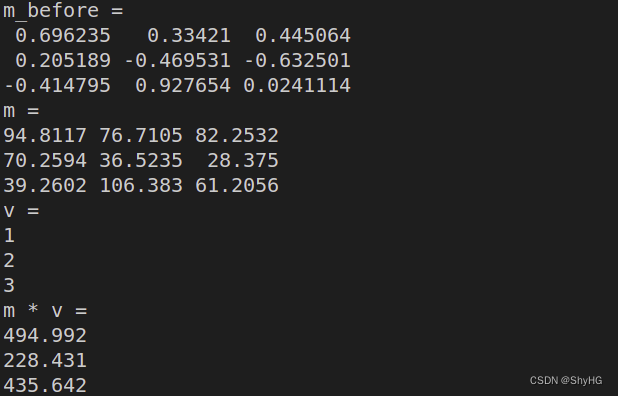
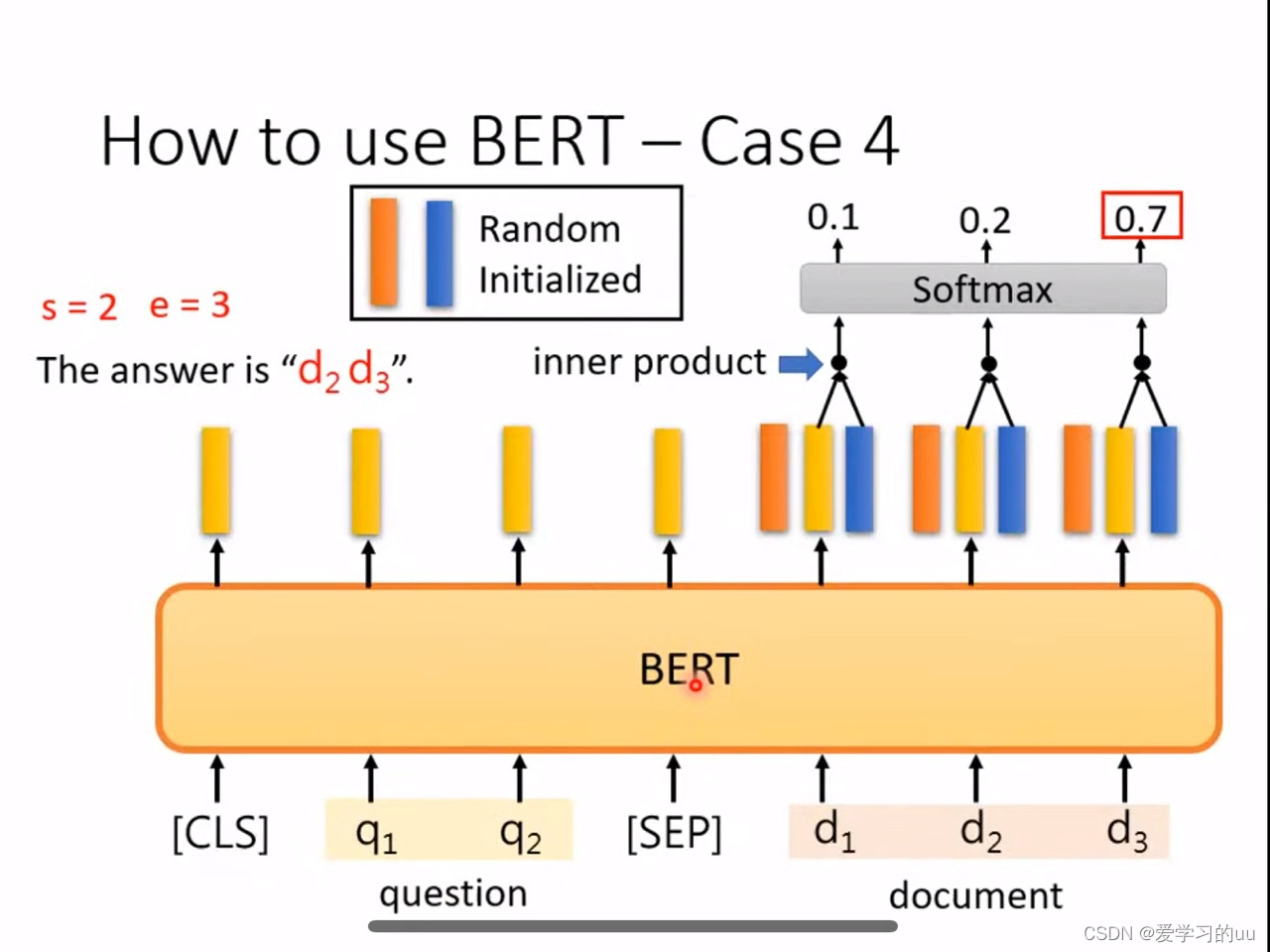
我们一起分析一下,首先调用了一个 MatrixXd::Random(3,3)来生成一个(3, 3)的随机数矩阵,对于这个函数有Numbers are uniformly spread through their whole definition range for integer types, and in the [-1:1] range for floating point scalar types.这样的解释,是说是返回一个在[-1:1]的均匀分布,同np.random.rand(3, 3),但是numpy返回的是[0, 1)范围。然后使用MatrixXd::Constant(3,3,1.2)生成一个3*3每个值都是1.2的矩阵,相当于numpy里面的fill()函数咯?
还有就是利用VectorXd v(3);来生成一个d维的列向量(注意,是列方向的,也就是[1, d]),并且使用<<来设置值,最后使用*来完成矩阵和向量的乘法,一个[3, 3]矩阵和一个[3, 1]的矩阵相乘,得到一个[3, 1]的结果。
当然,对于向量的初始化,也可以使用Matrix3d m = Matrix3d::Random(); Vector3d v(1,2,3);这样来初始化,但是对于有固定形状的变量,没有必要,等到我们后面学到动态形状你就能深深体会了。但是使用固定大小的矩阵和向量有两个优点。编译器发出更好(更快)的代码,因为它知道矩阵和向量的大小。在类型中指定大小还允许在编译时进行更严格的检查。例如,如果你尝试将Matrix4d (4 × 4矩阵)与Vector3d(大小为3的向量)相乘,编译器将会报错。然而,使用多类型会增加编译时间和可执行文件的大小。在编译时也可能不知道矩阵的大小。经验法则是对于4 × 4或更小的大小使用固定大小的矩阵(这段是直接机翻的)。