一、配电网重构原理

配电网重构是指在满足配电网运行基本约束的前提下，通过改变配电网中一个或多个开关的状态对配电网中一个或多个指标进行优化。通过配电网重构，可以在不增加设备投资的情况下，充分发挥配电系统的潜力，提高系统的性能指标，具有较好的经济效益。

配电网重构后的系统应保持径向拓扑，不出现环路或者孤岛，如果随机生成配网的结构，会有大量无效状态，因此在生成初始粒子和粒子迭代时可以利用一定的算法保证状态的有效性。

为了避免出现环网结构，先假设配网中所有开关都闭合，会形成一些回路，每个回路有且仅有一个开关断开；为了避免出现孤岛，在环路的公共支路中最多只有一个开关断开，在有条回路汇集的节点周围最多只有个开关断开，这样便保证了配电网重构后的系统保持径向拓扑。

同时配网重构是一个0-1规划问题，决策变量为各个开关的开断情况，一般的粒子群算法是针对连续变量，要用到配电网重构中，需要稍做修改。

原本位置更新公式和配电网重构的决策变量不匹配，为了将粒子位置映射到{0,1}中，还要引入sigmoid函数：

 

按照这样的方式，位置更新时就可以保证始终在0和1两个量之间。

简单配电网，包含14个节点，13个常闭分段开关和2个常开联络开关。

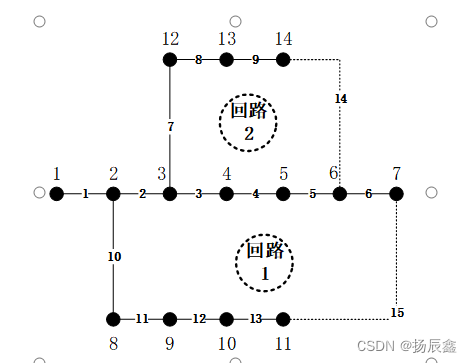
下面以该系统为例，说明二进制粒子群算法进行配电网重构的注意事项：

首先，如果在生成初始粒子时，如果不考虑拓扑约束，会出现大量的无效状态。在这里的配电网共有15个可操作开关，则系统的状态一共有2的15次方个，为32768，但如果随机生成状态，会出现大量孤岛或者环路的情况。因此，先确定系统中存在的两个回路，分别包含开关[2,3,4,5,6,10,11,12,13,15]和[3,4,5,7,8,9,14]，公共支路上的开关为[3,4,5]，总共的系统状态量为

，比所有的状态减少了将近90%，同时也提高了迭代效率。另外，在粒子迭代更新时，可以对迭代规则做一些改进，将每个回路中sigmoid函数值最小的开关置于断开状态，其余开关置于闭合状态，这样就保证了拓扑的有效性，提升算法的效率。目标函数可以选为系统网损最小。