一、LeetCode 343. 整数拆分
题目链接/文章讲解/视频讲解:https://programmercarl.com/0343.%E6%95%B4%E6%95%B0%E6%8B%86%E5%88%86.html
状态:已解决
1.思路
题目的要求是要我们拆除某个给定的整数,让其拆分后的数相乘结果最大。因此我们知道此题分两步,第一步是拆分,第二步是求乘积最大值。对于拆分,究竟是拆成两个数还是三个数还是四个数呢?弄清楚这点非常关键。
举个例子,对于9,我们是拆成3,3,3最大,这么一看,我们是要拆成三个数,而对于更大的数说不定还要拆成四五个数,好像很麻烦;然而,我们可以先不直接去拆9,而是从1开始拆起,当拆到6时,我们知道3*3=9是最大的,那么在这个前提下我们拆到9时,就不用拆成三个数,而是拆成3和6了,因为我们已知了6是还可以再拆的,并且6的拆分最大结果是9,那么拆成3和6的情况,其值其实为27而不是18!
由这个例子得到启发:拆数必须从小到大拆上来的,每次只需要拆成两个数,那么拆分结果就是前面保存的这两个数的拆分结果的最好值的相乘值(也就是说,这两个较小数前面已经被拆过了,我们只需要用它前面的拆分结果就行,不需要再去拆分了)!
(1)确定dp数组以及下标含义:
经过前面的分析,我们知道关键信息其实就是每个数的最好拆分结果,那么我们只需要用一个一维数组来保存它们就行了。
dp[i]:拆分数字i,得到的最大乘积为dp[i]。
(2)递推公式:
这一步其实就为刚刚思路的第二步,确定乘积最大值。要解决这个问题,就需要清楚乘积由哪几种情况产生。由于要从小到大得到到n的每个数的最好拆分结果,那么我们就需要一个外层循环i来遍历从1到n的每个数,内层循环j来对i进行拆分,拆成j和i-j。那么乘积的由来:
① j * (i - j) 直接相乘
② j * dp[i - j]
即,一个是原生拆两个数(确实拆成了两个数),另一个是表面拆两个数,实际是根据了两个数前面的拆分情况将i拆成了若干数(大于等于3)。
这里有个小细节是第二种拆法只拆了 i -j ,没有拆j。因为如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。所以递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
那么在取最大值的时候,为什么还要比较dp[i]呢?因为在递推公式推导的过程中,每次计算dp[i],取最大的而已。
(3)dp的初始化:
dp[2]初始化为1,这个很显而易见,但是dp[0]和dp[1]需要初始化吗?严格按照dp数组的定义来说是不需要的,因为0和1是不可拆分的,写上为了统一也无所谓。
(4)确定遍历顺序:
前面的分析已经说了,这道题是需要从小到大先n之内的数的最后拆分结果都求出来的,故遍历顺序肯定是从前往后。
(5)举例推导dp数组:
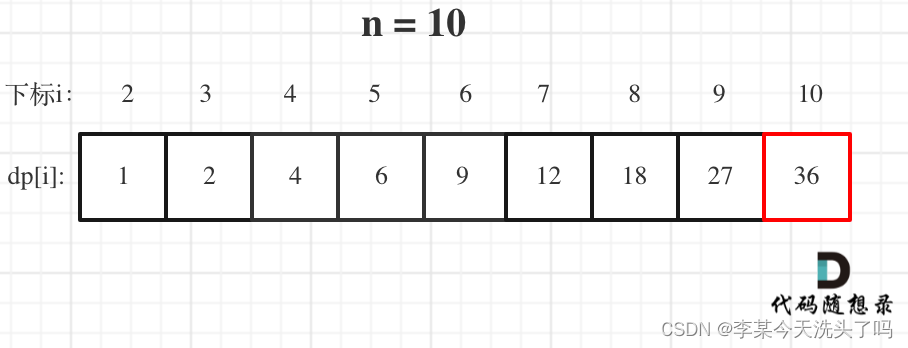
以 n=10 为例:
2.代码实现
class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1,0);dp[0]=1,dp[1]=1,dp[2]=1;for(int i=2;i<=n;i++){for(int j=1;j<=i/2;j++){//注意遍历到一半,超过这个值后面就是跟前面对称的了dp[i] = max(dp[i],max(j*dp[i-j],j*(i-j)));}}//打印结果// for(int i=1;i<=n;i++){// cout<<dp[i]<<" ";// }return dp[n];}
};
时间复杂度:O(n^2)
空间复杂度:O(n)
二、96.不同的二叉搜索树
题目链接/文章讲解/视频讲解:http:// 题目链接/文章讲解/视频讲解:https://programmercarl.com/0343.%E6%95%B4%E6%95%B0%E6%8B%86%E5%88%86.html 状态:已解决
状态:已解决
1.思路
首先,我们需要清楚一个二叉树的构成:左子树、中间结点、右子树。中间节点的左子树和右子树也都是一棵二叉树,意味着二叉树可以再分。这个结构是不是似曾相识!!我们知道动规问题也是可再分的:一个问题可以分解成若干的子问题,这也意味着一个问题实则由若干个子问题组成,跟二叉树由若干个左右二叉树组成的结构一样!因此,我们就可以类比地知道左右子树就是一个子问题,也就是说,我们要求一棵完整二叉树的构成,就是要在左右两棵子树的构成上,将二者再次合成一个二叉树,那么,一个完整二叉树的形态数就等于所有的左子树形态数*右子树形态数之和。
那么怎么分左子树和右子树呢?因为这里构造二叉树是根据二叉树的节点数来的,那么意味着左子树形态集合的不同就代表构成它们的节点数不同(n=3和n=5构造的左子树形态集合不同),因此,我们只需要控制每次构造左子树的节点数不同(右子树节点数也对应不同),就能得到n个节点所有可能的左子树形态集合。那么要怎样控制每次构成左子树的节点数不同呢?很简单,n个节点从左到右依次作为中间结点即可。
根据上述分析,得到动规五部曲:
(1)确定dp数组以及下标的含义:
因为我们只需要每个节点数对应的二叉树的形态数,故用一个一维数组保存信息就够了,dp[i]: i个节点构造的二叉树形态数为dp[i]。
(2)确定递推公式:
外层循环i代表以 i 为总结点数的二叉树,内层循环 j 代表在i个节点中,选取 j 作为中间结点。然后我们统计以 i 为总结点数的二叉树的总形态。
根据上面的分析,我们知道一个完整二叉树的形态数就等于所有的左子树形态数*右子树形态数之和。故dp[i] += dp[j - 1] * dp[i - j];
(3)初始化dp数组:
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。那么dp[0]应该是多少呢?从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。所以初始化dp[0] = 1。
(4)确定遍历顺序:
因为要求以n为总节点数的二叉树的总形态数,需累计各种左子树形态数*右子树形态数的和,也就是需要先知道以(i - j) 为节点总数的左子树的形态数和以(j - i)为节点总数的右子树的形态数,故要先知道n前面的节点数的总形态数,故应该从前往后遍历。
(5)举例推导dp数组:
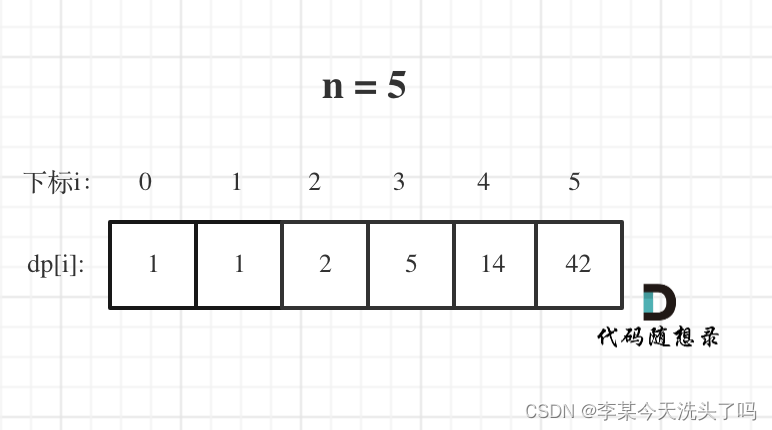
以n=5为例:
2.代码实现
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1);dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){dp[i] += dp[j-1]*dp[i-j];}}return dp[n];}
};时间复杂度:O(n^2)
空间复杂度:O(n)