引言

今天开始学习进阶版的 $DP$ 问题，还是按照知识点来分，按照题目来进行讲解，这个 $DP$ 问题尤其是算法竞赛是非常容易考的，因为感觉大部分的问题就是一个图论问题，也就是一个搜索问题，而 $DP$ 、网络流这种进阶问题其实就是对暴力枚举所有方案的一种优化，而且数据结构也只是为了某种操作进行的一种优化而已，所以说根本问题就是搜索，高级一点的就是剪枝和 $DP$ ，怪不得蓝桥杯老是考察这两样，因为本质上问题都是这两样。继续加油把！

闫氏DP分析法

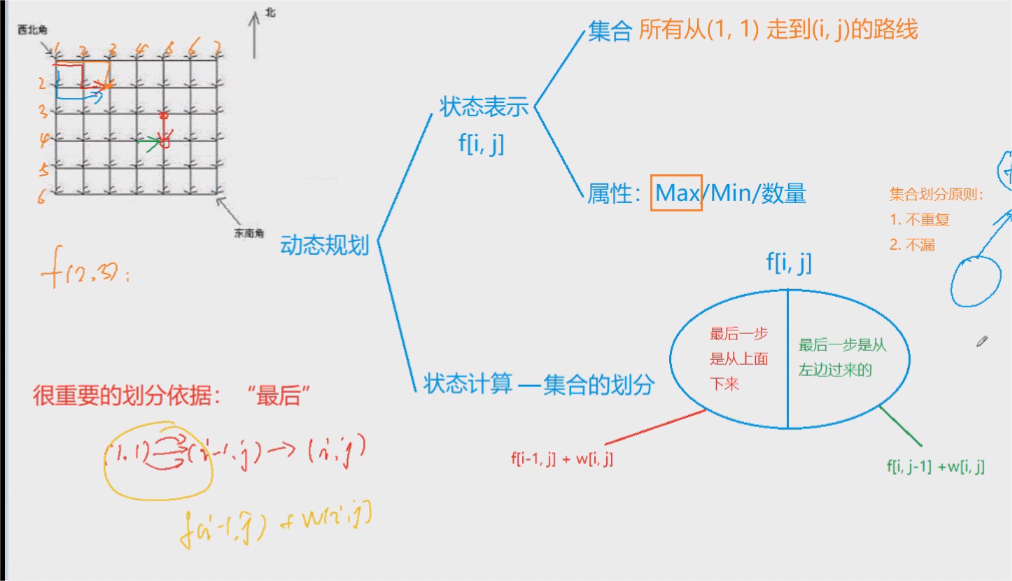
以摘花生这道题目为例：

• 首先要考虑状态表示：这通常是要靠经验的，也就是你做过类似的题都是怎么表示的，为什么DP问题要更快，因为它表示的是一个集合，而不需要把所有路径全部表示或者搜索。一般二维网格问题就是 $f[i][j]$ ，线性问题就是 $f[i]$ ，两个字符串问题就是 $f[i][j]$ ，背包问题就是 $f[v][w]$
• 属性：题目问什么，属性就是什么
• 集合的划分：通常是根据最后一步的不同来划分的
• 搜索顺序：按照拓扑序去搜，也就是说你的每一个状态所依赖的状态之前已经被计算过了
• 初始状态：根据你定义的状态表示，依据概念去初始化
  

---

一、摘花生

标签：DP、线性DP

思路：首先状态表示 $f[i][j]$ 代表从 $[1,1]$ 走到 $[i,j]$ 的所有路径集合中的最大值，状态计算可以从最后一步来考虑，要么是从上面走的，要么是从左面走的，所以状态转移方程为： $$f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j]$$ 然后就按照拓扑序来计算方程即可，关于拓扑序的理解：只要当前状态所依赖的上一个状态已经被计算过了，就可以了。然后初始状态就全为 $0$ 。

题目描述：

Hello Kitty想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。Hello Kitty只能向东或向南走，不能向西或向北走。问Hello Kitty最多能够摘到多少颗花生。输入格式
第一行是一个整数T，代表一共有多少组数据。接下来是T组数据。每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生
苗上的花生数目M。输出格式
对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。数据范围
1≤T≤100,1≤R,C≤100,0≤M≤1000
输入样例：
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例：
8
16

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 110;int n, m;
int w[N][N];
int f[N][N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);int T; cin >> T;while(T--){cin >> n >> m;for(int i = 1; i <= n; ++i){for(int j = 1; j <= m; ++j){cin >> w[i][j];}}for(int i = 1; i <= n; ++i){for(int j = 1; j <= m; ++j){f[i][j] = max(f[i-1][j], f[i][j-1]) + w[i][j];}}cout << f[n][m] << endl;}return 0;
}

---

二、最低通行费

标签：DP、线性DP

思路：首先有一个限制是必须在 $2\ast N-1$ 个时间单位内穿出去，如果我们考虑最优策略，只向下或者向右走，那么所需要的时间也就是 $2\ast N-1$ 了，所以这个时间翻译为只能向下向右走。然后状态表示就是 $f[i][j]$ 代表从 $[1,1]$ 走到 $[i,j]$ 所需要花的最小费用，然后状态转移方程就是 $f[i][j]=min(f[i-1][j],f[i][j-1])+w[i][j]$ ，然后这里值得注意的是，因为这个边界肯定是不能取得，比如说 $i,j$ 其中一个为 $1$ 的话，那么减一就是非法状态了，但是上一题没有特判是因为取的是最大值，非法的状态为 $0$ ，也就是说对于 $min$ 操作是不可能取到非法的状态的，所以本题也可以这样直接把所有的状态初始化为 $INF$ ，那么就去不到非法状态了。但是第一步得特判一下，上一题没有特判是因为刚好，所以不用。然后这种只能向右或者向下走的顺序，就按照一般的搜索顺序即可。

题目描述：

一个商人穿过一个 N×N 的正方形的网格，去参加一个非常重要的商务活动。他要从网格的左上角进，右下角出。每穿越中间 1 个小方格，都要花费 1 个单位时间。商人必须在 (2N−1) 个单位时间穿越出去。而在经过中间的每个小方格时，都需要缴纳一定的费用。这个商人期望在规定时间内用最少费用穿越出去。请问至少需要多少费用？注意：不能对角穿越各个小方格（即，只能向上下左右四个方向移动且不能离开网格）。输入格式
第一行是一个整数，表示正方形的宽度 N。后面 N 行，每行 N 个不大于 100 的正整数，为网格上每个小方格的费用。输出格式
输出一个整数，表示至少需要的费用。数据范围
1≤N≤100
输入样例：
5
1  4  6  8  10
2  5  7  15 17
6  8  9  18 20
10 11 12 19 21
20 23 25 29 33
输出样例：
109
样例解释
样例中，最小值为 109=1+2+5+7+9+12+19+21+33。

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 110;int n;
int w[N][N];
int f[N][N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){cin >> w[i][j];}}memset(f, 0x3f, sizeof f);for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){if(i == 1 && j == 1) f[i][j] = w[i][j];else f[i][j] = min(f[i-1][j], f[i][j-1]) + w[i][j];}}cout << f[n][n] << endl;return 0;
}

---

三、方格取数

标签：DP、线性DP

思路：首先是状态表示本来应该是 $f[i1][j1][i2][j2]$ 表示从 $[1,1]$ 到 $[i1][j1][i2][j2]$ 的两条路和的最大值，又因为是重复的只能算一次，所以就改为 $f[k][i1][i2],i1+j1=k,i2+j2=k$ ，减少了一维。然后就是状态转移方程了，集合的划分，最后一步，总共有四种状态为向右向下的组合，所以状态计算为 $$int\&v=f[k][i1][i2]$$$$v=max(v,f[k-1][i1-1][i2-1])$$$$v=max(v,f[k-1][i1-1][i2])$$$$v=max(v,f[k-1][i1][i2-1])$$$$v=max(v,f[k-1][i1][i2])$$ ，拓扑序就为正常正常的搜索顺序。

题目描述：

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。输入格式
第一行为一个整数N，表示 N×N 的方格图。接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。行和列编号从 1 开始。一行“0 0 0”表示结束。输出格式
输出一个整数，表示两条路径上取得的最大的和。数据范围
N≤10
输入样例：
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例：
67

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 15;int n;
int w[N][N];
int f[N * 2][N][N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;int a, b, c;while(cin >> a >> b >> c, a || b || c) w[a][b] = c;for(int k = 2; k <= n * 2; ++k){for(int i1 = 1; i1 <= n; ++i1){for(int i2 = 1; i2 <= n; ++i2){int j1 = k - i1, j2 = k - i2;if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){int& v = f[k][i1][i2];int t = w[i1][j1];if(i1 != i2) t += w[i2][j2];v = max(v, f[k-1][i1-1][i2-1] + t);v = max(v, f[k-1][i1-1][i2] + t);v = max(v, f[k-1][i1][i2-1] + t);v = max(v, f[k-1][i1][i2] + t);}}}}cout << f[n * 2][n][n] << endl;return 0;
}

---

四、传纸条

标签：DP、线性DP

思路：这道题跟上一道题是一道题，不一样的是该题是一个 $n\ast m$ 的矩阵，把这些细节改一下即可。

题目描述：

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排坐成一个 m 行 n 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直
接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 (1,1)，小轩坐在矩阵的右下角，坐标 (m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。 在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊
的时候就不会再帮忙，反之亦然。 还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 0 表示），
可以用一个 0∼100 的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。输入格式
第一行有 2 个用空格隔开的整数 m 和 n，表示学生矩阵有 m 行 n 列。接下来的 m 行是一个 m×n 的矩阵，矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度，每行的 n 个整数之间用空格
隔开。输出格式
输出一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。数据范围
1≤n,m≤50
输入样例：
3 3
0 3 9
2 8 5
5 7 0
输出样例：
34

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 55;int n, m;
int w[N][N];
int f[N * 2][N][N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= n; ++i){for(int j = 1; j <= m; ++j){cin >> w[i][j];}}for(int k = 2; k <= n + m; ++k){for(int i1 = 1; i1 <= n; ++i1){for(int i2 = 1; i2 <= n; ++i2){int j1 = k - i1, j2 = k - i2;if(j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m){int& v = f[k][i1][i2];int t = w[i1][j1];if(i1 != i2) t += w[i2][j2];v = max(v, f[k-1][i1-1][i2-1] + t);v = max(v, f[k-1][i1-1][i2] + t);v = max(v, f[k-1][i1][i2-1] + t);v = max(v, f[k-1][i1][i2] + t);}}}}cout << f[n+m][n][n] << endl;return 0;
}