题目
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
提示:0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
题解
这个问题可以使用动态规划来解决。我们可以定义一个二维数组dp,其中dp[i][j]表示将word1的前i个字符转换成word2的前j个字符所需的最少操作数。
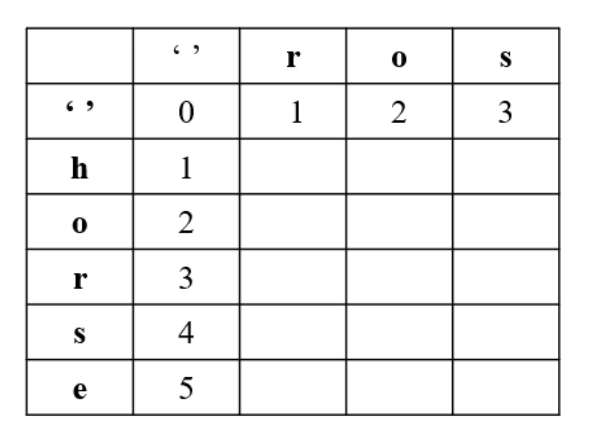
首先,我们需要初始化dp数组的边界条件。当word1为空字符串时,要将其转换成word2的前j个字符,需要进行j次插入操作;同样地,当word2为空字符串时,要将word1的前i个字符转换成空字符串,需要进行i次删除操作。因此,我们可以初始化dp数组的第一行和第一列如下:
dp[0][j] = j,对于所有的0 <= j <= word2.length()
dp[i][0] = i,对于所有的0 <= i <= word1.length()
接下来,我们可以通过填充dp数组的其余部分来求解最少操作数。我们可以遍历word1和word2的所有字符,对于每一对字符word1[i-1]和word2[j-1],我们可以进行以下操作:

如果word1[i-1]等于word2[j-1],则不需要进行任何操作,dp[i][j] = dp[i-1][j-1];
如果word1[i-1]不等于word2[j-1],则可以进行插入、删除或替换操作。我们可以选择其中操作数最小的一种,即dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1;
最后,dp[word1.length()][word2.length()]即为将word1转换成word2所需的最少操作数。
代码
public int minDistance(String word1, String word2) {int n = word1.length();int m = word2.length();// dp[i][j] 表示 word1 的前 i 个字母和 word2 的前 j 个字母之间的编辑距离int[][] dp = new int[n + 1][m + 1];// base casefor (int i = 0; i <= n; i++) {dp[i][0] = i;}for (int j = 0; j <= m; j++) {dp[0][j] = j;}// 自底向上求解for (int i = 1; i <= n; i++) {char c1 = word1.charAt(i - 1);for (int j = 1; j <= m; j++) {char c2 = word2.charAt(j - 1);if (c1 == c2) { // 相同字符,不需要操作dp[i][j] = dp[i - 1][j - 1];} else { // 不同字符,取三种操作的最小值dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;}}}return dp[n][m];
}
总结
上面的提供了一种使用动态规划解决将一个单词转换成另一个单词所需的最少操作数的算法。以下是算法的主要步骤:
- 初始化一个二维数组dp,其中dp[i][j]表示将word1的前i个字符转换成word2的前j个字符所需的最少操作数。
( 初始化dp数组的边界条件:当word1为空字符串时,要将其转换成word2的前j个字符,需要进行j次插入操作;当word2为空字符串时,要将word1的前i个字符转换成空字符串,需要进行i次删除操作。 - 遍历word1和word2的所有字符,对于每一对字符word1[i-1]和word2[j-1]:
- 如果word1[i-1]等于word2[j-1],则不需要进行任何操作,dp[i][j] = dp[i-1][j-1];
- 如果word1[i-1]不等于word2[j-1],则可以进行插入、删除或替换操作。选择其中操作数最小的一种,即dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1。
- 返回dp[word1.length()][word2.length()],即将word1转换成word2所需的最少操作数。
这个算法的时间复杂度为O(m×n),其中m和n分别是word1和word2的长度。通过动态规划的思想,我们可以高效地求解这个问题。