目录
数据流分析迭代的结束点就是到达了一个函数的不动点
偏序
上界和下界、上确界和下确界
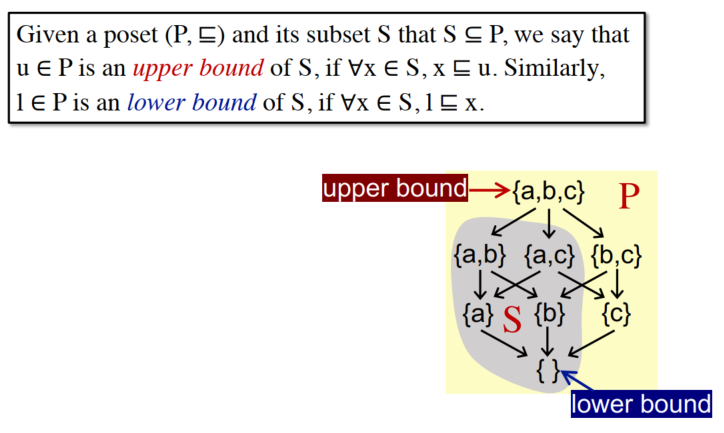
上界和下界
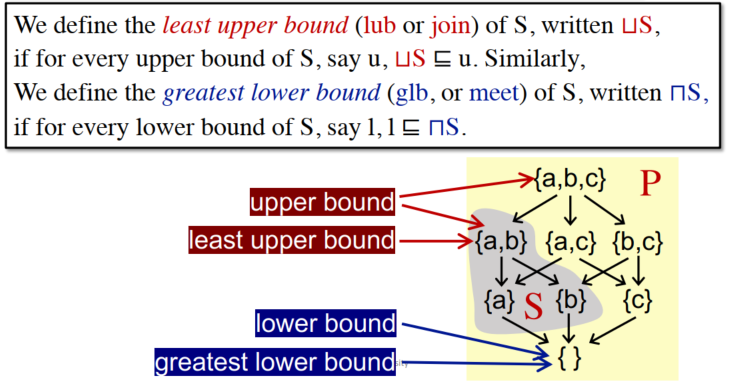
上确界和下确界
一些性质
格
半格
全格
product lattice
数据流分析和格
数据流分析的几个问题
第一问
第二问
第三问
lattice 上的单调性
lattice 不动点定理
证明我们求的不动点一定是最 小/大 不动点
迭代算法和不动点定理联系起来
常量分析
worklist algorithm
程序分析网课笔记,同步CSDN记录一下
网课链接:
南京大学《软件分析》课程05(Data Flow Analysis - Foundations I)_哔哩哔哩_bilibili
南京大学《软件分析》课程06(Data Flow Analysis - Foundations II)_哔哩哔哩_bilibili
数据流分析迭代的结束点就是到达了一个函数的不动点

偏序

理解一下为什么要叫做偏序

上界和下界、上确界和下确界
上界和下界
上确界和下确界

一些性质

格
一个偏序集的任意两个元素的最小上确界和最大下确界都存在,这个偏序集就是一个格
注意三个要素:
- 首先要是偏序集
- 其次是偏序集里任意找两个元素
- 这两个元素都要存在最小上确界和最大下确界

- 有穷的格是全格
- 但全格不一定都是有穷的格
半格
一个偏序集的任意两个元素的最小上确界和最大下确界只要存在一个,这个偏序集就是一个格

全格
这个在数据流分析里经常用,比较重要
一个格,格里的任意一个子集,这个子集的最小上确界和最大下确界都存在,则这个格就是全格——区别于格的定义
- 注意:这个子集的最小上确界和最大下确界不一定在这个子集里,但一定在这个格里

- 每个全格都有 top 和 bottom

- 每个有穷的格(即偏序集是有穷的)都是一个全格
-
- 下面的例子一里正整数集就不是有穷的
几个例子:


product lattice
给 n 个格,如果每个格的最小上确界和最大下确界都存在,那么就可以得出一个 product lattice:每个 lattice 的乘积
- 一个 product lattice 是一个格
- 如果一个 product lattice 中的每个格都是全格,则 product lattic 也是全格

数据流分析和格
数据流分析框架:(D,L,F)
D:方向,前向分析还是后向分析
L:格
F:转换函数

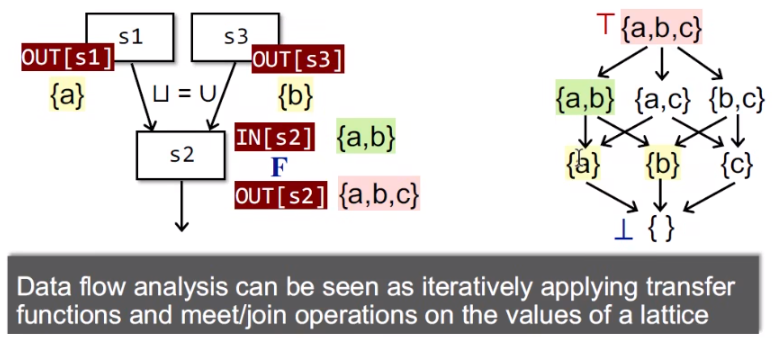
即:数据流分析就是在 lattice 上用 meet/join 操作+转换函数 不断地迭代的过程
数据流分析的几个问题

第一问
是的,因为转换函数里的 gen 和 kill 是不变的,out 不会缩小,只可能扩大
第二问
不动点可以有多个不动点,x=F(x)的时候就是就是不动点
但是我们的方法求的是不是最精确的那个不动点呢?这个是重点——是的
第三问
lattice 上的单调性
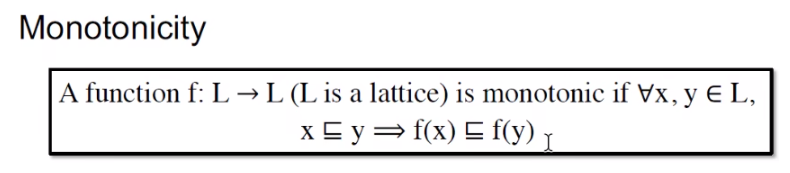
lattice 不动点定理

证明我们求的不动点一定是最 小/大 不动点
迭代算法和不动点定理联系起来
证明以下:通过将迭代算法和不动点定理联系起来


MOP 更精确,为什么不用?——太复杂了,要穷举所有完全路径,复杂,而且有的路径不会用到也要穷举,没必要
常量分析
must analysis
常量分析不满足 MOP,不满足可分配性

D:forworad,越往下越安全但也无用,但越往下也越不准(must 分析就是这样)
NAC 是很 safe 的,所有都不是常量,很安全,但是是 unless 的
常量传播的 domain 是一个个 pair(变量 x,x 的值)
meet operation 也不是简单的交或并
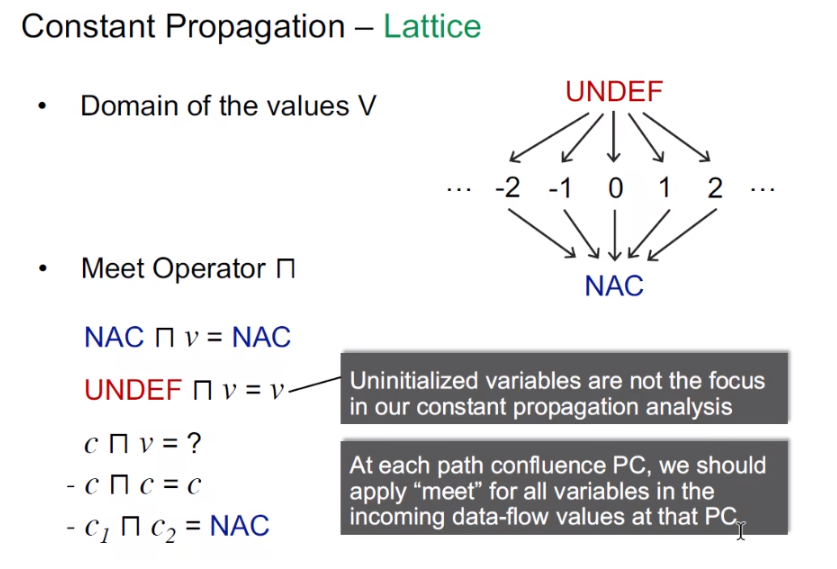
转换函数:

上面的(x, _)的 _ 意思是通配符,就是因为有 x=... 这个语句,那不管你到这儿前 x 是什么值,我都可以 kill 掉,所以用通配符
上面的最后一句意思是:如果压根儿没有赋值语句,比如都是条件跳转语句之类的,那我们这个转换函数就直接传入什么传出什么,是一个恒等( identity )函数

从上面例子可以证明常量传播是不可分配的
从上面例子也可以看出 MOP 是比我们的算法更精确的:
- must 分析越往下越不准
- 常量分析下面是 NAC,所以 c 的值来说,10 比 NAC 更准
- 而 NAC 是我们的算法求出来的,10 时 MOP 求出来的
worklist algorithm
是 iterative algorithm 的优化,比它更快
iterative algorithm 有很多冗余的计算:比如所有 out 里只有某一个 out 的一个位变化了(如 0 变为 1),但是却要把所有 basic block 的 out 都重新计算一遍

worklist algorithm 的优化就是:只重新 apply function 到 out 有变化basic block

初始时所有 basic block 都加入 worklist 中,开始 while 循环,worklist 为空时退出循环
while 循环内:
- 每轮循环都从 worklist 中拿出一个 bb(即 basic block)记作 B,并记录 B 现在的值,记作 old_OUT
- 然后 meet operator+transfer function apply 到这个 B,得到这个 B 的新的 OUT[B]
- 比较 apply 前后 B 的 out 值是否变化,如果变化了,说明这个 B 的后继的 out 都会变化,将 B 后继的 bb 都加入 worklist——为什么?因为这个 B 的 out 会作为其后继的 in,而如果一个 bb 的 in 没变那他的 out 就不会变(因为 gen 和 kill 固定),那如果 in 变了 out 自然也会变,而我们 worklist 就是关注那些 out 会变的 bb,所以要将 B 的后继 bb 都加入 worklist