目录
Reach Definition 可达分析
may analysis
算法
为什么会停?
活变量分析
may analysis: 不放过任何 path,v 在这条 path 上这条 path 就都要考虑
算法-后向传播
可用表达式分析
must analysis-不会误报,可能漏报
算法:前向传播
总结
程序分析网课笔记,同步CSDN记录一下
南京大学《软件分析》课程03(Data Flow Analysis I)_哔哩哔哩_bilibili
南京大学《软件分析》课程04(Data Flow Analysis II)_哔哩哔哩_bilibili
top
![]()
表示计算结果不确定,取值范围是全集
bottom
![]()
表示未定义,取值范围为空
may analysis:(over approximation)——meet 操作一般是 union 并
可能误报,但不会漏报,不放过任何一条运行时可能经过的路径
must analysis:(under approximation)——meet 操作一般是 join 交
不会误报,报出来的都是正确的,但可能漏报
Reach Definition 可达分析

may analysis
算法
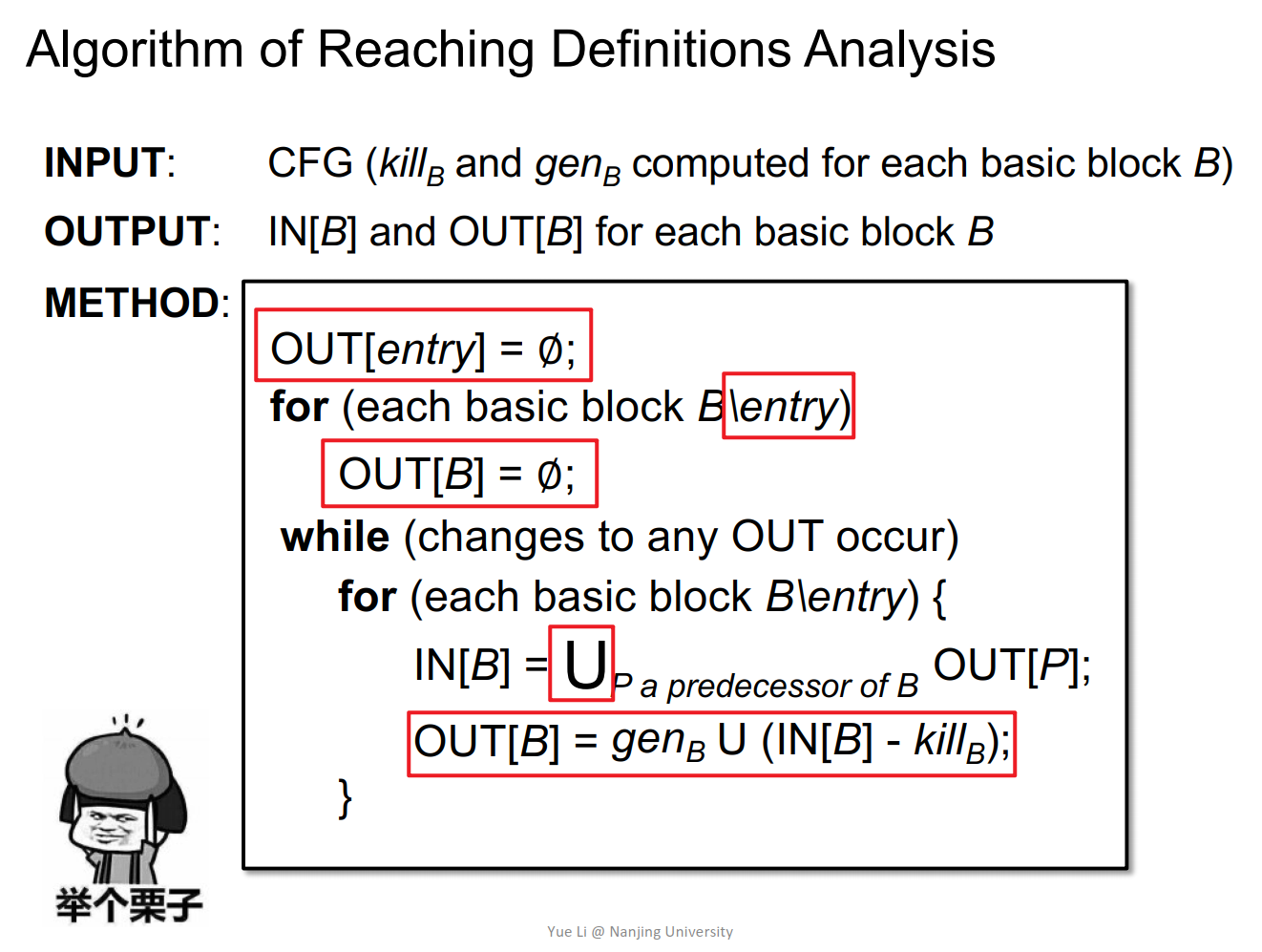
为什么会停?

活变量分析
may analysis: 不放过任何 path,v 在这条 path 上这条 path 就都要考虑

注意求活变量的点 p 在起始点,所以 backward 会更方便,从后往前的过程中分析到的信息直接往前传就好了,但是如果时从前往后,每次都要将分析到的信息传到 p 很麻烦
可以将 backward 算法得到的结果正向去验证了看:
- 某个程序点的活变量:该程序点到 exit 的所有路径中(——注意是到 exit完整的路径!),如果变量在重定义前使用了 或者 没有被重定义 那该程序点这个变量就是活的

算法-后向传播

可用表达式分析
must analysis-不会误报,可能漏报
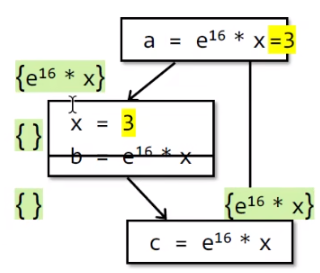
漏报的例子:上图假设重定义 x 后值不变,根据可用表达式算法分析,交集汇聚后会认为 e^16*x 的表达式不可用,但实际上是可用的,这就是漏报
可以用于检测全局共同子表达式

因为要保证所有路径都 evaluation 整个表达式,所以是交集

算法:前向传播

总结
三种分析过程及算法要清楚
是 may 还是 must
反正整个表都要背下来
domain含义:你的 data 是一堆什么?