作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。
会一些的技术:数据分析、算法、SQL、大数据相关、python
欢迎加入社区:码上找工作
作者专栏每日更新:
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化:企业实战案例
动态规划是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中极为重要的算法策略。它通过把复杂问题分解为简单子问题,以递推的方式逐步求解,大幅度提高了问题解决的效率。以下是对动态规划算法的详细介绍,包括其核心概念、步骤、以及通过具体例子来说明其应用。
1. 动态规划的核心概念
动态规划(Dynamic Programming, DP)是通过将复杂问题拆解成更小的子问题,并存储这些子问题的解(通常是在一个数组或矩阵中),从而避免重复计算,加快整体的计算速度。
关键特征:
- 最优子结构:一个问题的最优解包含其子问题的最优解。
- 重叠子问题:在求解过程中,很多子问题会被重复计算多次。
- 状态转移方程:每个状态都是前一个状态的函数,通过这些函数我们可以逐步求解出最终问题的答案。
2. 动态规划的基本步骤
步骤 1: 定义状态
首先定义“状态”,即原问题和子问题中会变化的部分。在大多数情况下,状态是一个或多个变量的函数。
步骤 2: 建立状态转移方程
状态转移方程是动态规划的核心,用于描述问题的递推关系。每个状态都是通过一个或多个前置状态计算得到。
公式

这意味着,如果当前背包的容量 w 足够装下第 i 件物品,我们将在不装这件物品和装了这件物品两种情况下取最大值;如果装不下,我们就保持装前 i-1 件物品时的最大价值。
步骤 3: 设定初始条件
根据问题的边界条件,确定状态数组的初值。对于一些问题,可能需要初始化多个状态值。
步骤 4: 执行状态填表
按照逻辑顺序,逐步填写状态表格。这个过程可以是自顶向下(带备忘的递归解法),也可以是自底向上(迭代解法)。
步骤 5: 构造最优解
根据填好的状态表格,构造问题的最优解。对于路径类问题,这可能还包括回溯状态表格。
3. 示例:0-1 背包问题
问题背景
0-1背包问题源于一个简单的概念:假设你是一个盗贼,打算抢劫一家商店。你有一个背包,它只能承载一定重量的物品。商店中有多种商品,每种商品都有一定的重量和价值。你的目标是在不超过背包承载重量的前提下,使背包中的物品总价值最大。
问题定义
- 输入:
- 整数 W,表示背包的最大承载能力。
- 列表
weights,其中weights[i]表示第 i+1 个物品的重量。 - 列表
values,其中values[i]表示第 i+1 个物品的价值。 - 整数 n,表示物品的总数。
- 输出:
- 背包能够承载的最大价值。
核心概念
- 状态表示:
dp[i][w]表示考虑前 i 个物品,当背包容量为 w 时的最大价值。 - 状态转移:
- 如果不选择第 i 个物品,则价值保持不变:
dp[i][w] = dp[i-1][w] - 如果选择第 i 个物品(前提是这个物品可以装入背包),则价值为装入该物品前的最大价值加上该物品的价值:
dp[i][w] = dp[i-1][w-weights[i-1]] + values[i-1] - 选择两者中的最大值:
dp[i][w] = max(dp[i-1][w], dp[i-1][w-weights[i-1]] + values[i-1] if w >= weights[i-1])
- 如果不选择第 i 个物品,则价值保持不变:
边界条件
dp[0][w] = 0对所有 w,因为没有物品时最大价值为0。dp[i][0] = 0对所有 i,因为容量为0时无法装入任何物品。
实际示例
假设有一个背包可以承载重量为50的物品,现有三件物品,具体信息如下:

解题过程
-
初始化动态规划表
dp。表格的大小为(物品数量+1) x (背包容量+1),即4 x 51。 -
填表过程:
-
根据表格,最终得出最大价值为
dp[3][50] = 220。
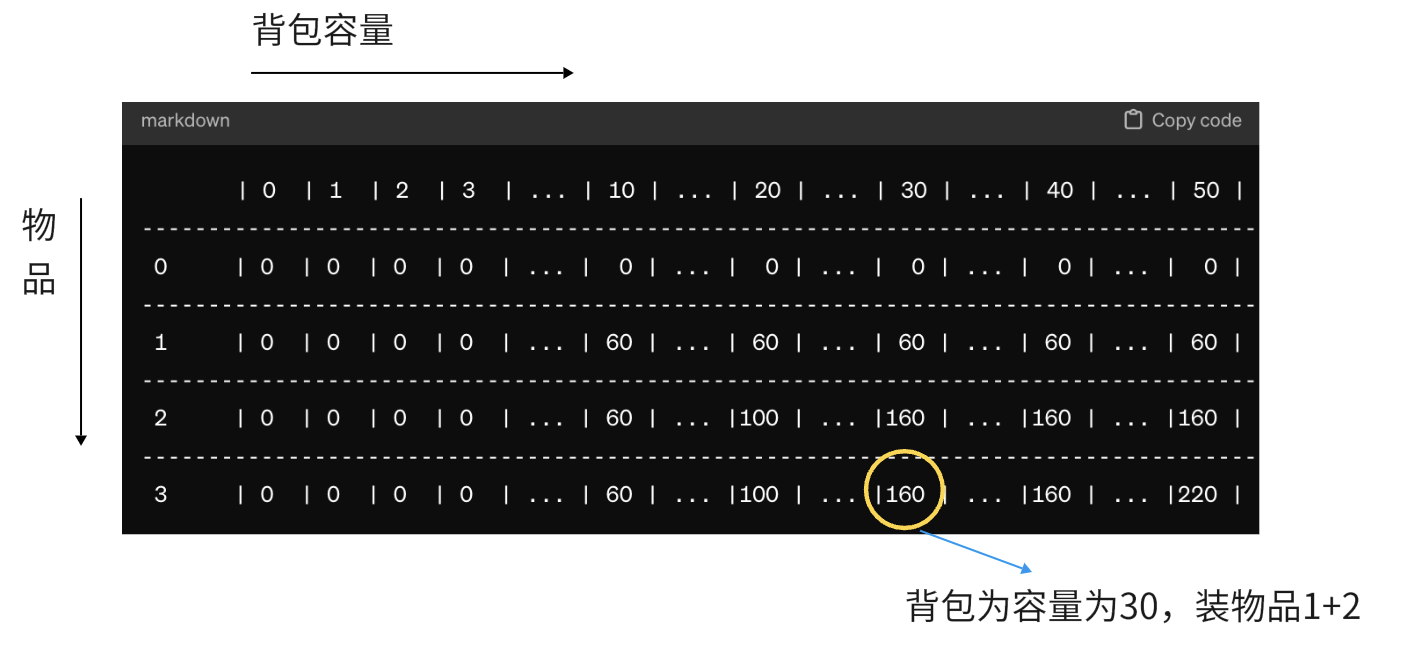
- dp[0][...] 是初始化为0的,因为没有物品时背包的价值自然也是0。
- dp[1][10] 到 dp[1][50] 是60,因为只考虑物品1时,只要背包容量至少为10,我们就能装下物品1,其价值为60。
- dp[2][20] 是100,因为如果我们只考虑物品1和2,并且背包容量至少为20,我们会选择物品2,因为它的价值(100)比物品1(60)更高。
- 当我们在 dp[2][...] 的基础上添加物品3考虑,如果背包容量是30,我们只能选择物品3(价值120),因为它的价值比物品1和2的组合更高。
- dp[3][50] 是220,这是因为在背包容量为50时,我们可以装下物品2和物品3(20 + 30 = 50),它们的价值总和(100 + 120 = 220)是这个容量下可能的最高价值。
代码实现
def knapsack(W, weights, values, n):dp = [[0 for x in range(W + 1)] for y in range(n + 1)]for i in range(1, n + 1):for w in range(1, W + 1):if w >= weights[i - 1]:dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1])else:dp[i][w] = dp[i - 1][w]return dp[n][W]# Test the function with the example data
weights = [10, 20, 30]
values = [60, 100, 120]
W = 50
n = len(weights)
print("The maximum value the knapsack can hold is:", knapsack(W, weights, values, n))