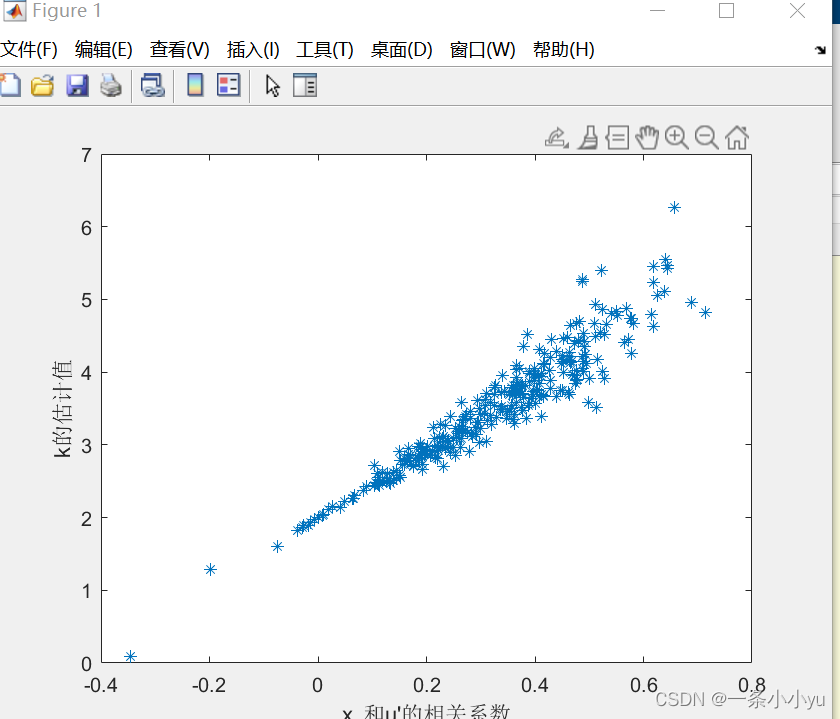
这是一个很好的例子,通过蒙特卡洛模拟展示了忽略相关变量时,回归系数估计的偏差。

%% 蒙特卡洛模拟：内生性会造成回归系数的巨大误差
times = 300;  % 蒙特卡洛的次数
R = zeros(times,1);  % 用来储存扰动项u和x1的相关系数
K = zeros(times,1);  % 用来储存遗漏了x2之后，只用y对x1回归得到的回归系数
for i = 1: timesn = 30;  % 样本数据量为nx1 = -10+rand(n,1)*20;   % x1在-10和10上均匀分布，大小为30*1u1 = normrnd(0,5,n,1) - rand(n,1);  % 随机生成一组随机数x2 = 0.3*x1 + u1;   % x2与x1的相关性不确定， 因为我们设定了x2要加上u1这个随机数% 这里的系数0.3我随便给的，没特殊的意义，你也可以改成其他的测试。u = normrnd(0,1,n,1);  % 扰动项u服从标准正态分布y = 0.5 + 2 * x1 + 5 * x2 + u ;  % 构造yk = (n*sum(x1.*y)-sum(x1)*sum(y))/(n*sum(x1.*x1)-sum(x1)*sum(x1)); % y = k*x1+b 回归估计出来的kK(i) = k;u = 5 * x2 + u;  % 因为我们回归中忽略了5*x2，所以扰动项要加上5*x2r = corrcoef(x1,u);  % 2*2的相关系数矩阵R(i) = r(2,1);
end
plot(R,K,'*')
xlabel("x_1和u'的相关系数")
ylabel("k的估计值")

主要思路是:

1. 生成自变量x1和x2,其中x2与x1有一定相关性
2. 生成依变量y,它与x1和x2都有线性关系
3. 假设我们在回归中只使用了x1,忽略了x2
4. 这时残差项中会包含被忽略的x2部分,因此残差项与x1就会产生相关性
5. 重复模拟多次,收集x1和残差的相关系数及只用x1回归估计的回归系数
6. 画出二者的散点图,可以明显看出相关系数越高,回归系数的偏差也越大

通过这个简单的模拟,很好地说明了忽略变量偏差的原理。这在计量经济学中是一个很经典的例子。