1.什么是回溯算法?
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。其本质是穷举,穷举所有可能,然后选出我们想要的答案。
2.为什么要有回溯算法?
那么既然回溯法并不高效为什么还要用它呢?
因为有的问题能暴力搜出来就不错了,撑死了再剪枝一下,还没有更高效的解法。比如下面这几类问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等。
3.如何理解回溯算法?
回溯法解决的问题都可以抽象为树形结构,是的,是所有回溯法的问题都可以抽象为树形结构!
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度就构成了树的深度。所以回溯和递归是分不开的。
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
4.回溯算法模板
类似递归算法的三部曲,回溯算法也有三部曲。
- 第一步:确认回溯函数的参数及返回值。返回值类型一般为void。但是参数不想二叉树递归那样好确定,所以一般先写逻辑,根据回溯代码逻辑的需要再添加相应参数。回溯函数大致长这样:
void backtracking(参数)- 第二步:确认回溯函数的终止条件。既然回溯函数的问题可以等效为树形结构,那么就会遍历树形结构就一定会有终止条件。因此回溯也有终止条件。一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。所以终止条件的伪代码如下:
if (终止条件) {存放结果;return;
}- 第三步:确认单层回溯的遍历过程
由于回溯一般是在集合中进行递归搜索,集合的大小构成了树的宽度,递归的深度构成了树的深度。如图所示:

回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归。
整体框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
力扣题目77.组合
77. 组合 - 力扣(LeetCode)![]() https://leetcode.cn/problems/combinations/description/
https://leetcode.cn/problems/combinations/description/
题目描述:
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ]
示例 2:
输入:n = 1, k = 1 输出:[[1]]
思路分析:
最直接的方法就是简单粗暴的双层循环(假设n=4,k=2):
int n = 4;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {cout << i << " " << j << endl;}
}这种k为2时就只用双层循环就行了,但是如果k=50,100?自己要写50层、100层循环就不太现实了。所以这个时候就可以使用回溯了。过程示意如图所示:

图中可以发现n相当于树的宽度,k相当于树的深度。
那么如何在这个树上遍历,然后收集到我们要的结果集呢?
图中每次搜索到了叶子节点,就找到了一个结果。
相当于只需要把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。
回溯解法:
来遍历的过程中,会找到复合要求的子集合,还要有记录这些子集合的结果大集合,所以下定义这两个记录结果的vector:
vector<vector<int>> result; //用于存放组合的集合
vector<int> path; //用于存放复合条件的当前组合下面按照回溯三部曲来进行回溯函数的实现:
- 第一步,确认回溯函数的参数以及返回值。
返回值为void,函数的参数为n,k。初次之外,为了更有逻辑的进行穷举,我们再设置一个startIndex,表示本次回溯从【1,2,..., n】的哪里开始遍历元素。所以回溯函数长这样:
void backtracking(int n, int k, int startIndex){
}- 第二步,确认回溯的终止条件。根据题意,当记录当前组合的path有了k个元素,即本次回溯就可以终止了,要保存当前结果然后返回。

具体回溯终止条件长这样:
//回溯第二步:确认回溯函数的终止条件
if(path.size() == k) //取得一个k长的组合
{result.push_back(path);return;
}- 第三步,确认单层回溯函数的遍历过程,即再回溯中需要做哪些事情?

根据上述伪代码,需要做三件事:1.在当前层处理节点,即将没遍历过程的元素记录一下;2.递归,从刚刚记录过的元素的下一个元素继续进行该过程,直到条件满足代码返回该递归处;3.弹出刚才最后记录的元素,相当于组合的结果返回来到了上一层的分支处(即通过绿色剪头回溯到示意图中的第二层):

代码如下:
//我要从startIndex往后开始遍历,将得到的节点元素存放在path中
for(int i = startIndex; i <= n; ++i)
{//处理节点path.push_back(i);//递归回溯函数,开始找下一个元素并添加到path中backtracking(n, k, i+1);//回溯,返回上一层path.pop_back();
}整体代码如下:
class Solution {
public:vector<vector<int>> result; //用于存放组合的集合vector<int> path; //用于存放复合条件的组合//回溯第一步:确认回溯函数的参数及返回值,//startIndex用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )void backtracking(int n, int k, int startIndex){//回溯第二步:确认回溯函数的终止条件if(path.size() == k) //取得一个k长的组合{result.push_back(path);return;} //回溯第三步:确认单层回溯的遍历过程。//我要从startIndex往后开始遍历,将得到的节点元素存放在path中for(int i = startIndex; i <= n; ++i){//处理节点path.push_back(i);//递归回溯函数,开始找下一个元素并添加到path中backtracking(n, k, i+1);//回溯,返回上一层path.pop_back();}}//力扣提供的接口函数vector<vector<int>> combine(int n, int k) {backtracking(n,k,1);return result;}
};从上述代码来理解,回溯算法的第三步中的递归,会一直执行,直到满足组合满足要求,然后会逐层进行回溯。

同样的回溯思想也可以解下面这道题。
257. 二叉树的所有路径
257. 二叉树的所有路径 - 力扣(LeetCode)![]() https://leetcode.cn/problems/binary-tree-paths/description/
https://leetcode.cn/problems/binary-tree-paths/description/
题目描述:
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
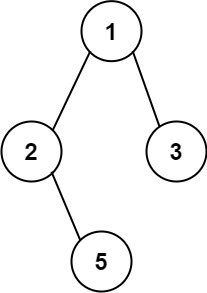
输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
思路分析:
因为要记录根节点到叶子节点的路径,所以二叉树的遍历方式应该为前序遍历,这样才是正确的路径顺序。遍历和和回溯的过程如下图所示,数字表示先后步骤。
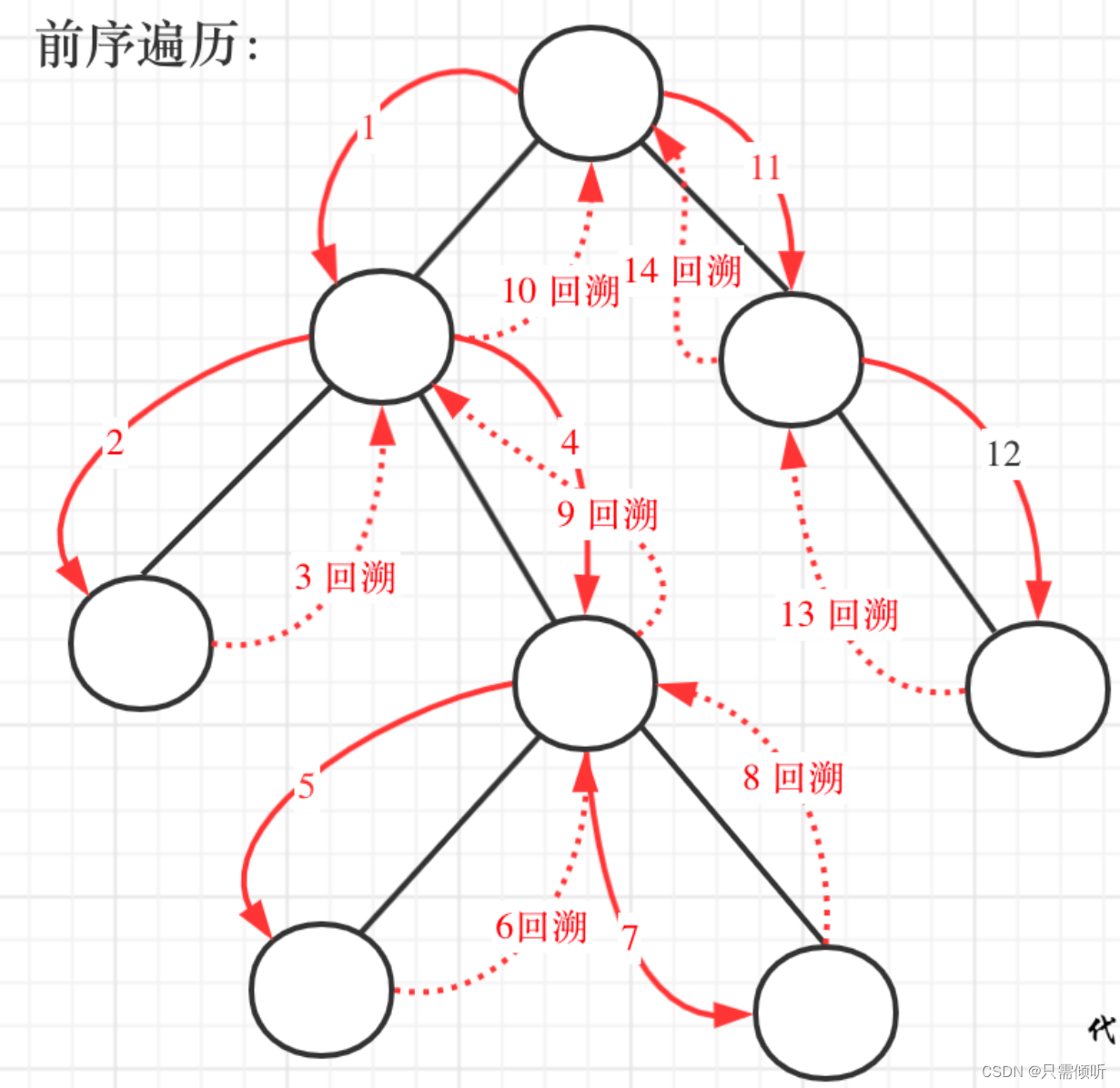
下面我们先使用递归的方式,来做前序遍历,然后在递归中使用回溯。
递归+回溯解法:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur, vector<int>& path, vector<string> & result){//中path.push_back(cur->val);// 递归终止条件:这才到了叶子节点if (cur->left == NULL && cur->right == NULL) {string sPath;for (int i = 0; i < path.size() - 1; i++) {sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]);result.push_back(sPath);return;}if (cur->left) { // 左 traversal(cur->left, path, result);path.pop_back(); // 回溯}if (cur->right) { // 右traversal(cur->right, path, result);path.pop_back(); // 回溯}}vector<string> binaryTreePaths(TreeNode* root) {vector<string> result; //记录路径的集合vector<int> path; //记录路径中的元素if (root == nullptr) return result;traversal(root, path, result);return result;}不使用额外的递归函数的写法:
class Solution {
public:vector<string> result; //记录路径的集合vector<int> path; //记录路径中的元素//前序递归第一步:确认递归函数的参数和返回值vector<string> binaryTreePaths(TreeNode* root) {if (root == nullptr) return result;path.push_back(root->val); //中,先记录一下当前节点元素//递归函数第二步:确认递归终止条件。找到叶子节点才算遍历结束if(root->left == nullptr && root->right == nullptr) {//一旦找到叶子节点,我们就需要打印该路径string singlePath;for(int i = 0; i < path.size()-1; i++) //从前往后提取路径“1-》2-》3”{singlePath += to_string(path[i]); //元素数字转字符串singlePath += "->";}singlePath += to_string(path[path.size()-1]); //最后一个元素result.push_back(singlePath); //记录该路径return result;} //递归第三步:确认单层递归逻辑。处了记录当前节点元素,接下来就是递归遍历左右子树了。//但是为了更方便的生成结果所需的字符串,我们将记录当前节点的步骤放在了函数的开头。//如果我们在这里记录当前节点元素,那么上面的递归终止条件返回的路径结果将会缺少最后一个元素//左if(root->left){binaryTreePaths(root->left); //递归遍历左子树path.pop_back(); //回溯,返回上一层对应的根节点,准备向右子树遍历}//右if(root->right){binaryTreePaths(root->right); //递归遍历右子树path.pop_back(); //回溯}return result;}};