在空间直角坐标系中,绘制指定平面方程的图形
版本说明:
20240413_V1.01:更正代码错误,并修改输入参数类型(测试用例得修改)
20240413_V1.00:初始版本
一、平面方程
基本形式为:A*X+B*Y+C*Z+D=0
例如:对于X+23=0的平面方程如下
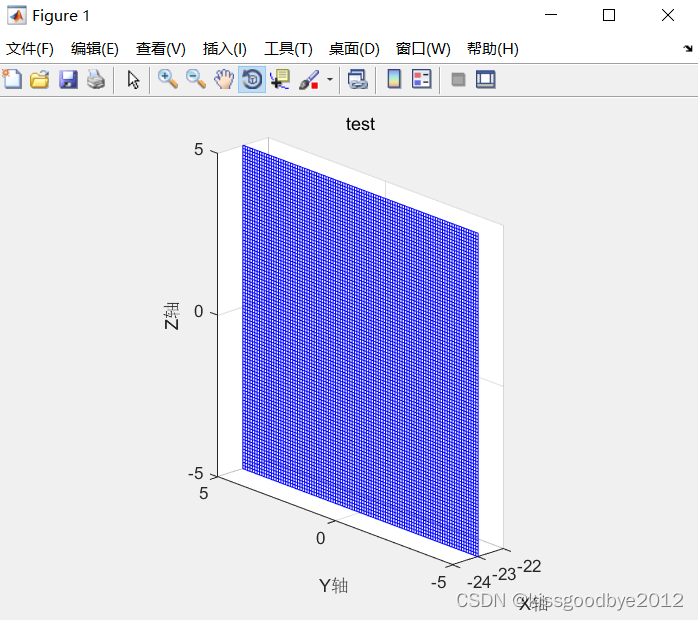
二、Matlab通用绘制函数
%% 绘制平面图形
% 输入参数:平面方程的参数以及图形的范围
function plot_plane(A, B, C, D, Range)
% 检查平面是否与坐标轴平行
if A == 0 && B == 0% 平面与z轴垂直[X, Y] = meshgrid(linspace(-Range, Range, 100),linspace(-Range, Range, 100));Z =zeros(size(X))-D; % 固定z值
elseif B == 0 && C == 0% 平面与y轴和Z轴平行[Y, Z] = meshgrid(linspace(-Range, Range, 100), linspace(-Range, Range, 100));X = zeros(size(Y))- D; % 固定X值
elseif A == 0 && C == 0% 平面与X轴和Z轴平行[X, Z] = meshgrid(linspace(-Range, Range, 100),linspace(-Range, Range, 100));Y = zeros(size(X))- D; % 固定x值
elseif C == 0% 平面与Z轴平行[X, Z] = meshgrid(linspace(-Range, Range, 100),linspace(-Range, Range, 100));Y = -(A.* X +D)/B; % 解平面方程得到Y
else% 平面不与Z坐标轴平行% 选择一个合适的范围来创建网格点[X, Y] = meshgrid(linspace(-Range, Range, 100),linspace(-Range, Range, 100));Z = -(A.* X + B.* Y+D)/C; % 解平面方程得到z
end% 绘制平面
surf(X, Y, Z, 'FaceColor', 'none', 'EdgeColor', 'blue');% 设置图形属性
grid on;
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
xlim([-Range, Range]);
ylim([-Range, Range]);
zlim([-Range, Range]);
% axis equal; % 保持轴的比例一致
view(3); % 设置三维视角
end三、测试用例
3.1 X+23=0
plot_plane(1, 0, 0, 23, '平面绘制示例')

3.2 Y+23=0
plot_plane(0, 1, 0, 23, '平面绘制示例')
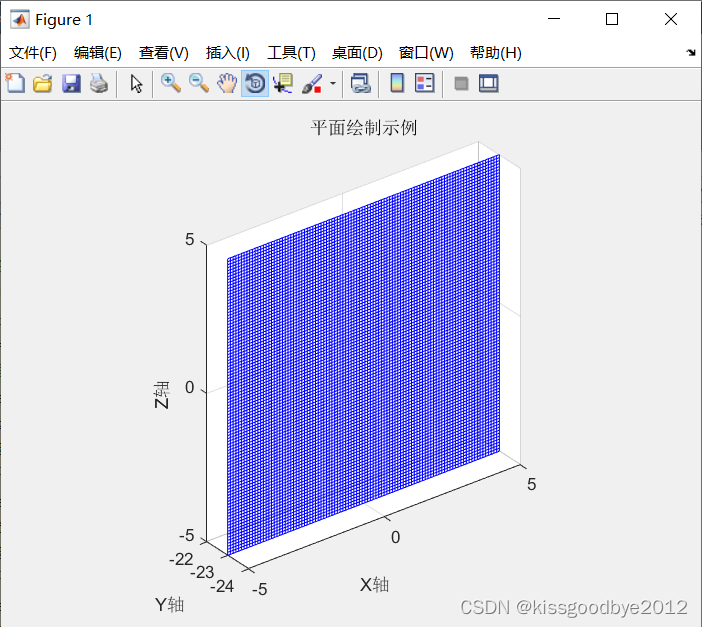
3.3 Z+23=0
plot_plane(0, 0, 1, 23, '平面绘制示例')

3.4 Y+Z+23=0
plot_plane(0, 1, 1, 23, '平面绘制示例')
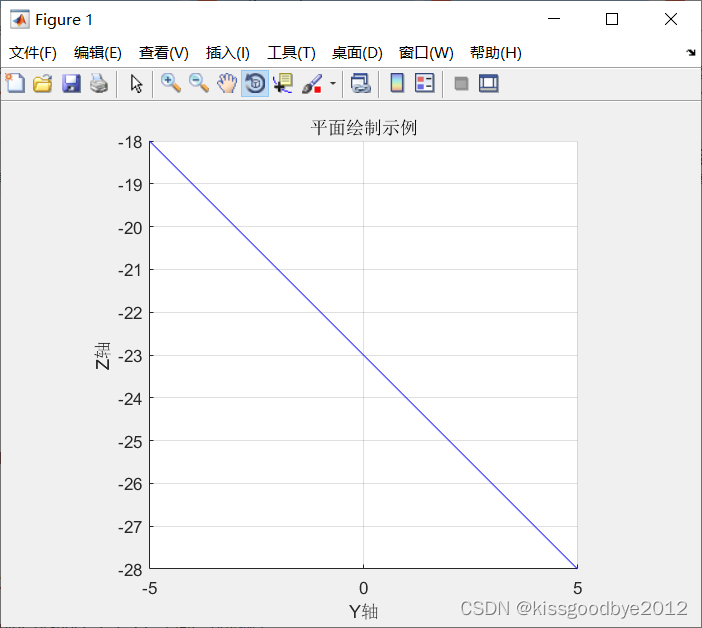
3.5 X+Z+23=0
plot_plane(1, 0, 1, 23, '平面绘制示例')
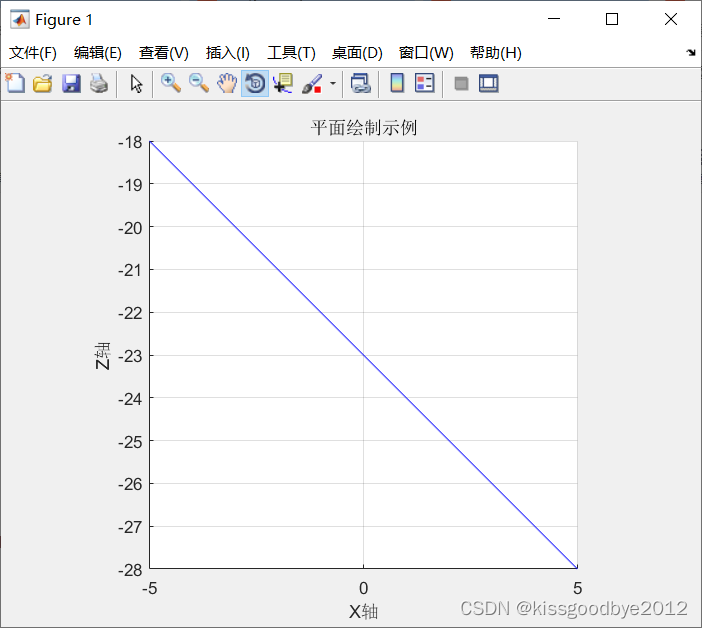
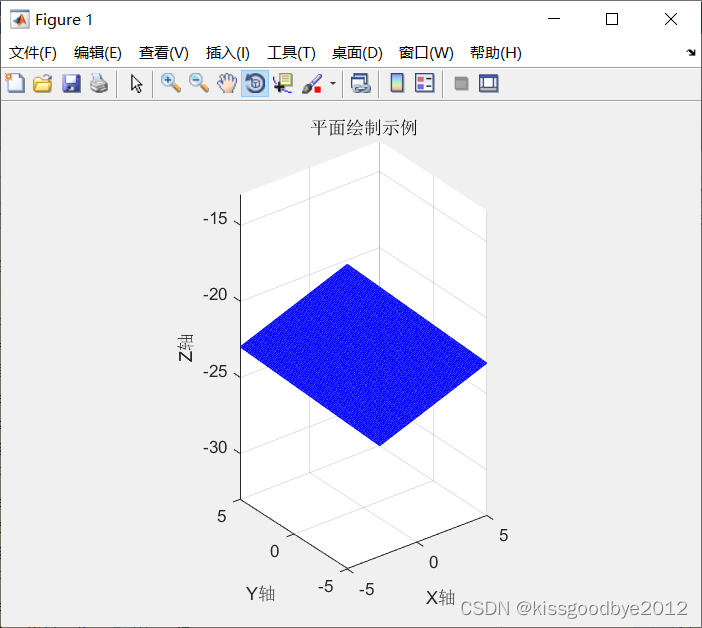
3.6 X+Y+23=0
plot_plane(1, 1, 0, 23, 5)

3.7 X+Y+Z+23=0
plot_plane(1, 1, 1, 23, '平面绘制示例')




![【YOLOv8改进[Neck]】使用BiFPN助力V8更优秀](https://img-blog.csdnimg.cn/direct/7462a827f58b4462b2a2c1196c550107.png)