概述
作为中国传统文化符号之一,太极八卦图,无论是哲学还是玄学,都不可能避开。
之前在ShapePoints函数库实现了太极的点求取函数。当时采用的时圆弧拼接的方式,但是存在某些尺寸下多边形无法三角化的问题。
于是就有了今天的内容。就是采取一种完全不同的思路来绘制太极。并在此基础上补足八卦的绘制。
太极图绘制的另一种思路
采用圆以及半圆逐层盖印的方式。可以避免原来的圆弧线无法三角化的问题。

基本上任何尺寸都不会有太大问题:

修改后的太极绘制函数:
# 太极 最后修改:2024年4月21日02:31:57
static func draw_taiji(canvas:CanvasItem, # 画布项position:Vector2, # 位置r:float,c1:= Color.BLACK,c2:= Color.WHITE,
) -> void:var T:= Transform2D().translated(position)var pan = T * ShapePoints.circle(r * 1.01 + 2)# 底部圆盘canvas.draw_colored_polygon(pan,c1)var r1 = ShapePoints.sector(r,90,270) # 左半大圆弧var r2 = ShapePoints.sector(r/2.0,90,270) # 左半小圆弧#print(right)canvas.draw_colored_polygon(T * r1,c2)canvas.draw_colored_polygon(T.translated(Vector2(0,r/2.0)) * r2,c1)canvas.draw_colored_polygon(Transform2D.FLIP_X.translated(position + Vector2(0,-r/2.0)) * r2,c2)var eye = ShapePoints.circle(r/10.0)canvas.draw_colored_polygon(T.translated(Vector2(0,r/2.0)) * eye,c2)canvas.draw_colored_polygon(T.translated(Vector2(0,-r/2.0)) * eye,c1)
八卦绘制
基础思路
- 只需要在太极周围围绕一圈卦就行。
- 其中阴阳爻,可以分别用
0和1代替,用类似[1,1,0]代表巽卦 - 用一个数组存储从
-90°到270°顺序的卦象。 - 然后根据这个数据进行绘制和变换。

实现
首先是定义卦象常数:
const QIAN = Vector3(1,1,1) # 乾
const XUN = Vector3(1,1,0) # 巽
const KAN = Vector3(0,1,0) # 坎
const GEN = Vector3(1,0,0) # 艮
const KUN = Vector3(0,0,0) # 坤
const ZHEN = Vector3(0,0,1) # 震
const LI = Vector3(1,0,1) # 离
const DUI = Vector3(0,1,1) # 兑
然后是卦象形状求取函数:
# 返回单独的卦的图形(多个矩形集合)
static func gua_shape(gua:Vector3,size:Vector2, # 卦的矩形尺寸
) -> Array[PackedVector2Array]:var shape:Array[PackedVector2Array] = []var rect = ShapePoints.rect(size) # 整个卦的矩形# 一爻占1/5高度,阴爻中间有1/5间隔var w = size.x # 爻的宽度var h = size.y/5.0 # 爻的高度var pos1 = Vector2(0 * w,2 * h) # 上爻位置var yang = ShapePoints.rect(Vector2(w,h)) # 阳爻var yin_harf = ShapePoints.rect(Vector2(w * 2/5,h)) # 阴爻的一半var yin = [Transform2D().translated(Vector2(-w * 0.3,0)) * yin_harf,Transform2D().translated(Vector2(w * 0.3,0)) * yin_harf]for i in range(3):var move := Transform2D().translated(pos1 - 2 * i * Vector2(0,h))if gua[i] == 0:shape.append_array([move * yin[0],move * yin[1]])else:shape.append(move * yang)return shape
这里采用的是在一个限定尺寸的矩形中通过位移来实现上中下三爻的定位。
- 因为
ShapePoints的rect()函数已经变成了从单位圆与变换求得的形式,所以ShapePoints.rect(size),就是整个卦象图形所在的矩形。 - 我将整个矩形划分为了5×5的网格,则上中下爻的高度和间隔都是1/5的矩形高度,阴爻的两个矩形宽度是2/5的矩形宽度,中间间隔为1/5的矩形宽度
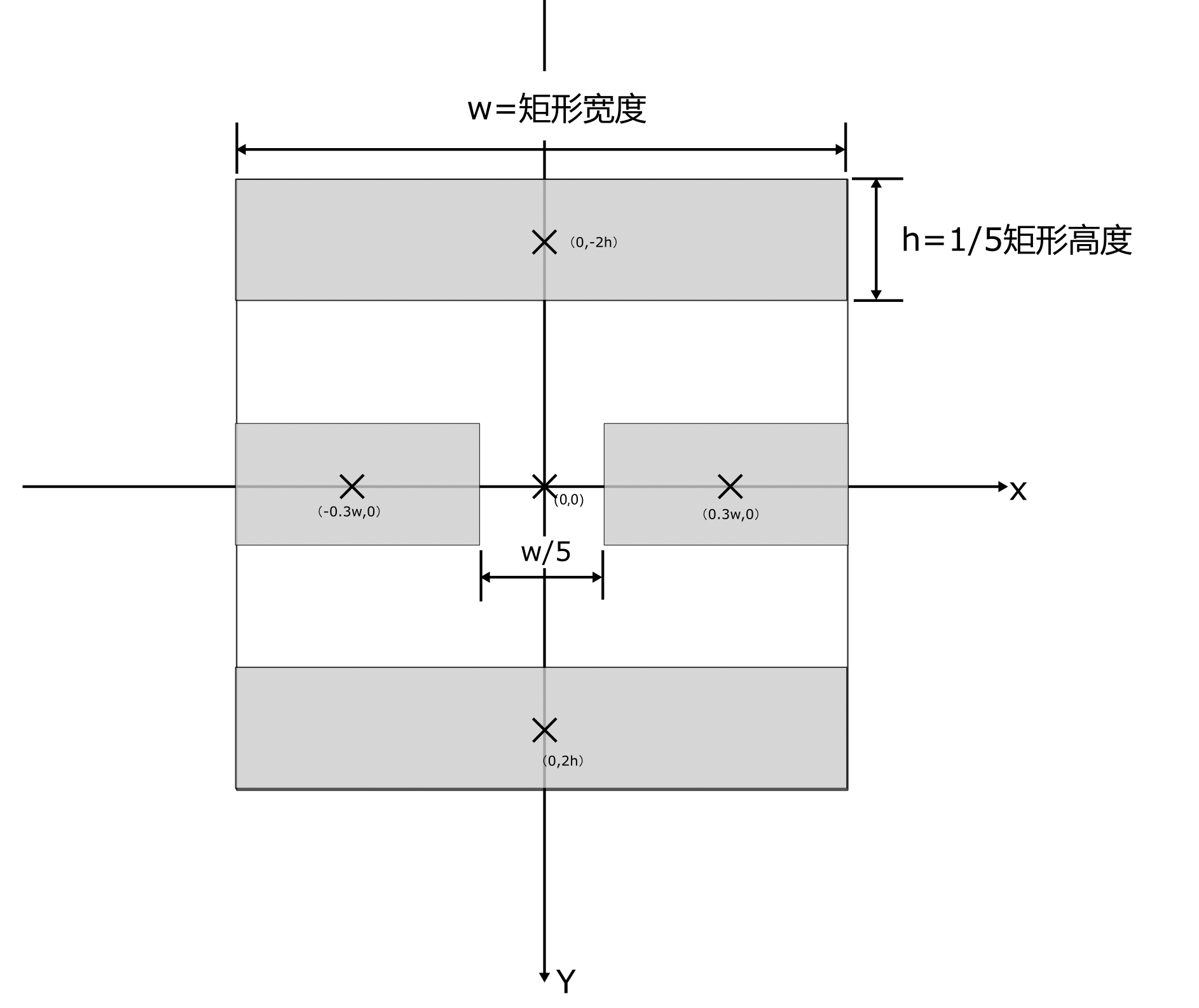
- 通过变换获取卦象在以原点为中心的图形集合后,就可以便利然后绘制。
最后是完整八卦绘制函数:
# 太极 最后修改:2024年4月21日13:03:25
static func draw_bagua(canvas:CanvasItem, # 画布项position:Vector2, # 位置size:Vector2, # 卦的矩形尺寸r:float,color:= Color.BLACK,bagua = [QIAN,XUN,KAN,GEN,KUN,ZHEN,LI,DUI]
) -> void:var ang = 360.0/8.0 # 间隔角度for i in range(bagua.size()):var t:= Transform2D().translated(Vector2(0,r)).rotated(deg_to_rad(ang * i -180))var shape = gua_shape(bagua[i],size) for sp in shape:canvas.draw_colored_polygon(Transform2D().translated(position) * t * sp,color)
八卦绘制,就是顺着一个圆的位置,顺序排布和旋转相应的卦象。
extends Node2Dvar pos = Vector2(200,200)func _draw() -> void:draw_set_transform(pos)# 绘制太极myCanvas.draw_taiji(self,pos,100)# 绘制八卦myCanvas.draw_bagua(self,pos,Vector2(40,40),140)
结合太极绘制函数,便可以绘制完整的太极八卦图了:

而且由于卦、八卦和太极三者对应三个函数,所以都可以分开来单独绘制。
总结
- 本节介绍了对复杂图形——太极八卦图的求图形顶点和绘制思路
- 可以看到,灵活的利用绘图顺序,进行“盖印”操作,是一种聪明的图形绘制方式
- 另外,也可以看到,有些复杂图形的求解需要使用多重线性变换。将原始的图形限定在一个中心点在原点的矩形或圆范围内,你将可以更好的创建由多个图形组成的复杂图形。再在此图形基础上进行其他变换获取更复杂图形。本文的八卦部分就是如此。