前面两道阅读理解直接跳过

C - Divide and Divide

大意

黑板上有一个数。

执行下列操作，直到黑板上的数全为1:

• 选择一个不小于2的整数，擦掉。
• 写下和。
• 需要的代价。

当不能继续操作时，总代价是多少？

思路

定义表示黑板上初始出现数字的代价，则有。

但是数很大，不能递推，需要记忆化搜索（有用的总状态数不会超过）。

使用map进行记忆化即可。

代码

#include <iostream>
#include <unordered_map>
using namespace std;typedef long long ll;
unordered_map<ll, ll> dp;ll dfs(ll x) {if (x < 2) return 0;if (dp.count(x)) return dp[x];return dp[x] = x + dfs(x / 2) + dfs((x + 1) / 2);
}int main() {ll n;cin >> n;cout << dfs(n) << endl;return 0;
}

D - Super Takahashi Bros.

大意

个关卡，初始只能玩第1关。

对于第关卡，有两种通关方式：

• 花费时间打完，跳到第关。
• 花费时间打完，跳到第关。

思路

转化为有向图，对于第关卡，

• 在点和点之间，建一条权值为的边。
• 在点和点之间，建一条权值为的边。

最后跑一遍从到的最短路即可。

代码

#include <iostream>
#include <queue>
#include <utility>
#include <cstring>
using namespace std;const int N = 2e5 + 9;
typedef long long ll;
typedef pair<ll, ll> pll;
ll n, a[N], b[N], x[N], dis[N];
bool vis[N];
priority_queue<pll, vector<pll>, greater<pll>> q;int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> n;for (ll i = 1; i <= n - 1; i++) cin >> a[i] >> b[i] >> x[i];memset(dis, 0x3f, sizeof dis);dis[1] = 0;q.push({ 0, 1 });while (q.size()) {auto t = q.top();q.pop();ll u = t.second;if (vis[u]) continue;vis[u] = true;ll v = u + 1;if (dis[v] > dis[u] + a[u]) {dis[v] = dis[u] + a[u];q.push({ dis[v], v });}v = x[u];if (dis[v] > dis[u] + b[u]) {dis[v] = dis[u] + b[u];q.push({ dis[v], v });}}cout << dis[n] << endl;return 0;
}

E - Mancala 2

大意

有个盒子，第个盒子有个球。

依次执行以下操作共次：

• 第次操作，将第个盒子的所有球均分，多余的球从第个盒子开始依次放一个。
• 如果处理到最后一个盒子还没放完，从第个盒子开始继续放。

问最后每个盒子的球数量。

思路

假设被取出球的盒子为，取出了个球，则放球时相当于：

• 先给每个盒子放个球
• 把剩下个球依次放入对应盒子。（注意分成两个部分算）

这是一个单点查询，单点修改，区间修改的操作，使用树状数组+差分维护即可。

代码

#include<iostream>
#include<vector>
using namespace std;
#define int long longtemplate<class T>
struct fenwick{vector<T> tr;int n;fenwick(int _n): n(_n){tr.resize(n + 1);}void add(int a, T b){while(a <= n){tr[a] += b;a += (a & -a);}}T ask(int a){T res{};while(a){res += tr[a];a -= (a & -a);}return res;}
};signed main(){ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int n, m;cin >> n >> m;fenwick<int> fwk(n + 1);for(int i = 1; i <= n; i++){int x; cin >> x;fwk.add(i, x);fwk.add(i + 1, -x);}while(m--){int x; cin >> x; x++;int y = fwk.ask(x);fwk.add(x, -y), fwk.add(x + 1, y);fwk.add(1, y / n), fwk.add(n + 1, -y / n);fwk.add(x + 1, 1), fwk.add(min(n, x + y % n) + 1, -1);if(x + y % n > n) fwk.add(1, 1), fwk.add(y % n - (n - x) + 1, -1);}for(int i = 1; i <= n; i++) cout << fwk.ask(i) << " ";return 0;
}

F - S = 1

大意

给定点，求一整数点，使得形成的三角形的面积为。

思路

画一张图：

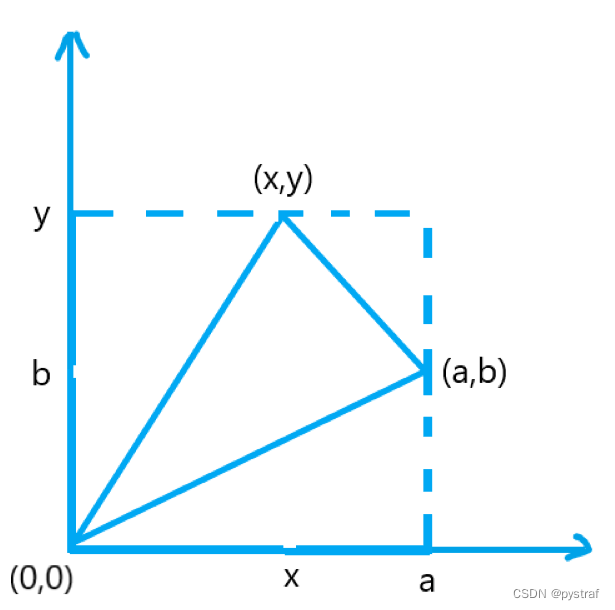
明显这个三角形面积等于这个长方形的面积减去周边三个小三角形的面积。

即

化简可得，但由于要考虑第二象限，所以应为

使用扩展欧几里德求的一组特解即可。

无解情况：如果，那么无解。

代码

#include<iostream>
using namespace std;
#define int long longint exgcd(int a, int b, int &x, int &y){if (!b){x = 1; y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= (a / b) * x;return d;
}signed main(){ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int x, y, a, b;cin >> a >> b;int d = exgcd(a, b, y, x);x = -x;if(2 % d) cout << -1 << endl;else{x = x * (2 / d);y = y * (2 / d);cout << x << ' ' << y << endl;}return 0;
}