Codeforces Round 940 (Div. 2) and CodeCraft-23 （A~E 最喜欢打表的一集）-编程知识

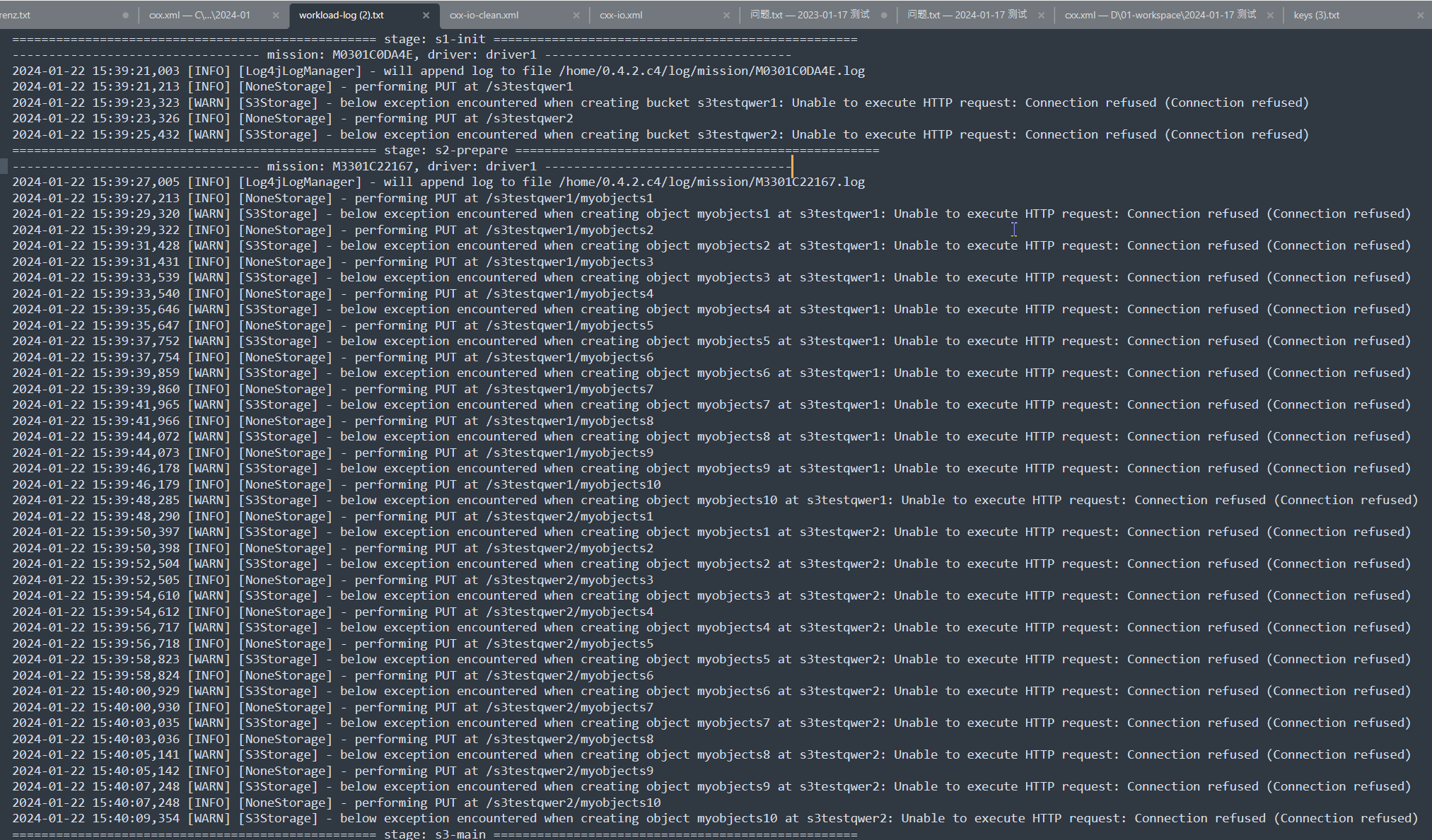
A - Stickogon

题意：给若干根长度不一的棍子，求能够组成的正多边形的最大个数。要求每个边只能用一个棍子。

思路：贪心，3个长度一样的棍子凑成一个正多边形，然后统计个数

void solve() 
{cin >> n;map<int ,int >mp;for(int i = 0 ; i < n ; i ++){int x;cin >> x;mp[x] ++;}	int ans = 0;for(auto it : mp){ans += it.second / 3;}cout << ans << endl;
}

B - A BIT of a Construction

题意：

思路：要求或运算1的个数最大，因此尽可能考虑每一位上的1都只出现一次，考虑位数越低的1代价越低，因此位数从小到大构造1，直到无法构造为止。

void solve() 
{cin >> n >> m;LL st = 1;if(n == 1){cout << m << endl;}else{int st = 1;while(st * 2 + 1 <= m){st = st * 2 + 1;}cout << st << " " << m - st <<" ";for(int i = 2 ; i< n ; i ++){cout << 0 <<" ";}cout << endl;}
}

C - How Does the Rook Move?

题意：

思路：当一个 $n*n$ 的棋盘上放上一颗棋子时，整行整列的棋盘都无法被访问，因此棋盘退化为一个空的 $(n-1)*(n-1)$ 的棋盘。因此可以想到用dp来求出 $n*n$ 的空棋盘能有多少种放法。

由于电脑会跟着你下，那么当你下了 $(r,c)(r\neq c)$ 时，电脑也会跟着下一步，整个棋盘退化为 $(n-2)*(n-2)$ 的空棋盘，当你下了 $(r,c)(r= c)$ 时，电脑不会下，棋盘退化为 $(n-1)*(n-1)$ 的空棋盘。接下来只需要考虑怎么从 $dp[i]$ 求出 $dp[i + 1]$ 即可。我们假设第一行第一列是新增的，然后考虑第一步放在每个地方的情况，发现下在 $(1,1)$ 的情况下会退化为 $i*i$ 的棋盘，其余情况都是 $(i - 1)*(i - 1)$ 的棋盘，因此状态转移方程有 $dp[i] = dp[i - 1] + (i + i - 2) * dp[i - 2]$ , 然后再根据输出判断出k步以后退化为多大的棋盘即可。

// Problem: C. How Does the Rook Move?
// Contest: Codeforces - Codeforces Round 940 (Div. 2) and CodeCraft-23
// URL: https://codeforces.com/contest/1957/problem/C
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
vector<int>dp(N , 0);
void solve() 
{cin >> n >> m;for(int i = 0 ; i < m ; i ++){int x , y;cin >> x >> y;if(x == y){n -= 1;}else{n -= 2;}}cout << dp[n] << endl;
}            
signed main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;dp[0] = 1;dp[1] = 1 , dp[2] = 3;for(int i = 3 ; i < N ; i ++){dp[i] = 1 * dp[i - 1] + (i - 1) * 2 * dp[i - 2];dp[i] %= mod;}cin>>t;while(t--){solve();}return 0;
}

D - A BIT of an Inequality

思路：为了方便表示，我们记 $a_{i , r} = a_{l} \oplus a_{l + 1} \oplus....\oplus a_{r}$ 。如果我们钦定 $a_{y}$ , 所求数即需要满足 $a_{l , r} \oplus a_{y} > a_{l , r}$ 。再根据异或运算的性质：不进位加法，可以发现：假设 $a_{y}$ 的最高位为第x位， $a_{l , r}$ 的第x位是0的话，就能够满足题意，因此我们需要统计的是：以 $a_{y - 1}$ 为结尾的区间的各个位的奇偶数情况以及 $a_{y +1}$ 开头的区间的各个位的奇偶数情况，然后再将两者结合即可。

void solve() 
{cin >> n;for(int i = 1 ; i <= n ; i ++){cin >> a[i];}int dp1[n + 5][32][2];//i结尾的int dp2[n + 5][32][2];//i开头的memset(dp1 , 0 , sizeof dp1);memset(dp2 , 0 , sizeof dp2);for(int i = 1 ; i <= n ; i ++){for(int j = 0 ; j < 32 ; j ++){if((a[i] >> j) & 1){dp1[i][j][1] = dp1[i - 1][j][0] + 1;dp1[i][j][0] = dp1[i - 1][j][1];}else{dp1[i][j][1] = dp1[i - 1][j][1];dp1[i][j][0] = dp1[i - 1][j][0] + 1;}}}for(int i = n ; i >= 1 ; i --){for(int j = 0 ; j < 32 ; j ++){if((a[i] >> j) & 1){dp2[i][j][1] = dp2[i + 1][j][0] + 1;dp2[i][j][0] = dp2[i + 1][j][1];}else{dp2[i][j][1] = dp2[i + 1][j][1];dp2[i][j][0] = dp2[i + 1][j][0] + 1;}}}	LL ans = 0;for(int i = 1 ; i <= n ; i ++){//ai为中间值for(int j = 32 ; j >= 0 ; j --){if((a[i] >> j) & 1){//左侧+右侧=奇数ans += dp1[i - 1][j][0] * dp2[i + 1][j][1];ans += dp1[i - 1][j][1] * dp2[i + 1][j][0];ans += dp1[i - 1][j][1];ans += dp2[i + 1][j][1];break;}}}	cout << ans << endl;
}

E - Carousel of Combinations

题意：

思路：若不取模，可以发现 $C(i,j) = c(i , j) * f[j] / j$ ，其中 $c(i , j)$ 从i个里面选出j个数的排列， $f(j)$ 表示j个数的组合，然而由于可以旋转匹配，所以j个序列合为1个序列。

然后打表发现：当j为素数时， $C(i , j)$ 的规律：随着 $i$ 的增大依次为 $j$ 个 $(j -1) \ mod\ j$ , $j$ 个 $(j -2) \ mod\ j$ ..当 j 为4时较为特殊，可自行打表。然后就是一个简单的求和了。

// Problem: E. Carousel of Combinations
// Contest: Codeforces - Codeforces Round 940 (Div. 2) and CodeCraft-23
// URL: https://codeforces.com/contest/1957/problem/E
// Memory Limit: 256 MB
// Time Limit: 2500 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 1e06+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
vector<LL>prime;//存储素数
bool vis[N+5];
void su() 
{for(int i=2;i<=N;i++){if(!vis[i])prime.pb(i);for(int j=0;j < prime.size() && prime[j] * i <= N;j ++){vis[prime[j]*i]=1;if(i % prime[j]==0)break;}}
} 
LL qpow(LL a , LL b)//快速幂
{LL sum=1;while(b){if(b&1){sum=sum*a%mod;}a=a*a%mod;b>>=1;}return sum;
}
LL f[N] , g[N];
void init(){f[0] = g[0] = 1;for(int i=1;i < N; i ++){f[i]= f[i-1] * i % mod; //计算i的阶乘g[i] = g[i-1] * qpow(i , mod - 2) % mod; //计算i的乘法逆元 qpow为快速幂}
}
LL get(int n,int m ){ //得到C(n,m)的组合数答案if(n < m)return 0;elsereturn f[n] * g[m] % mod * g[n-m] % mod;
}
LL cnt(int x , int y){LL res = get(x , y) * f[y - 1];res %= y;return res;
}
vector<int>add(N + 5 , 0);
vector<int>dp(N + 5 , 0);
void solve() 
{for(auto it : prime){int now = it - 1;add[it] += now;for(int st = it * 2 ; st < N ; st += it){if(now > 0){add[st]--;now--;}else{now = it - 1;add[st] += it - 1;}}}int now = 2;add[4] += 2;for(int st = 4 * 2 ; st < N ; st += 4){if(now > 0){add[st] -= 2;now -= 2;}else{now = 2;add[st] += 2;}}int cnt = 0;dp[0] = 0;for(int i = 1 ; i < N ; i ++){cnt += add[i];dp[i] = dp[i - 1] + cnt;dp[i] %= mod;}
}          
void win(){int n;cin >> n;cout << dp[n] << endl;
}  
signed main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);su();int t=1;init();cin>>t;solve();while(t--){win();}return 0;
}