学习笔记记录

1 树

&emsp；什么是树?树是一种非线性的结构，树和子树是相对的概念，例如A的子树有B，C，D。但是B的子树有E，F，因此相对于E，F而言，B也是一棵树，即在树的定义中又用到树的定义，其结构定义是一种递归的定义，它道出了树的固有特性，类似于下图：

1.1 树的描述（基本术语）

 有了树的结构，但是我们怎么描述这个树呢？而且要通俗易懂，所以术语就应运而生：

2 二叉树（树的度最大为2）

   二叉树本身就是树的一种，所以上面的树的术语完全适用于二叉树。

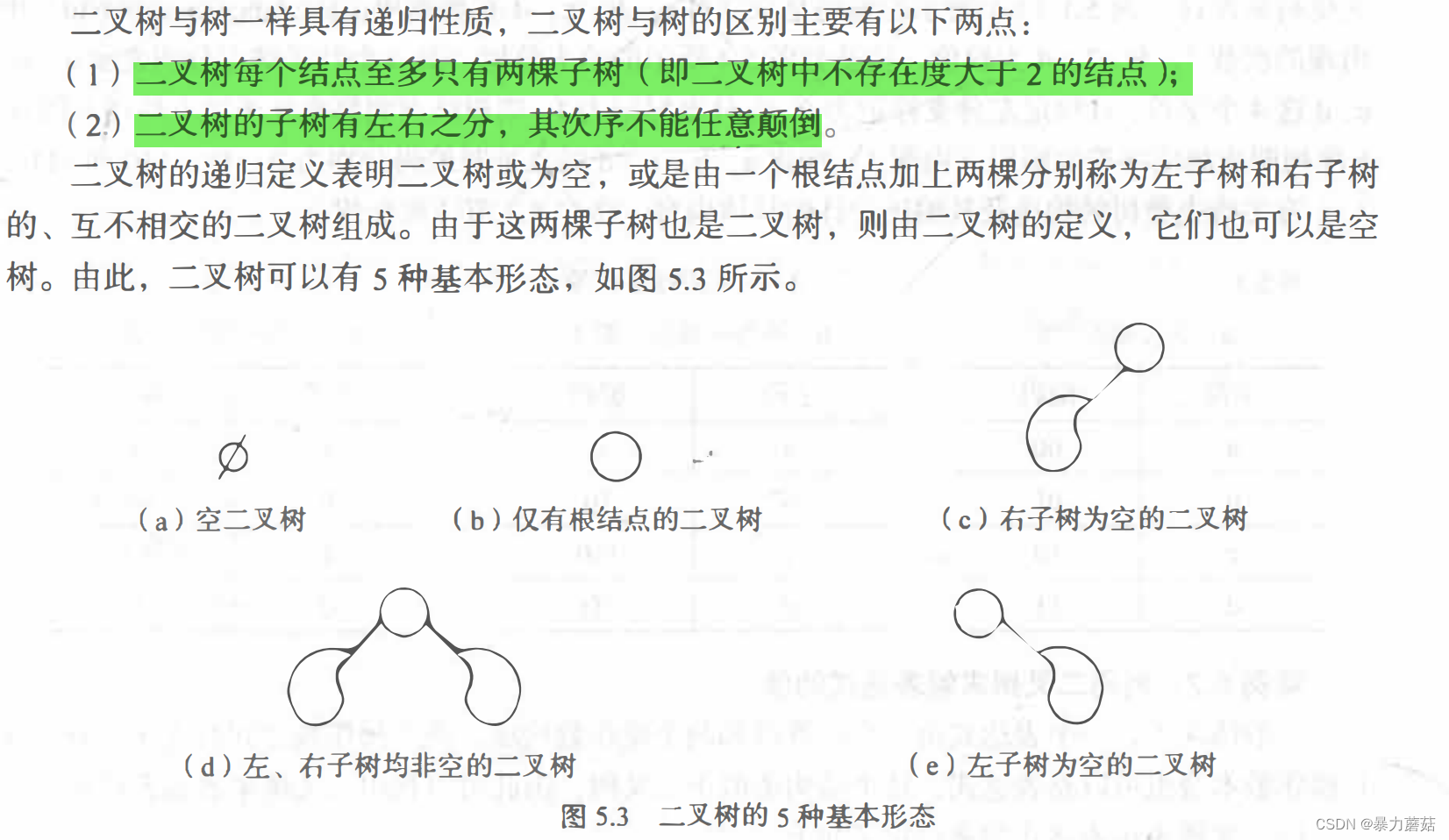
2.1 注意事项-五种基本形态

2.2 二叉树的抽象数据类型定义

 一般包三个方面：
 ADT BinaryTree{
 数据对象D：…
 数据关系R：…
 数据操作P：重点：}

3 二叉树的性质

• 在二叉树的 第i层上至多有$2^{i-1}$个结点.
• 深度为k的 二叉树至多有$2^k-1$ 个结点 (k>=1).
• 对任何一棵二叉树T, 如果其终端结点数（叶子）为n0，度为2的结点数为n2,则$n_0=n_2+1$。（证明）

1.对于整个树就是由度为0（叶子），度为1，度为2的节点组成，也就是
$$n=n_0+n_1+n_2.$$

2.而且n0节点射出0条线，n1节点射出1条线，n2 节点射出2线，则总的射出线条是:
$$\begin{array}{rl}{n}_{out}& =0\ast n_0+1\ast n_1+2\ast n_2\\ & =1\ast n_1+2\ast n_2\end{array}$$
3.对于每个节点而言，除了根节点，每个节点都会被插入一条线，所以：节点数n=插入的总线数+1
$$\begin{array}{rl}n& =n_{in}+1\end{array}$$
4.插入总线数=射入总线数=n1+2*n2;
$$\begin{array}{rl}{n}_{in}& =n_{out}\end{array}$$
5.可以得到：
$$\begin{array}{rl}n& =n_0+n_1+n_2=n_{in}+1=n_{out}+1=n_1+2n_2\end{array}$$
即：$n_0=n_2+1$

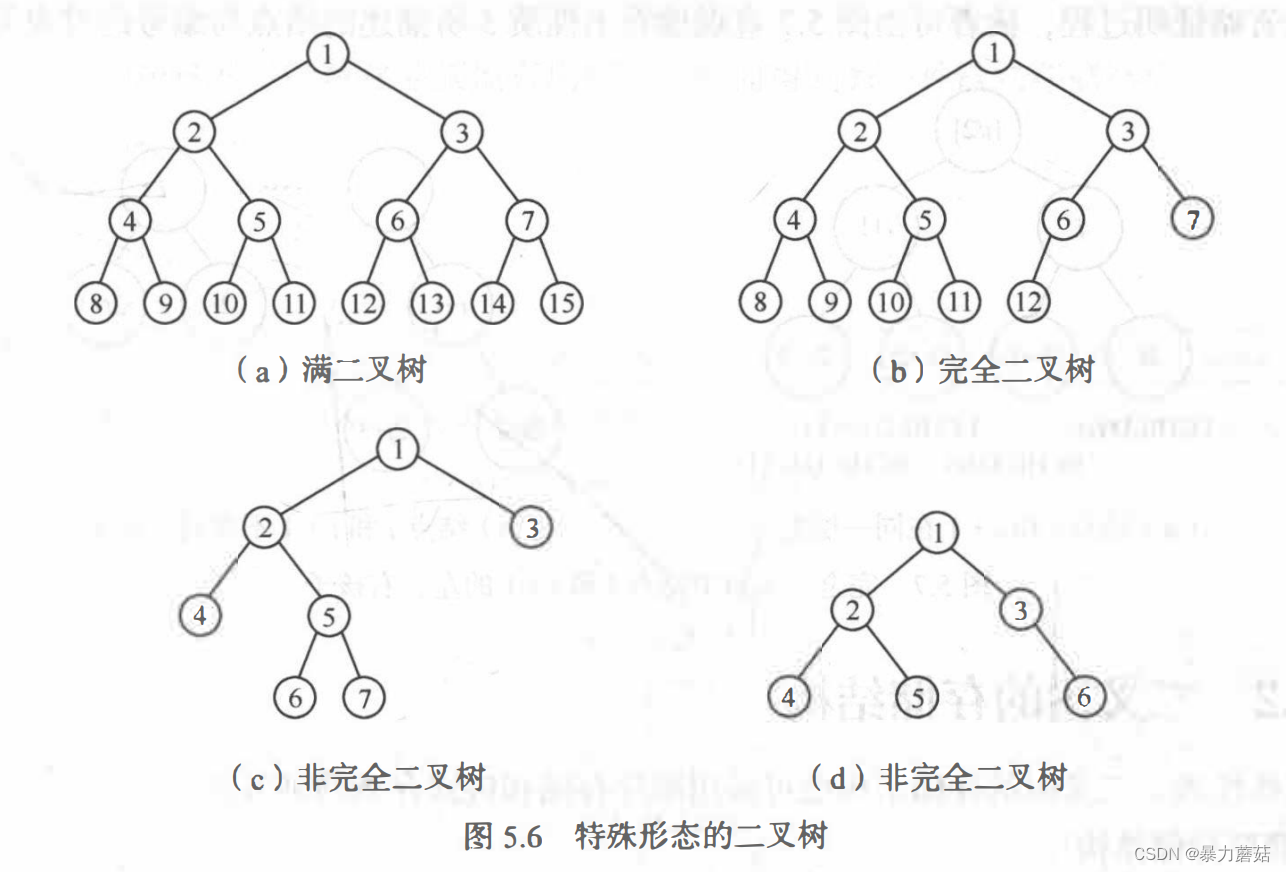
3.1 两种特殊形式的二叉树-重点会计算

• 例如：完全二叉树有节点1001个，求叶子节点有多少个？，注意n1只有两种情况，n1=1或者n1=0;

3.2 题目练习：

哈夫曼树没有度为1的节点，也就是n1=0;

4 二叉树的存储结构

4.1 顺序存储结构

  适合完全二叉树，由二叉树的性质可知，由一个节点 i 我们可以找到他的双亲，左右子节点；如下图：i=1时，直接没有双亲算根节点；例如现在有一个i=2的节点，让你找他的双亲肯定是i/2=1;找他的左孩子就是2i=4，右孩子就是2i+1=5；想一个问题？为什么i的右边是i+1,而 i 的下一层是2i？
这个是因为其是2叉树，层与层之间的关系一定是2倍的关系，所以对于三叉树，也可以有类似的性质，不过对于三叉树而言，其3i是位于中间；

非完全二叉树也可以用顺序存储结构进行存储，不过会浪费存储空间；

4.2 链式存储结构

  二叉树的链表中的结点至少包含 3 个域：数据域和左、 右指针域，如图 5.9 (b) 所示。有时，为了便于找到结点的双亲，还可在结点结构中增加一个指向其双亲结点的指针域.

5 遍历二叉树和线索二叉树

5.1 一般是三种遍历顺序（先左后右）

  有先序DLR，中序LDR，和后续LRD的三种遍历方式；这里拿中序举例，对算法程序进行介绍：，如果按照层的形式进行读取，也就是从上到下，从左到右，可以进行队列的设计进行读取，这里采用栈的形式进行遍历是从左到右，没有限定从上到下；

5.1.1 中序-递归法

5.1.2 中序-非递归法

5.2 由遍历顺序确定唯一二叉树

  由先序+中序或者后续+中序均能唯一的确定一颗二叉树，其中确定的本质就是利用二叉树的定义是一个递归定义，以及先序是先读取的根，所以由先序可以先确定根，然后再由中序确定左右子树，依次确定即可：

5.2.1 题目练习

5.3 线索二叉树

  就拿中序而讲，一个节点是有五个域，其中分别是：左孩子指针，左孩子标志，节点数据域，右孩子标志位，右孩子指针。线索化二叉树其实就是把树先排序，然后前驱后继就出来了，也就是吧节点的空余指针利用起来，如果左孩子为为空，则指向前驱，如果右孩子为空则指向后继；

5.3.1 遍历线索二叉树

  待补充；遍历顺序由先序线索遍历，中续线索遍历和后续线索遍历。

6 树和森林

  树和森林的遍历，以及森林和二叉树的联系；对于二叉树有四种遍历方式，DLR，LDR，LRD和层次遍历，但是对于树而言，就不同了，这里要注意区别；树只有先根、后根和层次遍历，没有中序，例如5叉树，你一个根有五个节点，那么那个是中间的呢？

6.1 树的存储结构

  有很多存储结构，下面这三种是长常用的；

• 双亲法待补充
• 孩子法待补充
• 孩子兄弟法待补充

6.2 树的遍历

  树的遍历可以类比二叉树的遍历，就是树的遍历少了一种中序遍历；

6.3 森林

  森林是指由零个或多个树组成的一个有序集合,其实其定义还是一个递归的定义，因为好多树，我拿出来一个，剩余的也是森林，再从这个森林里面拿出一个树，剩余的仍然是一个森林。森林可分为三部分：
#pic_center

6.4 深林的遍历

  一般有三种遍历方式，就是先序，中序和后序遍历；
  先序遍历就是对深林中的每颗树都进行先序遍历，从左往右，
  中序遍历就是从左往右依次对深林中的树进行后根遍历（注意与森林和树中，中序的区别）
  森林的中序遍历是指依次对森林中的每棵树进行后根遍历，而森林的后序遍历是指先对森林中的每棵树进行后根遍历，然后再对根结点进行访问

6.5 森林与二叉树的转换

  树的遍历可以类比二叉树的遍历，就是树的遍历少了一种中序遍历；

6.5.1 树与二叉树的转换

  由树转换成二叉树,记住一句口诀：兄弟相连留长子，转45度
  由二叉树转树,记住一句口诀：左孩右-右连双亲，去掉原来右孩线

树和二叉树转换 题目练习

去掉白线就是答案；

6.5.2 森林与二叉树的转换

  由森林转换成二叉树,记住一句口诀：树转二叉根相连
  由二叉树转深林,记住一句口诀：去掉全部右孩线，孤立二叉再还原

森林-二叉树 题目练习

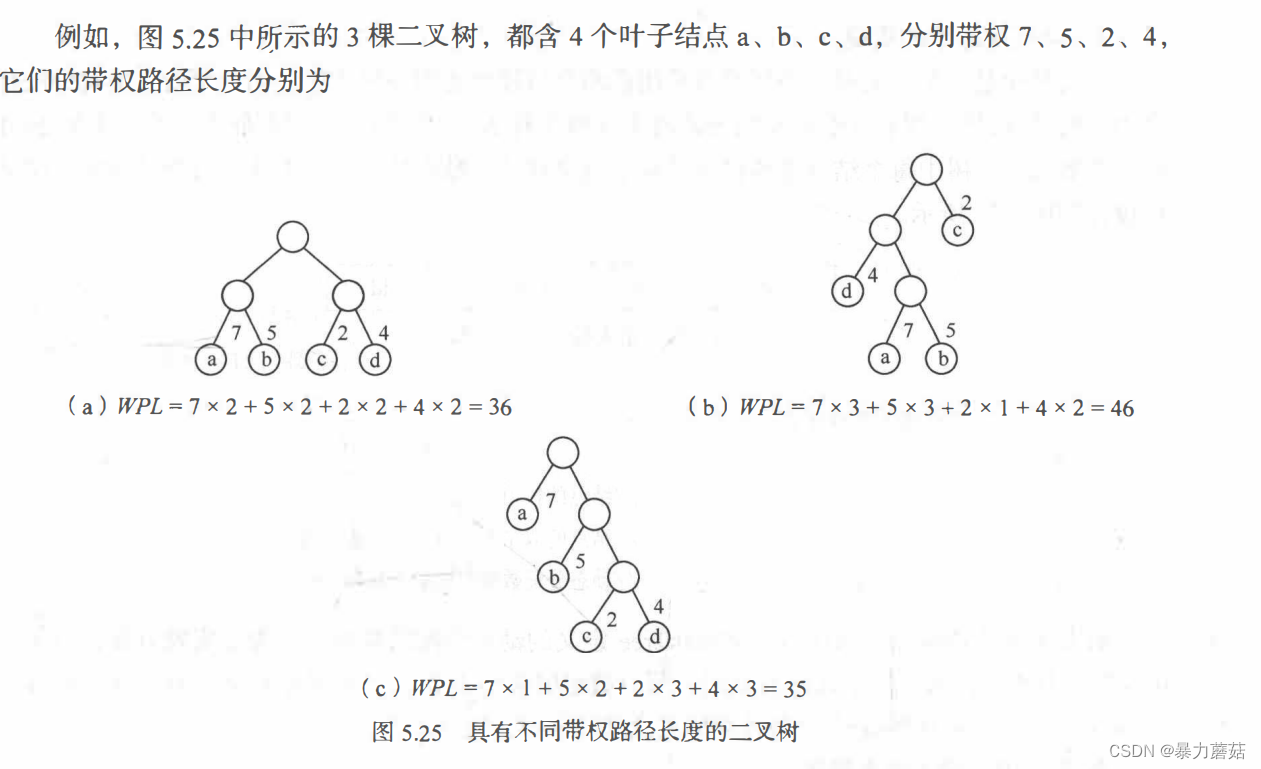
7 哈夫曼树

  哈夫曼树也称为最优树，其基本术语有：哈夫曼树（Huffman Tree）又称最优二叉树，是一种带权路径长度最短的二叉树。

它具有以下几个基本概念：

1. 权值（Weight）：表示每个节点的重要性或出现频率等数值。
2. 带权路径长度（Weighted Path Length）：从树的根节点到某一叶子节点的路径上各节点权值的总和。
3. 构建过程：通过对给定的一组权值进行构造，使得构建出的哈夫曼树的带权路径长度总和最小。
4. 特点：
   • 每个非叶子节点都有两个子节点。
   • 叶子节点代表具体的字符或数据。

哈夫曼树在数据压缩、编码等领域有广泛应用，其主要优点是能有效地减少编码长度，提高数据的存储和传输效率。

实现-构造-编码后续补充