一、问题描述

  给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。
  在「杨辉三角」中，每个数是它左上方和右上方的数的和。
  自我注解：实际上rowIndex是从0开始的

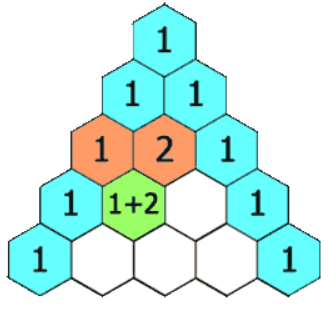
二、示例及约束

示例 1：
输入： rowIndex = 3
输出： [1,3,3,1]

示例 2：
输入： rowIndex = 0
输出： [1]

示例 3：
输入： rowIndex = 1
输出： [1,1]

提示：
● 1 <= numRows <= 33

三、代码

方法一：递推

class Solution {
public:vector<vector<int>> generate(int rowIndex) {vector<vector<int>> ret(rowIndex + 1);//创建二维数组ret，初始数组的行数为numRowsfor (int i = 0; i <= rowIndex; i++) {ret[i].resize(i + 1);//每行初始化为i + 1列ret[i][0] = ret[i][i] = 1;  //每行最左和最右元素固定为1/*每个数是它左上方和右上方的数的和for (int j = 1; j < i; ++j) {ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];}*/for (int j = 1; j <= i / 2; j++) {//对于杨辉三角而言，左右是对称的，因此遍历一半即可ret[i][j] = ret[i - 1][j -1] + ret[i - 1][j];if (i - j != j) {//当i是奇数的时候，最中间的数是加法得到的，不能对称赋值得到ret[i][i - j] = ret[i][j];//对称赋值}}}return ret[rowIndex];}
};//由于对第 i+1 行的计算仅用到了第 i 行的数据，用滚动数组进行优化
class Solution {
public:vector<int> getRow(int rowIndex) {//由于只用到了上一行的数据，因此只需要一维数组存储//pre用来表示上一行的数组，cur用来表示现在这一行的数据vector<int> pre, cur;for (int i = 0; i <= rowIndex; ++i) {cur.resize(i + 1);//初始化数组长度cur[0] = cur[i] = 1;//每一行的起始位置和末尾位置为1for (int j = 1; j < i; ++j) {cur[j] = pre[j - 1] + pre[j];//每个数是它左上方和右上方的数的和}pre = cur;//更新上一行数组信息}return pre;//最后的pre更新后就是cur}
};//继续优化，可以只用一个数组，利用递推式Cn{i}=Cn-1{i} + Cn-1{i-1}
class Solution {
public:vector<int> getRow(int rowIndex) {vector<int> row(rowIndex + 1);//初始化为所需得到的数组长度，默认值为0row[0] = 1;/*对于下面循环的操作，每一行的元素都是基于它之前的行计算得出的。比如要得到第四行的[1,3,3,1]，在此之前第三行是[1,2,1,0]，第二行是[1,1,0,0]，第一行是[1,0,0,0]。这个方法中，只用到了一个数组存储，所以相当于是在上一行的基础上来更新数组，模拟杨辉三角的加法方式。*/for (int i = 1; i <= rowIndex; ++i) {for (int j = i; j > 0; --j) {//从后往前更新row[j] += row[j - 1];//更新值，在自身的值上加前一个值}}return row;}
};

方法二：线性递推

//利用组合数公式Cn{m} = Cn{m-1} * (n-m-1) / m，其中Cn{0} = 1
class Solution {
public:vector<int> getRow(int rowIndex) {vector<int> row(rowIndex + 1);row[0] = 1;for (int i = 1; i <= rowIndex; ++i) {//通过组合数公式，可以得到同一行的相邻组合数的关系row[i] = 1LL * row[i - 1] * (rowIndex - i + 1) / i;/*1LL 是一个整数字面量，它表示一个长整型（long long）的数字 1。使用 1LL 的原因是为了确保在后面的乘法操作中，至少有一个操作数是长整型，从而避免在整数乘法中发生溢出，并确保整个表达式的结果也是长整型，这样整个乘法表达式的结果也将是 long long 类型的，从而能够容纳更大的数值。*/}return row;}
};

四、总结

时间复杂度：
方法一：O($rowInde{x}^2$)。
方法二：O($rowIndex$)。
空间复杂度：
方法一：O(1)，不考虑返回的数组空间。
方法二：O(1)，不考虑返回的数组空间。

方法	时间复杂度	空间复杂度
方法一	O($rowInde{x}^2$)	O(1)
方法二	O($rowIndex$)	O(1)