目录
- 0.原理讲解
- 1.[模板]一维前缀和
- 1.题目链接
- 2.模板代码实现
- 2.[模板]二维前缀和
- 1.题目链接
- 2.算法原理讲解
- 3.模板代码实现
- 3.寻找数组的中心下标
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 4.除自身以外数组的乘积
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
0.原理讲解
-
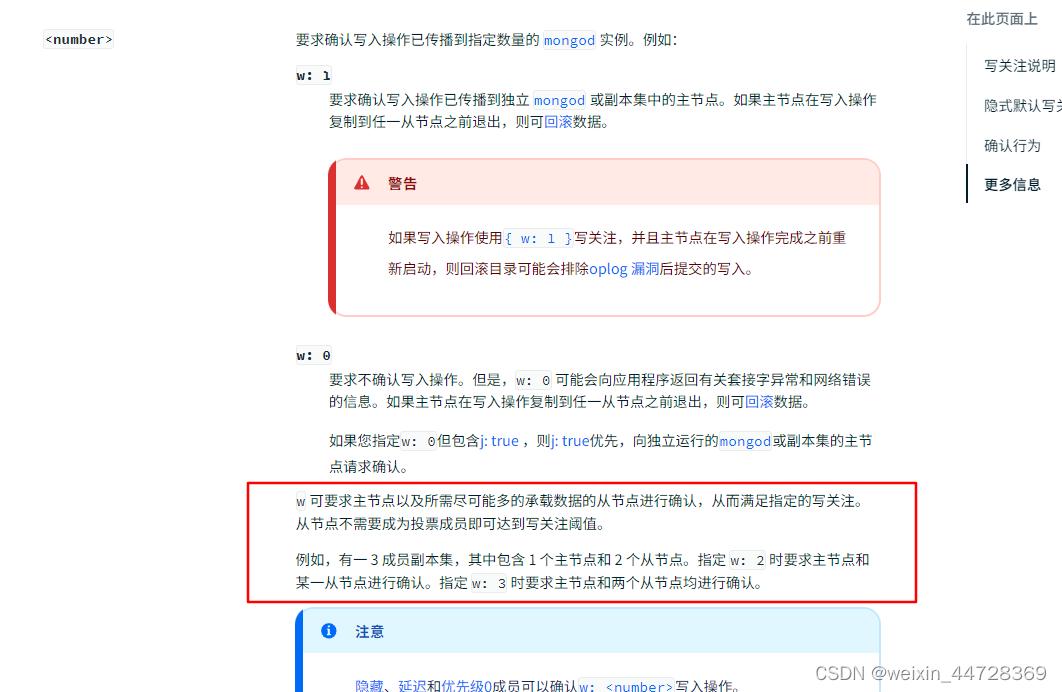
前缀和:快速求出数组中某一个连续区间的和
-
一维前缀和步骤:
-
预处理出来一个前缀和数组
dp[i]表示:[1, i]区间内所有元素的和- 状态方程转移:
dp[i] = dp[i - 1] + arr[i]
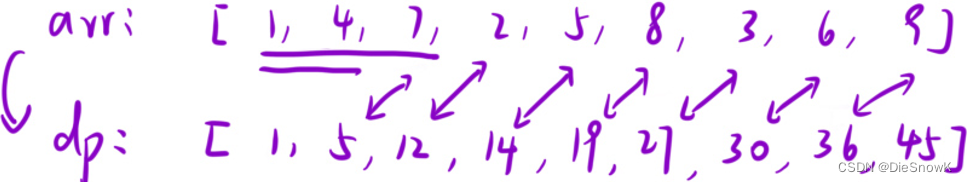
-
使用前缀和数组
[l, r]->dp[r] - dp[l - 1]
-
-
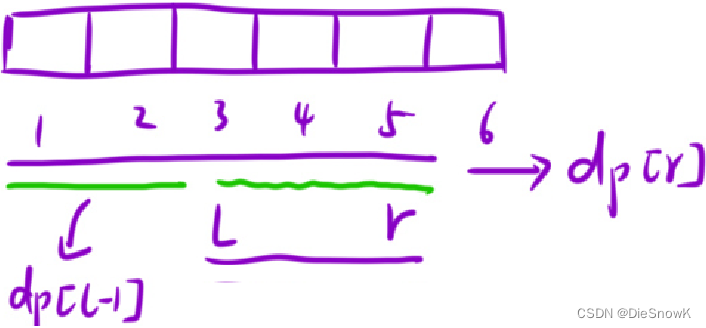
二维前缀和步骤:
-
预处理出来一个前缀和数组
dp[i][j]表示:从[1, 1]位置到[i, j]位置,这段区间里面所有元素的和- 状态方程转移:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1]
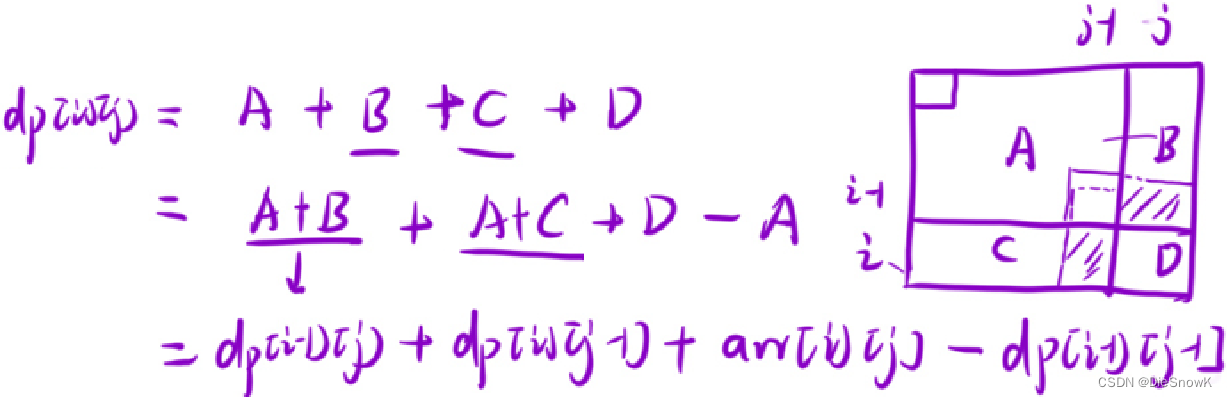
-
使用前缀和数组
- [ x 1 , y 1 ] − [ x 2 , y 2 ] [x_1, y_1] - [x_2, y_2] [x1,y1]−[x2,y2] -> D = d p [ x 2 ] [ y 2 ] − d p [ x 1 − 1 ] [ y 2 ] − d p [ x 2 ] [ y 1 − 1 ] + d p [ x 1 − 1 ] [ y 1 − 1 ] D = dp[x_2][y_2] - dp[x_1 - 1][y_2] - dp[x_2][y_1 - 1] + dp[x_1 - 1][y_1 -1] D=dp[x2][y2]−dp[x1−1][y2]−dp[x2][y1−1]+dp[x1−1][y1−1]
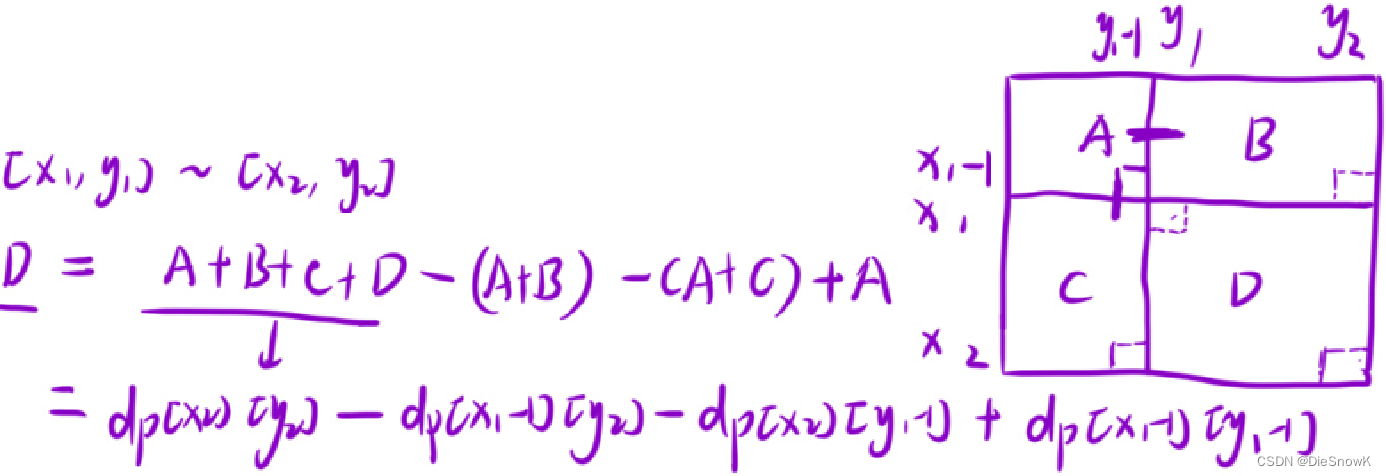
- [ x 1 , y 1 ] − [ x 2 , y 2 ] [x_1, y_1] - [x_2, y_2] [x1,y1]−[x2,y2] -> D = d p [ x 2 ] [ y 2 ] − d p [ x 1 − 1 ] [ y 2 ] − d p [ x 2 ] [ y 1 − 1 ] + d p [ x 1 − 1 ] [ y 1 − 1 ] D = dp[x_2][y_2] - dp[x_1 - 1][y_2] - dp[x_2][y_1 - 1] + dp[x_1 - 1][y_1 -1] D=dp[x2][y2]−dp[x1−1][y2]−dp[x2][y1−1]+dp[x1−1][y1−1]
-
-
为什么下标要从1开始计数?
- 为了处理边界情况
- 倘若
l == 0,那么使用前缀和数组时就会出现dp[r] - dp[-1] - 但此时若从1开始计数,则为
dp[2] - dp[0],此时不会出现任何问题
- 倘若
arr[0] = 0是不会影响其他值的
- 为了处理边界情况
1.[模板]一维前缀和
1.题目链接
- [模板]一维前缀和
2.模板代码实现
int main()
{int n = 0, q = 0;cin >> n >> q;vector<int> arr(n + 1);for(int i = 1; i <= n; i++){cin >> arr[i];}// 预处理出来一个前缀和数组vector<long long> dp(n + 1);for(int i = 1; i <= n; i++){dp[i] = dp[i - 1] + arr[i];}// 使用前缀和数组int l = 0, r = 0;while(q--){cin >> l >> r;cout << dp[r] - dp[l - 1] << endl;}return 0;
}
2.[模板]二维前缀和
1.题目链接
- [模板]二维前缀和
2.算法原理讲解
- 类⽐于⼀维数组的形式,如果能处理出来从
[1, 1]位置到[i, j]位置这⽚区域内所有元素的累加和,就可以在 O ( 1 ) O(1) O(1)的时间内,搞定矩阵内任意区域内所有元素的累加和
3.模板代码实现
int main()
{int n = 0, m = 0, q = 0;cin >> n >> m >> q;// 读取数据vector<vector<int>> arr(n + 1, vector<int>(m + 1));for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cin >> arr[i][j];}}// 预处理前缀和矩阵vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];}}// 使用预处理数组int x1 = 0, y1 = 0, x2 = 0, y2 = 0;long long ret = 0;while(q--){cin >> x1 >> y1 >> x2 >> y2;ret = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];cout << ret << endl;;}return 0;
}
3.寻找数组的中心下标
1.题目链接
- 寻找数组的中心下标
2.算法原理详解
- 由本题可感受出:前缀和类型的题不要硬套模板,题目问什么,根据题目,去微调模板就可以
- 比如
[0, i - 1]中的最大值,也可以用前缀和思想
- 比如
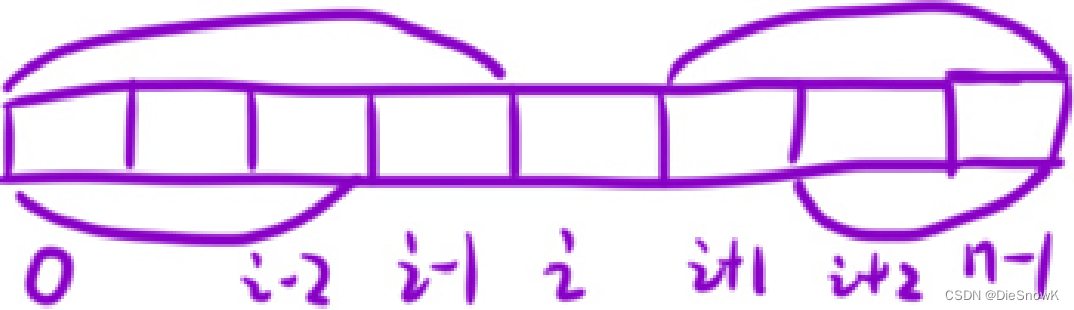
- 从中⼼下标的定义可知,除中⼼下标的元素外,该元素左边的**「前缀和」等于该元素右边的「后缀和」**
- 因此,可以先预处理出来两个数组,⼀个表⽰前缀和,另⼀个表⽰后缀和
- 然后,可以循环枚举可能的中⼼下标,判断每⼀个位置的「前缀和」以及 「后缀和」,如果⼆者相等,就返回当前下标
- 前缀和数组:
f[i]表示:[0, i - 1]区间,所有元素的和- 状态转移方程:
f[i] = f[i - 1] + nums[i - 1]
- 状态转移方程:
- 后缀和数组:
g[i]表示:[i + 1, n - 1]区间,所有元素的和- 状态转移方程:
g[i] = g[i + 1] + nums[i + 1]
- 状态转移方程:
- 细节处理:
f[0] = 0,g[n - 1] = 0f-> 从左向右 /g-> 从右向左
3.代码实现
int PivotIndex(vector<int>& nums)
{int n = nums.size();vector<int> f(n), g(n);// 预处理前缀和数组和后缀和数组// f[i] -> [0, i - 1]区间,所有元素的和for(int i = 1; i < n; i++){f[i] = f[i - 1] + nums[i - 1];}// g[i] -> [i + 1, n - 1]区间,所有元素的和for(int i = n - 2; i >= 0; i--){g[i] = g[i + 1] + nums[i + 1];}// 使用 前缀和 && 后缀和 数组for(int i = 0; i < n; i++){if(f[i] == g[i]){return i;}}return -1;
}
4.除自身以外数组的乘积
1.题目链接
- 除自身以外数组的乘积
2.算法原理详解
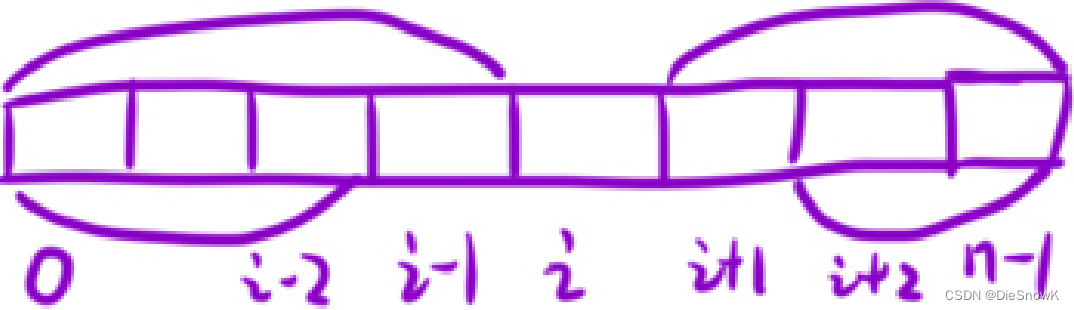
- 前缀积数组:
f[i]表示:[0, i - 1]区间,所有元素的乘积- 状态转移方程:
f[i] = f[i - 1] * nums[i - 1]
- 状态转移方程:
- 后缀积数组:
g[i]表示:[i + 1, n - 1]区间,所有元素的乘积- 状态转移方程:
g[i] = g[i + 1] * nums[i + 1]
- 状态转移方程:
- 细节处理:
f[0] = 1,g[n - 1] = 1`f-> 从左向右 /g-> 从右向左
3.代码实现
vector<int> productExceptSelf(vector<int>& nums)
{int n = nums.size();vector<int> f(n), g(n);f[0] = 1, g[n - 1] = 1; // 细节处理// 预处理前缀积数组和后缀积数组for(int i = 1; i < n; i++){f[i] = f[i - 1] * nums[i - 1];}for(int i = n - 2; i >= 0; i--){g[i] = g[i + 1] * nums[i + 1];}// 使用vector<int> ret(n);for(int i = 0; i < n; i++){ret[i] = f[i] * g[i];}return ret;
}