给你一个链表的头节点 head ，判断链表中是否有环。
    如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
    如果链表中存在环 ，则返回 true 。 否则，返回 false 。

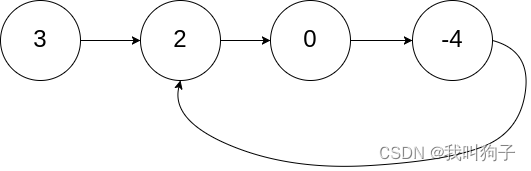
注：图片转载自leetcode官网。

public class Solution {public boolean hasCycle(ListNode head) {ListNode slow = head;ListNode fast = head;if(head == null) return false;while(fast.next != null && fast.next.next != null){slow = slow.next;fast = fast.next.next;if(slow == fast) return true;}return false;}
}

        这题的基本思路是使用快慢指针，快指针每次走两步，慢指针每次走一步，如果链表无环，fast最终会指向null，如果链表有环，则慢指针最终会与快指针相遇。以上图的为示例，说明上述代码的执行过程。slow走一步到2，fast走两步到0，没有相遇。fast走两步到2，slow走一步到0，没有相遇。fast走两步到-4，slow走两步到-4，二者相遇，返回true。

    给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
    如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
    不允许修改链表。

public class Solution {public ListNode detectCycle(ListNode head) {ListNode slow = head;ListNode fast = head;if(head == null) return null;while(fast.next != null && fast.next.next != null){slow = slow.next;fast = fast.next.next;if(fast == slow){slow = head;while(slow != fast){slow = slow.next;fast = fast.next;}return slow;}}return null;}
}

        与上一题相比，这题还需要找到入环的位置。这题的基本思路也是使用快慢指针，快指针每次走两步，慢指针每次走一步，当两个指针相遇时，重新让慢指针从链表头开始走，快指针从相遇点开始走，当两个指针再次相遇的位置即为入环位置。leetcode上给出了详细的解释，这里按个人理解说明一下。

注：图片转载自leetcode官网。
        设链表表头到入环点共有a个结点，指针进入环后按图中顺时针箭头行走，慢指针进入环后走过b个结点后相遇。此时快指针走过的路径为a + n(b + c) + b。b + c为整个环，n表示快指针走过整个环的圈数。同时还需要满足一个要求就是快指针走过的路径是满指针路径的两倍，因为快指针每次走两步，慢指针每次走一步。慢指针走过的路径(结点数)为a + b。快指针走过的路径就为2 * (a + b)，那就是说a + n(b + c) + b = 2 * (a + b)。整理一下得到a = c + (n - 1)(b + c)。也就是说链表头到入环点的路径长等于(n - 1)圈的整个环长度加上相遇点到入环点的距离。换句话说，如果一个指针从链表头出发，一个指针从相遇点出发，那么从链表头开始走的指针走到入环点时，一定会与从入环点开始走的指针相遇，而此时从相遇点开始走的指针走过的路径长度为(n - 1)圈的环长加上相遇点到入环点的距离。这就是为什么快慢指针相遇后，将慢指针(不一定要慢指针，快指针或者重新定义一个指针都可以)从链表头开始走，而快指针从相遇点开始走，当二者再次相遇时，再次相遇点就是入环点。