高级数据结构—线段树（一）-编程知识

学线段树的原因是因为cf的一道题目始终想不出来怎么优化，后来知道区间查询和修改要用到线段树。。。

原题：Iva & Pav

线段树的作用

区间最值查询：可以高效地找到给定区间内的最大值、最小值等。
区间和查询：可以高效地计算给定区间内元素的和、积等。
区间更新：可以高效地对给定区间内的元素进行更新操作，如增加一个固定值、赋值等。
区间覆盖：可以将给定区间内的元素全部赋值为一个固定值。
区间合并：可以将多个区间合并成一个区间，快速地进行区间合并操作。
区间离散化：可以将区间内的元素进行离散化处理，方便进行查询和统计操作。
区间交集：可以快速地找到多个区间之间的交集

线段树和树状数组的区别

刚学完树状数组来学线段树，一开始还不知道他们具体的差别在哪里，那么以下是我的理解。

1.树状数组是前缀和优化，要用到前缀和的时候较为方便。

2.树状数组用来进行单点修改，区间查询；或者区间修改，单点查询较为方便，而区间查询和区间修改较为复杂，因此可以用线段树优化。

3.线段树适用于需要频繁的区间查询和更新操作的问题，如区间最值、区间和等，能够灵活处理各种区间操作。

4.树状数组适用于一维数组的前缀和查询和更新操作，对于简单的区间操作也能够提供高效的解决方案。

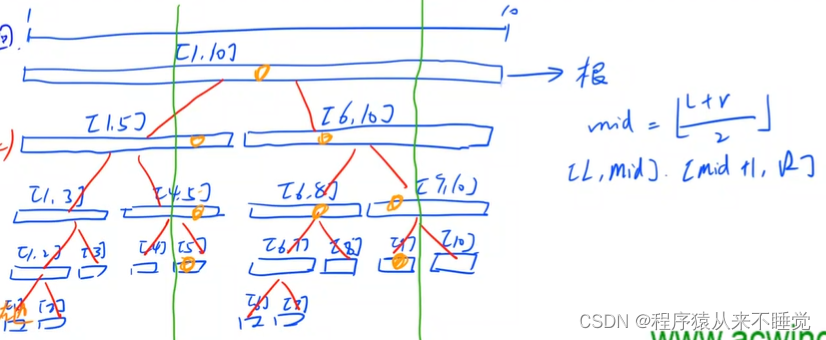
例题：

最大数

题目链接：最大数

直接看代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
//单点插入，区间查询
const int N = 2e5+5;
struct node{int l,r;int v;
}tr[N*4];int m,p;//子节点的信息更新父节点
void pushup(int u){tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
}//u为当前线段树节点编号
void build(int u,int l,int r){tr[u]={l,r};if(l==r)return;int mid=l+r>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);
}//查询以u为根节点，区间[l,r]中的最大值
int query(int u, int l, int r) {//      Tl-----Tr//   L-------------R   //1.不必分治，直接返回if(tr[u].l >= l && tr[u].r <= r) return tr[u].v;int mid = tr[u].l + tr[u].r >> 1;int v = 0;//     Tl----m----Tr//        L-------------R //2.需要在tr的左区间[Tl, m]继续分治if(l <= mid) v = query(u << 1, l, r);//     Tl----m----Tr//   L---------R //3.需要在tr的右区间(m, Tr]继续分治if(r > mid) v = max(v, query(u << 1 | 1, l, r));//     Tl----m----Tr//        L-----R //2.3涵盖了这种情况return v;
}//u为节点编号，x为修改位置，v为修改的值
void modify(int u,int x,int v){if(tr[u].l==tr[u].r)tr[u].v=v;//叶子节点，递归出口else{int mid=tr[u].l+tr[u].r>>1;//分治，修改位置偏左往左边遍历，偏右往右边遍历if(x<=mid)modify(u<<1,x,v);else {modify(u<<1|1,x,v);}pushup(u);//回溯，子节点的信息更新父节点}
}signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);//n表示树中节点个数，last表示上一次查询的结果int n=0,last=0;cin>>m>>p;//初始化线段树，节点的区间最多为[1,m]build(1,1,m);while(m--){char op;cin>>op;if(op=='A'){//添加节点int t;cin>>t;//在n+1处插入modify(1,n+1,(t+last)%p);//节点个数+1n++;}else {int l;cin>>l;//查询[n - L + 1, n]内的最大值，u = 1，即从根节点开始查询last=query(1,n-l+1,n);cout<<last<<"\n";}}return 0;
}

你能回答这些问题吗

题目链接：你能回答这些问题吗

如图：

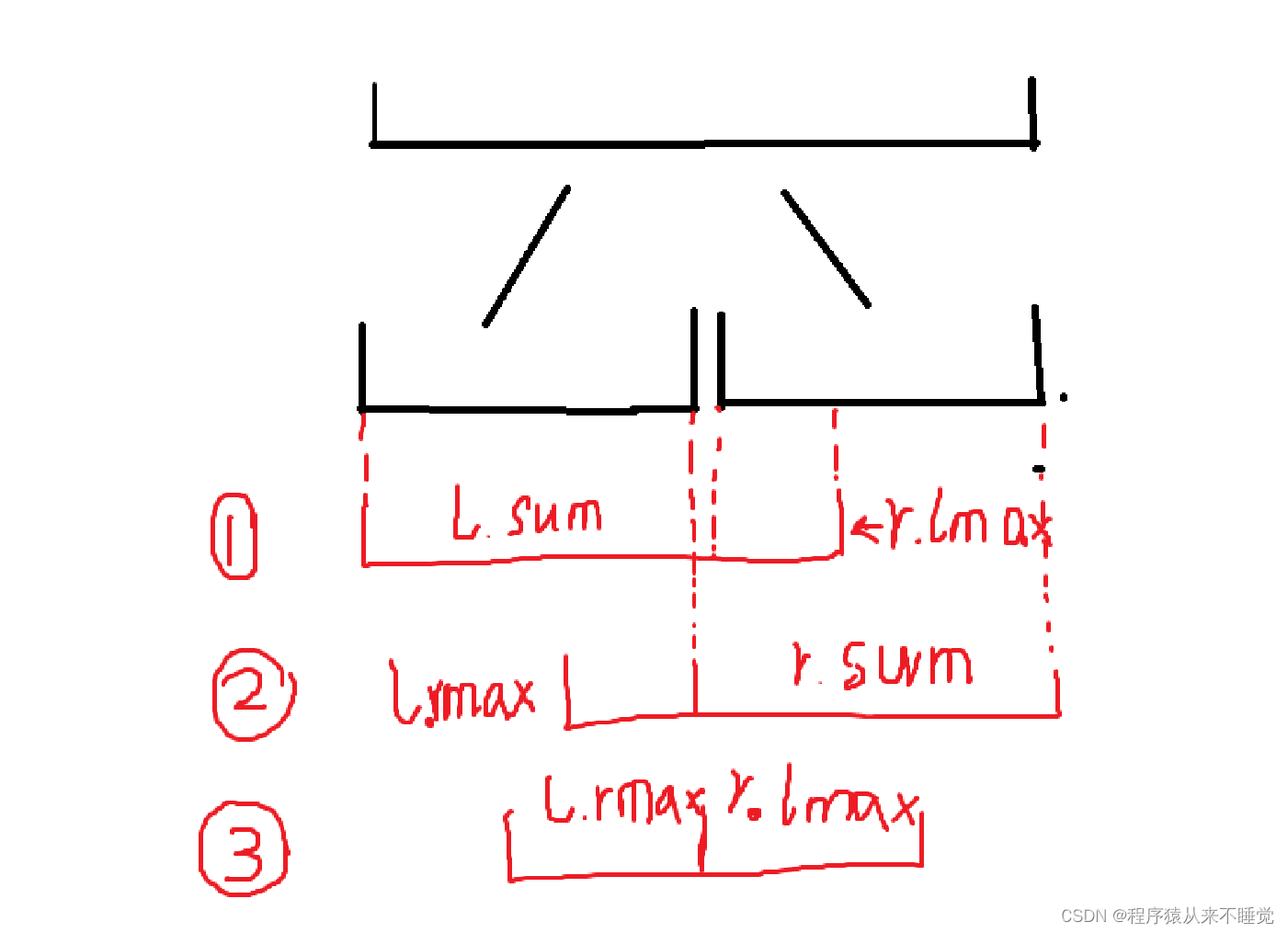
如图，假设我们要求区间的最大子段和，有三种情况：

1.包含所有左半边，部分右半边----->左半边的区间和+右半边的前缀和

2.包含所有右半边，部分左半边----->右半边的区间和+左半边的后缀和

3.中间的一部分----->左半边的后缀和+右半边的前缀和

因此我们的结构体要记录四个信息：

struct node{int l,r;int sum;//[l,r]的区间和int lmax;//最大前缀和int rmax;//最大后缀和int tmax;//区间[l,r]最大连续子段和
}tr[N*4];

同时pushup函数根据上图可以推出：（重载函数）

//u表示该节点，l表示该节点的左子树，r表示该节点的右子树
void pushup(node &u,node &l,node &r){u.sum=l.sum+r.sum;//三种最大连续子段和的情况u.lmax=max(l.lmax,l.sum+r.lmax);u.rmax=max(r.rmax,r.sum+l.rmax);u.tmax=max({l.tmax,r.tmax,l.rmax+r.lmax});
}void pushup(int u){pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}

代码附上：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e5+5;
int w[N];
int n,m;
struct node{int l,r;int sum;//[l,r]的区间和int lmax;//最大前缀和int rmax;//最大后缀和int tmax;//区间[l,r]最大连续子段和
}tr[N*4];//u表示该节点，l表示该节点的左子树，r表示该节点的右子树
void pushup(node &u,node &l,node &r){u.sum=l.sum+r.sum;//三种最大连续子段和的情况u.lmax=max(l.lmax,l.sum+r.lmax);u.rmax=max(r.rmax,r.sum+l.rmax);u.tmax=max({l.tmax,r.tmax,l.rmax+r.lmax});
}void pushup(int u){pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}void build(int u,int l,int r){if(l==r)tr[u]={l,r,w[r],w[r],w[r],w[r]};//找到叶子节点else{tr[u]={l,r};//设当前区间为[l,r]int mid=l+r>>1;build(u<<1,l,mid);//左子树build(u<<1|1,mid+1,r);//右子树pushup(u);//修改父节点}
}//每次从1号节点开始找，找到位置位于x的数，并把它修改为v
void modify(int u,int x,int v){if(tr[u].l==x && tr[u].r==x)tr[u]={x,x,v,v,v,v};else{int mid=tr[u].l+tr[u].r>>1;if(x<=mid)modify(u<<1,x,v);//x位于当前区间的左半子区间else modify(u<<1|1,x,v);//x位于当前区间的右半子区间pushup(u);//修改父节点的相关信息}
}node query(int u,int l,int r){if(tr[u].l>=l&&tr[u].r<=r)return tr[u];//被包含else{int mid=tr[u].l+tr[u].r>>1;if(r<=mid)return query(u<<1,l,r);//查询左半区间else if(l>mid)return query(u<<1|1,l,r);//查询右半区间else{//横跨左右区间auto left=query(u<<1,l,r);auto right=query(u<<1|1,l,r);node res;pushup(res,left,right);return res;}}
}signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++)cin>>w[i];build(1,1,n);//建树int k,x,y;while(m--){cin>>k>>x>>y;if(k==1){//查询if(x>y)swap(x,y);cout<<query(1,x,y).tmax<<"\n";}else modify(1,x,y);//修改}return 0;
}