一、固定长度的情况:
最小和(sum)
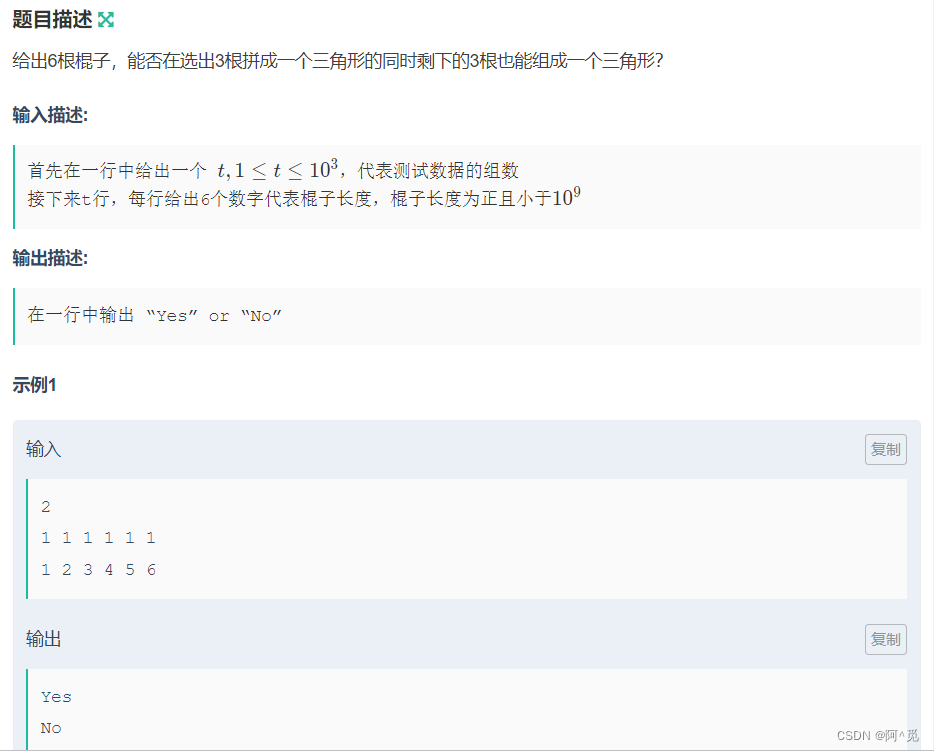
输入N个数的数列,所有相邻的M个数的和共有N-M+1个,求其中的最小值。
输入格式
第1行,2个整数N,M,范围在[3…100000],N>M。
第2行,有N个正整数,范围在[1…1000]。
输出格式
1个数,表示最小和。
输入/输出例子1
输入:
6 3
10 4 1 5 5 2
输出:
10
【方法一】:枚举开始点,计算连续M个数的和,求出最小值。
程序如下:
#include<bits/stdc++.h>
using namespace std;
long long n,m,a[100005],mins=0x7f7f7f7f7f7f7f7f;
int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n-m+1;i++){long long s=a[i];for(int j=i+1;j<=i+m-1;j++)s+=a[j];mins=min(s,mins);}cout<<mins;return 0;
}时间复杂度是o(n*m)如果数据量太大会超时。
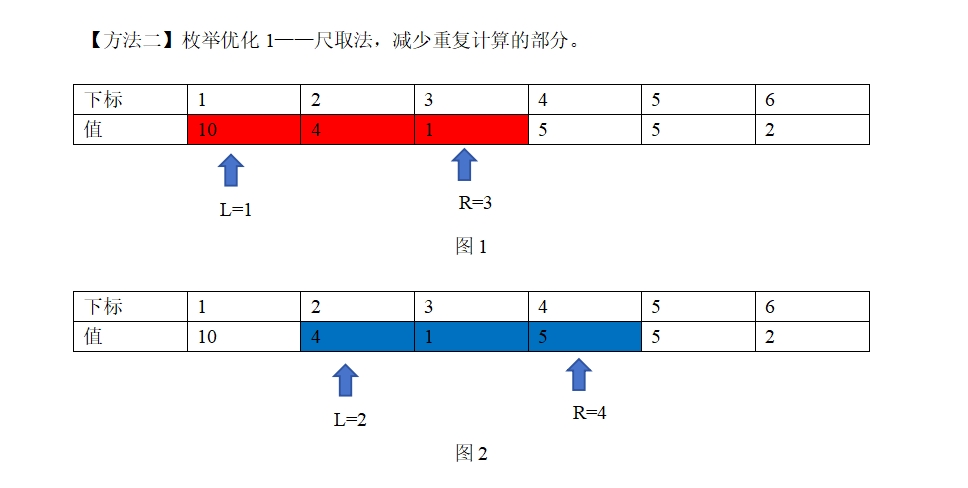
如图1所示,如果以第一个数开始计算也就是图1红色部分。
s1=a[1]+a[2]+a[3]
如图2所示,如果以第二个数开始计算也就是图2蓝色部分
s2=a[2]+a[3]+a[4]
对比图1和图2,公式s1和s2,我们会发现,如果以第一个数开始枚举m=3个数的和,和以第二个数开始枚举m个数的和,重复了a[2]+a[3],也就是说,我们第一个数开始枚举完m个数的和后,完全不用从第二个数再重新枚举,只要在s1的基础上保留重复部分a[2]+a[3],去掉左边的a[1],加入右边的a[4],让长度保持m个。
s1=a[1]+a[2]+a[3]
s2=s1-a[1]+a[4]
尺取法:就如尺子一样,利用两个指针L和R,L代表左边枚举开始点,,R代表枚举结束点,s代表区间L到R的和,如果此时L到R刚好m个数,也就是R-L+1==m,那么找到一个长度为m的和,后面只要把s=s-a[L]+a[R+1],L++,R++,让其长度保持为m。
【程序如下】:
#include<bits/stdc++.h>
using namespace std;
long long n,m,s,a[100005],mins=0x7f7f7f7f7f7f7f7f;
int main(){cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];for(int L=1,R=1;R<=n;R++){s+=a[R];if(R-L+1==m){mins=min(mins,s);s=s-a[L];L++;}}cout<<mins;return 0;
}二、不固定长度情况
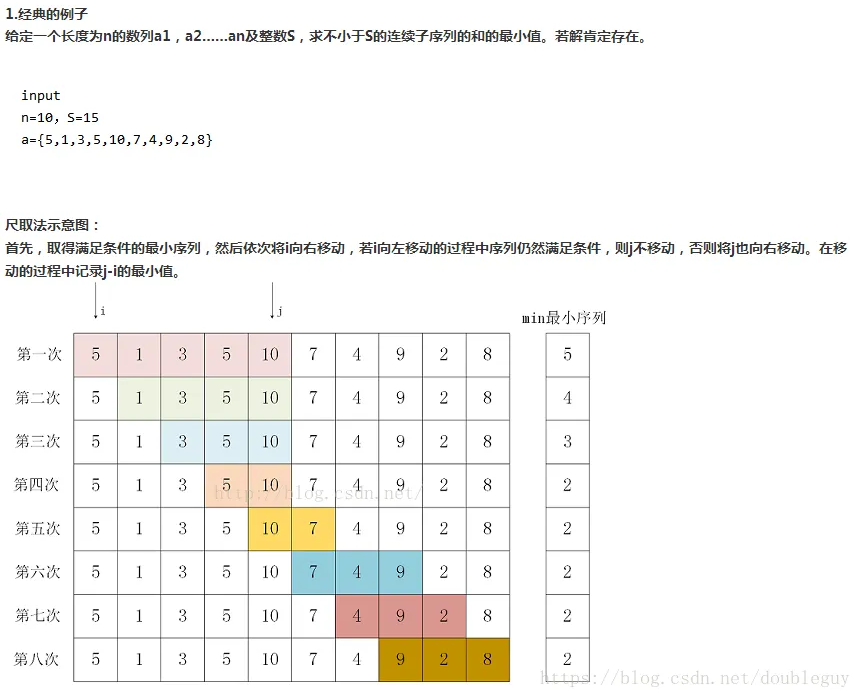
【程序如下】:
#include<bits/stdc++.h>
using namespace std;
long long n,m,s,a[100005];
int main(){cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];int minL=n+1;for(int L=1,R=1;R<=n;R++){s+=a[R];while(s>=m){minL=min(minL,R-L+1);s=s-a[L];L++;}}cout<<minL;return 0;
}三、总结
尺取法是一种线性算法,也是一种高效的枚举区间的方法。
记 (l,r)两个端点为一个序列内以l为起点的最短合法区间,如果r随l的增大而增大的话,我们就可以使用尺取法。
具体的做法是:
1.初始化左右端点
2.不断扩大右端点,直到满足条件
3.如果第二步中无法满足条件,则终止,否则更新结果
4.将左端点扩大1,然后回到第二步
因为r随 l增大而增大,所以 r只有 n次变化的机会,所以时间复杂度为O(n)。