可验证且无经销商
分布式密钥生成 (DKG) 是一种加密协议,使多方能够协作生成共享密钥,而无需任何一方完全了解密钥。 它通过在多个参与者之间分配信任来增强各种应用程序的安全性,从而降低密钥泄露的风险。 我们引入了一种可验证且无经销商的 DKG,适合在区块链中使用。
Shamir 密钥共享(SSS)
Shamir的密钥共享 (SSS) 是一种密码学方法,允许将密钥分为多个部分,每个参与者都持有一部分密钥,称为共享。 SSS 的关键特征是,只有当预定义数量的共享(称为阈值)组合在一起时才能重建密钥。 它是一个阈值方案,表示为 (t,n),其中 n 是分配的份额总数,t 是重构密钥所需的最小份额数量。
SSS 方案的核心是点唯一定义多项式的数学概念。 具体来说,需要两个点来定义直线,需要三个点来定义抛物线,等等。 因此,次数为 (t-1) 的多项式由 t 个点唯一确定。 在此方案中,构建了一个 (t-1) 次多项式,使得 n 个参与者中的每一个都与该多项式上的一个点相关联,该点编码了一个密钥。 为了恢复多项式,从而恢复密钥,只需要这些点中的 t 个。 任何由 t 个参与者组成的组,每个人都持有自己的份额,都可以重建原始的次数多项式 (t-1)。 该密钥作为 y 截距嵌入到多项式中,表示多项式在 x=0 处的值,这实际上使其成为多项式的常数项。 通过这种方法,可以安全、准确地检索密钥。
让我们检查 (3, 4) 密钥共享方案。 负责划分密钥的实体(称为经销商)构造一个 2 次多项式,即 (t-1):
f(x) = s + a₁x + a₂x²
s 表示 y 轴截距处的密钥值(即 f(0)),而 a₁ 和 a2 是随机数。
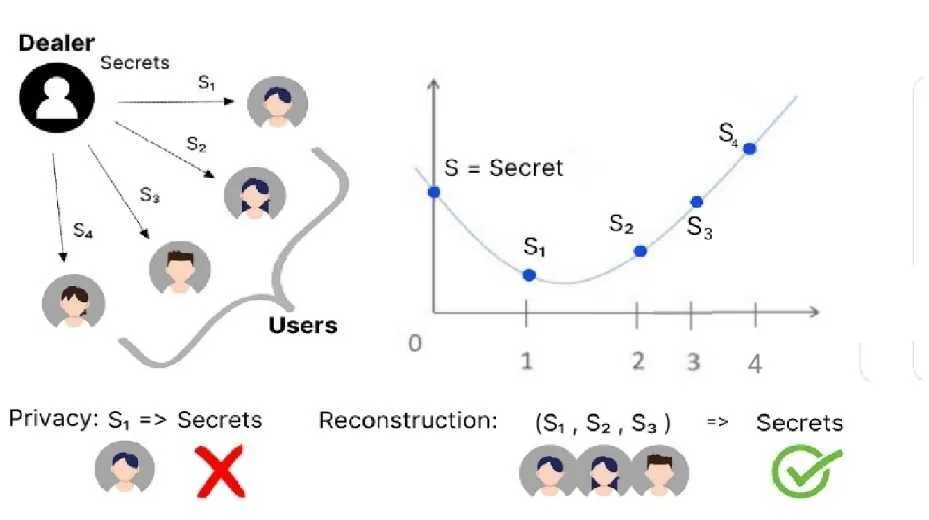
SSS 由两个主要过程组成:
- 密钥份额的分配:在分配阶段,交易者将密钥分成几个部分或份额,并将其分配给一组
n(即 4)个参与者。 每个参与者Pᵢ都会收到一份份额sᵢ = f(i)。 - 密钥的重建:重建过程仅允许
t(即 3)个参与者组合他们的份额并恢复原始密钥,而少于t份的任何其他组都无法推断出有关该密钥的任何重要信息。 例如,前3个参与者可以形成一组点(1, s₁)、(2, s2)和(3, s₃)并重建唯一的多项式f(x),通常使用拉格朗日插值方法。 密钥s就是f(0)。
Youtube 上密钥共享的可视化解释
可验证的密钥共享(VSS)
在Shamir密钥共享中,参与者不知道自己收到的份额与其他参与者收到的份额是否一致。 例如,恶意经销商给予 P₁、P2 和 P₃ 正确的份额 f(1)、f(2) 和 f(3),但给予 P₄ 错误的份额,即不是 f(4)。 如果稍后选择 P₄,则无法正确恢复密钥值。
可验证密钥共享(VSS)是 Shamir 密钥共享方案的扩展,允许验证密钥共享的正确性。 这是在不泄露共享本身的情况下完成的,否则每个人都知道所有共享,从而可以恢复密钥本身,从而破坏了密钥共享的整个目的。
在 VSS 中,除了份额之外,经销商还向每个参与者发送对所有多项式系数的承诺。 一种提交方法是使用椭圆曲线:
c₀ = sGc₁ = a₁Gc₂ = a₂G
cᵢ 承诺 aᵢ。 G 是生成点。
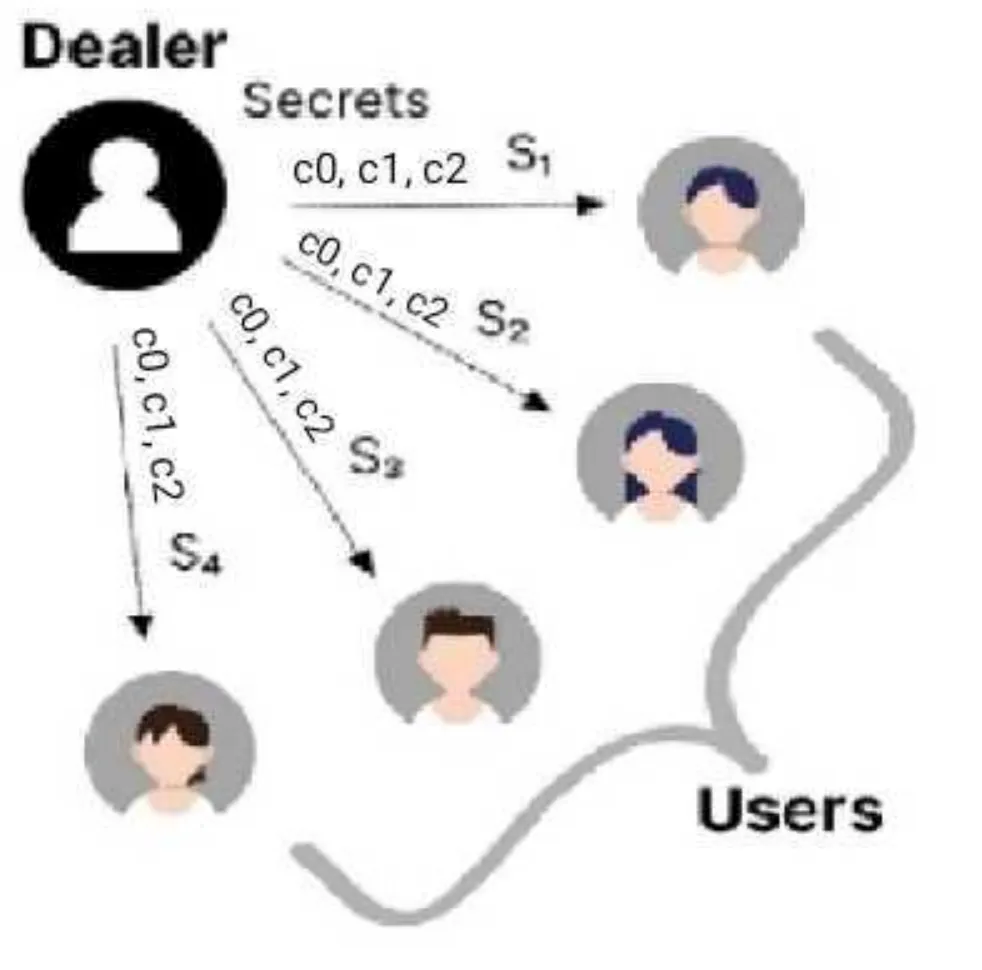
Pᵢ 可以通过检查以下等式是否成立来独立验证其份额的有效性:
f(i)G =? c₀ + c₁i + c₂i²
这是因为:
f(i)G = (s + a₁i + a₂i²)G = sG + a₁iG + a₂i²G = c₀ + c₁i + c₂i²
请注意,她知道方程式中所需的所有信息。 如果等式不成立,她就知道经销商不诚实,可以直接终止。
分布式密钥生成
在这个阶段,我们已经掌握了分发密钥的技术,以便所有参与者都可以接收并验证它。 然而,我们面临着一个问题——经销商知道最初的密钥。
分布式密钥生成(DKG)通过允许每个参与者为密钥的整体随机性做出贡献来解决这个问题。 无经销商 DKG 基本上进行 n 次独立的 VSS 运行。 在第 i 次运行中,Pᵢ 充当经销商来分发密钥 sᵢ。 每个参与者从其他参与者那里收集密钥份额,最终份额是每次运行中份额的总和。 最终的密钥是所有运行中密钥的总和。
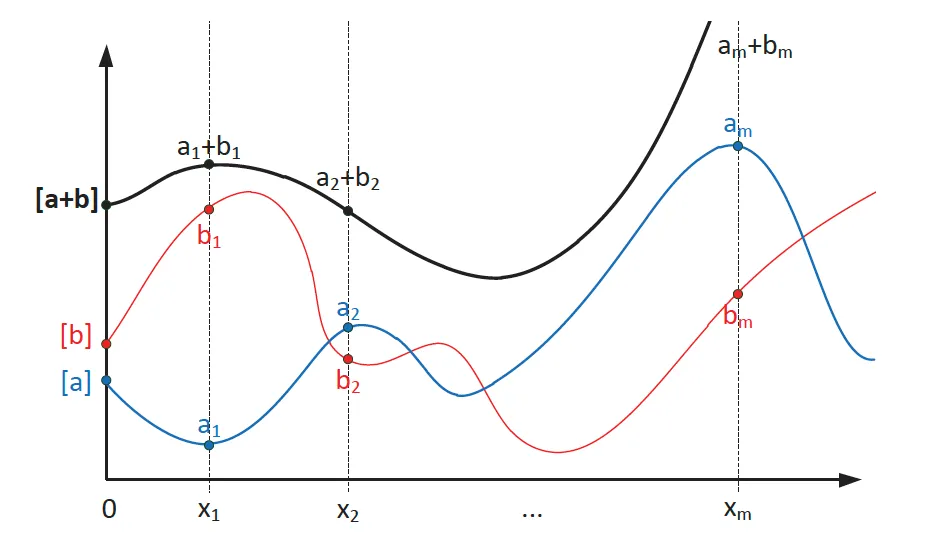
为了了解原因,让我们考虑以下两个代表密钥 a 和 b 的多项式:
f₁(x) = a + a₁x + a₂x² + …f₂(x) = b + b₁x + b₂x² + …
这两个多项式可以相加形成最终的密钥多项式:
f(x) = (a+b) + (a₁+b₁)x + (a₂+b₂)x² + …
f(x) 编码密钥 a+b,它是两个单独密钥的总和。 它的份额也是原始两个多项式的两个单独份额的总和。






![[Java EE] 多线程(五):单例模式与阻塞队列](https://img-blog.csdnimg.cn/direct/f0735e2549b642828382bde20623bbca.png)