【算法基础实验】图论-深度优先搜索和深度优先路径-编程知识

深度优先(DFS)

理论基础

深度优先搜索（DFS, Depth-First Search）是图和树的遍历算法中的一种，它从一个节点开始，沿着树的边走到尽可能深的分支，直到节点没有子节点为止，然后回溯继续搜索下一个分支。DFS 是一种使用递归或栈实现的算法，它深入到每一个分支直到无路可走再退回到上一个分岔点，这种方式有助于解决许多搜索和路径问题。

DFS 的基本步骤

标记和访问：从一个未访问的节点开始，标记它为已访问。
递归探索：对于当前节点的每一个未访问的相邻节点，继续执行深度优先搜索（递归调用DFS）。
回溯：当一个节点的所有相邻节点都被访问后，回溯到之前的节点继续探索未访问的节点。

DFS 的特点

深度优先：它尝试尽可能深地搜索图的分支。
使用栈：无论是显式使用栈还是通过递归调用的隐式栈，DFS 都利用栈先进后出的特性来管理节点和回溯。
可能非最短路径：DFS 不保证找到的是最短路径，它可能在找到目标前遍历图中大部分节点。
解空间树：在涉及路径和状态的问题中，DFS 常用于生成解空间树，并通过回溯剪枝。
复杂性：在最坏的情况下，DFS 的时间复杂度是 O(V+E)，其中 V 是顶点数，E 是边数。

DFS 的应用场景

路径搜索：在迷宫或图中查找从起点到终点的路径。
拓扑排序：在有向无环图中进行拓扑排序。
连通分量：在无向图中查找所有连通分量。
解决问题：如解决迷宫问题、路径问题和那些可以通过回溯方法解决的问题。

简单总结

深度优先搜索是一个递归的过程，它尝试深入到每一个分支直到不能再深入为止，然后通过回溯继续探索其他分支。它的核心在于尝试所有可能的路径直到找到解决方案或覆盖所有的节点。DFS 的记忆点在于它的递归性质和回溯机制，这使得它非常适合处理需要探索所有可能性的问题。

前提

JAVA实验环境

实现Bag抽象数据结构

实现Stack抽象数据结构

实现无向图的构建

数据结构

本算发中涉及到的基本数据结构

private boolean[] marked
private int[] edgeTo
private final int s
myLinkedStack //一种栈的实现，具体见以下链接
myGraph //一种无向图的实现

myGraph的数据结构图

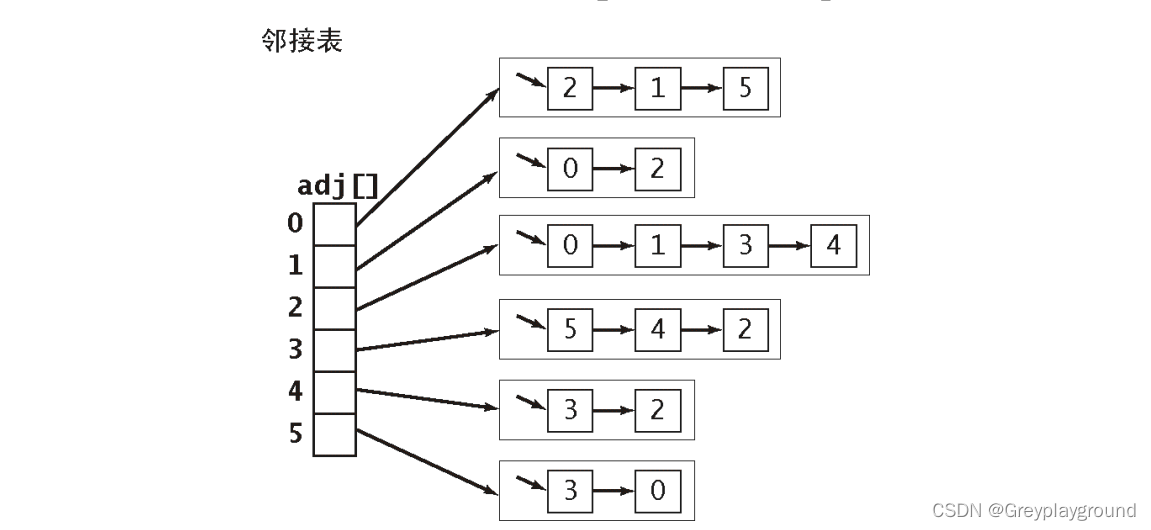
请添加图片描述

实验数据和实验环境

本实验要求根据DFS算法实现从任意一点的深度优先路径的打印功能

实验数据是一个名为tinyCG.txt的文件，用来构建如下图所示的无向图

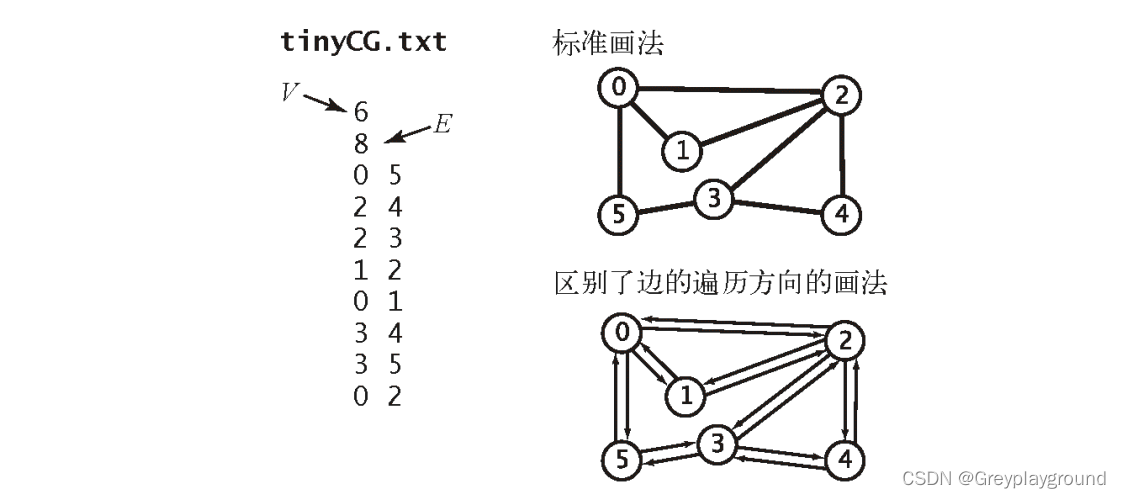
请添加图片描述

算法流程

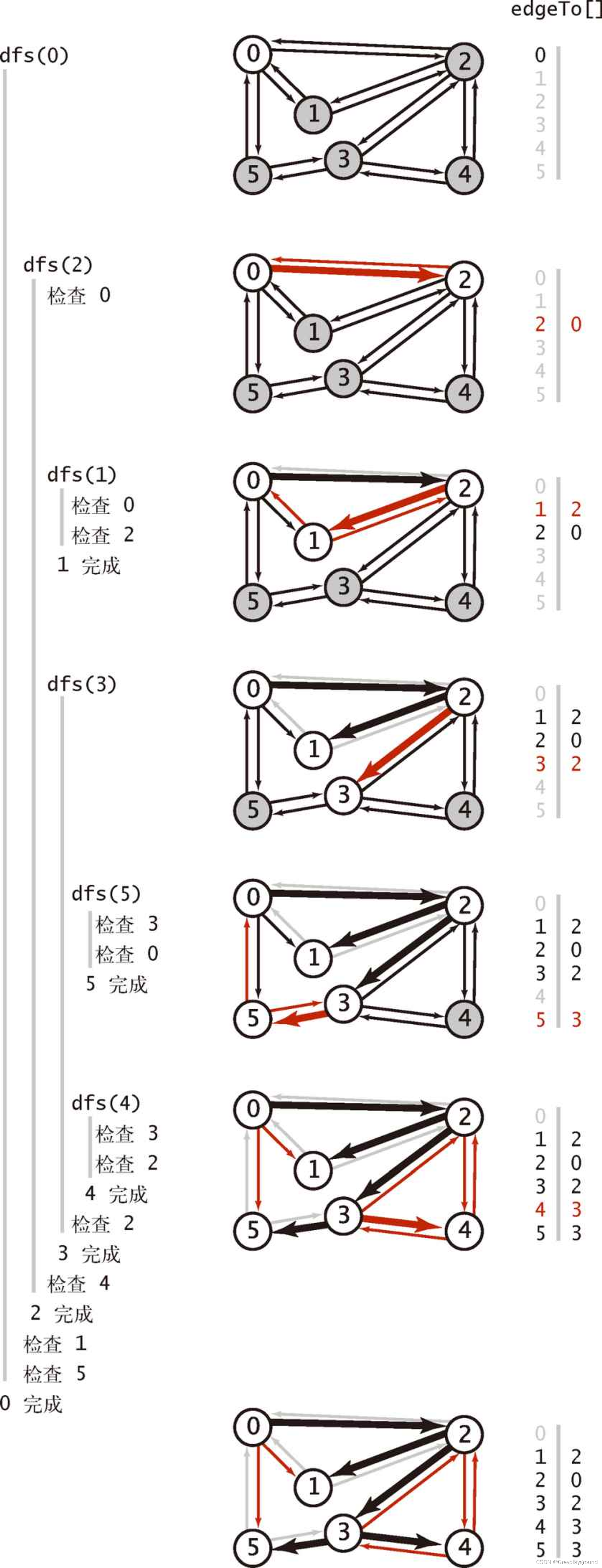
请添加图片描述

根据以上深度优先搜索得到的结果，整理输出从起点到图中所有点的

下图为从0到5的深度优先路劲的计算过程，我们可以计算出从任意起点到其他所有点的深度优先路径

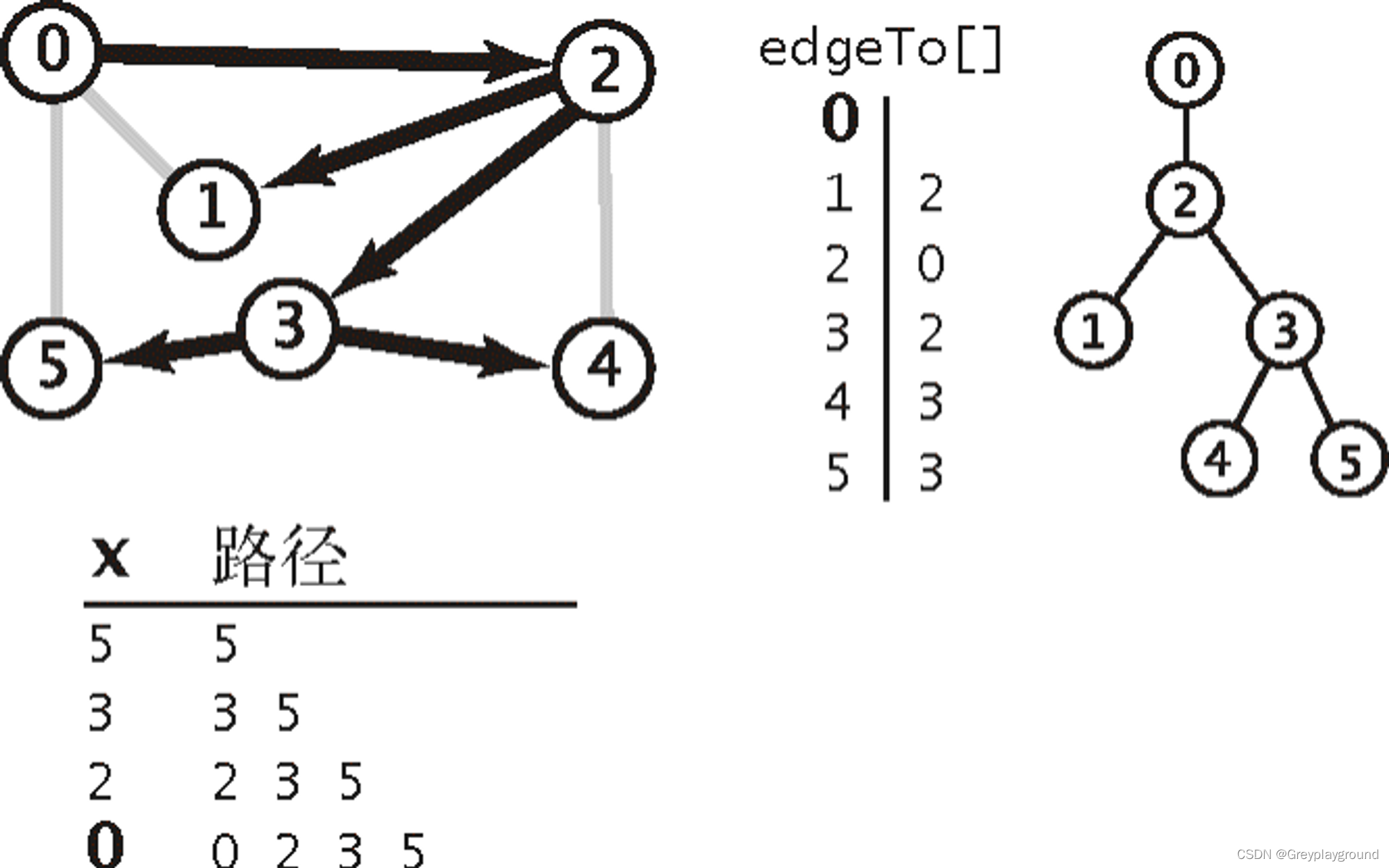
请添加图片描述

代码实现

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;public class myDepthFirstPaths {private boolean[] marked;private int[] edgeTo;private final int s;public myDepthFirstPaths(myGraph G, int s){this.s = s;marked = new boolean[G.V()];edgeTo = new int[G.V()];dfs(G, s);}private void dfs(myGraph G, int v){marked[v] = true;for(int w:G.adj(v))if(!marked[w]){edgeTo[w]=v;dfs(G,w);}}public boolean hasPathTo(int v){return marked[v];}public Iterable<Integer> pathTo(int v){if(!hasPathTo(v)) return null;myLinkedStack<Integer> path = new myLinkedStack<Integer>();for(int x=v;x!=s;x=edgeTo[x]) path.push(x);path.push(s);return path;}public static void main(String[] args){myGraph G = new myGraph(new In(args[0]));int s = Integer.parseInt(args[1]);myDepthFirstPaths search = new myDepthFirstPaths(G,s);for(int v=0; v < G.V(); v++){StdOut.print(s+" to "+v+":");if(search.hasPathTo(v)){for(int x:search.pathTo(v))if(x==s) StdOut.print(x);else StdOut.print("-"+x);StdOut.println();}}}
}

代码详解

这段代码实现了一个用于无向图的深度优先搜索（DFS）路径查找类 myDepthFirstPaths。它可以找到从一个给定的起始顶点 s 到图中任意其他顶点的路径。以下是代码的详细解读和功能介绍：

类定义与变量


public class myDepthFirstPaths {private boolean[] marked;  // 用于标记每个顶点是否已被访问private int[] edgeTo;      // 从起点到一个顶点的已知路径上的最后一个顶点private final int s;       // 起始顶点

marked[] 数组用于跟踪每个顶点是否被访问过。
edgeTo[] 数组记录到达每个顶点的最后一步的前一个顶点。
s 是算法开始的起点。

构造函数


public myDepthFirstPaths(myGraph G, int s){this.s = s;marked = new boolean[G.V()];edgeTo = new int[G.V()];dfs(G, s);
}

构造函数初始化 marked 和 edgeTo 数组，并从顶点 s 开始对图 G 进行深度优先搜索。

深度优先搜索方法


private void dfs(myGraph G, int v){marked[v] = true;for(int w: G.adj(v))if(!marked[w]){edgeTo[w] = v;dfs(G, w);}
}

这是一个递归方法，它标记顶点 v 为已访问，然后对于每个与 v 相邻的未访问顶点 w，记录 w 是从 v 达到的，并递归地继续深度优先搜索。

路径检查与生成


public boolean hasPathTo(int v){return marked[v];
}public Iterable<Integer> pathTo(int v){if (!hasPathTo(v)) return null;myLinkedStack<Integer> path = new myLinkedStack<Integer>();for (int x = v; x != s; x = edgeTo[x])path.push(x);path.push(s);return path;
}

hasPathTo 方法检查是否存在从起点 s 到顶点 v 的路径。
pathTo 方法返回从起点 s 到顶点 v 的路径，使用一个自定义的栈 myLinkedStack 来逆序存储路径。

主方法


public static void main(String[] args){myGraph G = new myGraph(new In(args[0]));int s = Integer.parseInt(args[1]);myDepthFirstPaths search = new myDepthFirstPaths(G, s);for (int v = 0; v < G.V(); v++){StdOut.print(s + " to " + v + ":");if (search.hasPathTo(v)){for (int x : search.pathTo(v))if (x == s) StdOut.print(x);else StdOut.print("-" + x);}StdOut.println();}
}

主方法从文件中读取图，并从指定的起点 s 开始搜索。对于图中的每个顶点 v，如果存在从 s 到 v 的路径，则打印该路径。

这个程序展示了如何使用深度优先搜索来找出图中从一个特定起点到所有其他顶点的路径。这些路径可以用于多种应用，比如网络路由、社交网络中的连接查找等。

实验

编译代码

javac myDepthFirstPaths.java

运行代码

代码运行要输入两个参数，首先是用于构造无向图的tinyCG.txt文件，第二个是起点的数值

最终的打印结果是从0分别到1,2,3,4,5的深度优先路径

java myDepthFirstPaths tinyCG.txt 0 
0 to 0:0
0 to 1:0-2-1
0 to 2:0-2
0 to 3:0-2-3
0 to 4:0-2-3-4
0 to 5:0-2-3-5

参考资料

算法（第4版）人民邮电出版社