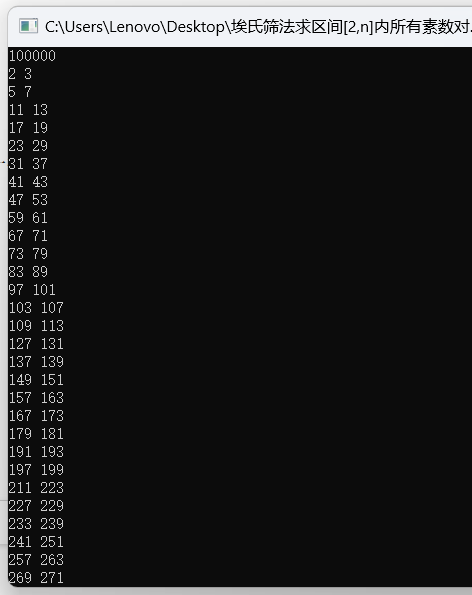
1.埃式筛法:求区间[2, n]内所有的素数对
【参考代码】
#include <bits/stdc++.h>
using namespace std;const int N = 1e5;
vector<int> prime;
bool visit[N];int main()
{int n;cin>>n;memset(visit, false, sizeof(visit));for(int i=2; i<=sqrt(n); i++){if(visit[i] != true) //i是素数{for(int j=i*i; j<=n; j += i) //原来是2i。优化后i*i。i=5时,2*5 3*5 4*5已经在前面i=2,3,4筛过了{visit[j] = true; //i*2,3,4,5...都不是素数}}}//通过visit数组记录素数for(int i=2; i<=n; i++){if(visit[i] != true) //i是素数{prime.push_back(i);}}for(int i=0; i<prime.size(); i+=2){cout << prime[i] << ' ' << prime[i+1] << endl;}return 0;
}【测试结果】
2.求第一亿个Fibonacci数
【参考代码】
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1000000007;struct matrix{ll a[2][2];
};matrix start;
matrix result;//(Fn+1) = (1, 1)^n * (F1)
//(Fn ) (1, 0) (F0)//矩阵乘法
matrix matrix_multiplication(matrix matrix1, matrix matrix2)
{matrix temporary;temporary.a[0][0] = (matrix1.a[0][0] * matrix2.a[0][0] + matrix1.a[1][0] * matrix2.a[0][1]) % mod;temporary.a[0][1] = (matrix1.a[0][0] * matrix2.a[0][1] + matrix1.a[0][1] * matrix2.a[1][1]) % mod;temporary.a[1][0] = (matrix1.a[0][0] * matrix2.a[1][0] + matrix1.a[0][1] * matrix2.a[1][1]) % mod;temporary.a[1][1] = (matrix1.a[1][0] * matrix2.a[0][1] + matrix1.a[1][1] * matrix2.a[1][1]) % mod;return temporary;
}//矩阵快速幂
void fastpow(int n)
{while(n){if(n & 1) //位运算,最后一位是否为1result = matrix_multiplication(start, result);start = matrix_multiplication(start, start);n = n >> 1; //右移一位}
}int main() //计算第1亿个Fibonacci数
{int n = 1e8; //一亿start.a[0][0] = start.a[0][1] = start.a[1][0] = 1, start.a[1][1] = 0;//(1, 0)//(0, 1)result.a[0][0] = result.a[1][1] = 1, result.a[1][0] = result.a[0][1] = 0;fastpow(n);
// cout << result.a[0][0] % mod << endl;
// cout << result.a[0][1] % mod << endl;cout << result.a[1][0] % mod << endl;
// cout << result.a[1][1] % mod << endl;return 0;
}
//100000000
//908460138【输出结果】
由于答案是一个极大的数,我们取最后9位输出
908460138