给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
前序遍历的首元素 为 树的根节点 node 的值

在中序遍历中搜索根节点 node 的索引 ,可将 中序遍历 划分为 [ 左子树 | 根节点 | 右子树 ]

根据中序遍历中的左(右)子树的节点数量,可将 前序遍历 划分为 [ 根节点 | 左子树 | 右子树 ]

根节点在前序遍历的索引 root 、左子树在中序遍历的左边界 、右子树在中序遍历的右边界
当 left > right ,代表已经越过叶节点,此时返回 null
递推工作:
建立根节点 node : 节点值为 preorder[root]
划分左右子树: 查找根节点在中序遍历 inorder 中的索引 i
构建左右子树: 开启左右子树递归
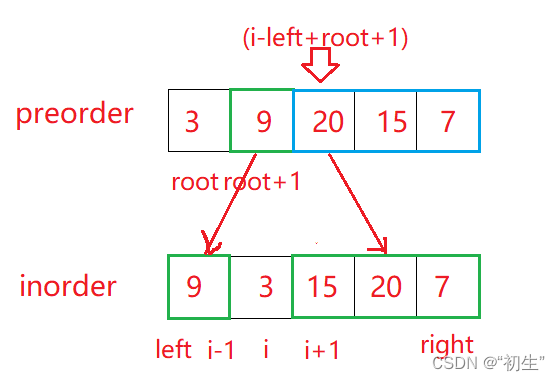
如上图可得规律
| 根节点索引 | 中序遍历左边界 | 中序遍历右边界 | |
|---|---|---|---|
| 左子树 | root + 1 | left | i - 1 |
| 右子树 | i - left + root + 1 | i + 1 | right |
为了快速找到前序遍历元素在中序遍历中下标,采取哈希来记录
完整代码如下
class Solution{
private:vector<int> preorder;unordered_map<int, int> indexMap;ThreeNode*dfs(int root,int left,int right){if(left>right) return nullptr;ThreeNode*root = new ThreeNode(preorder[root]);int i = indexMap[preorder[root]];root->left = dfs(root+1,left,i-1);root->right = dfs(i-left+root+1,i+1,right);return root;}
public:ThreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = preorder.size();this->preorder = preorder;for(int i=0;i<n;i++){indexMap[inorder[i]] = i;}return dfs(0,0,n-1);}
};