Codeforces Round 892 (Div. 2)-编程知识

A.最大值只能由自己除，所以无解的情况只能是全部相同，否则直接最大值放c即可

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;int n,m,k;
int a[N],b[N];void solve(){set<int> st;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];st.insert(a[i]);}if(st.size()==1) cout<<"-1\n";else{vector<int> c,d;auto mx=*st.rbegin();for(int i=1;i<=n;i++)if(a[i]==mx) c.push_back(a[i]);else d.push_back(a[i]);cout<<d.size()<<" "<<c.size()<<"\n";for(auto x:d) cout<<x<<" ";cout<<'\n';for(auto x:c) cout<<x<<" ";cout<<'\n';}}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();return 0;
}

B.b直接枚举其他数组的最小值放到当前数组（其他数组的最小值集中放在一个数组肯定最优的）

所以记录一下最小值和次小值即可

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
#define int long long
int n,m;
vector<int> a[N];
int mn1[N],mn2[N];
void solve(){cin>>n;int res=0;for(int i=1;i<=n;i++){cin>>m;a[i].clear();for(int j=1;j<=m;j++){int x;cin>>x;a[i].push_back(x);}sort(a[i].begin(),a[i].end());mn1[i]=a[i][0];mn2[i]=a[i][1];res+=mn1[i];}int mx=res;vector<int> mn(n+10,0x3f3f3f3f);for(int i=n;i>=1;i--) mn[i]=min(mn[i+1],mn1[i]);vector<int> s1(n+10,0);vector<int> s2(n+10,0);for(int i=1;i<=n;i++) s1[i]=s1[i-1]+mn1[i],s2[i]=s2[i-1]+mn2[i];vector<int> l(n+10,0x3f3f3f3f);vector<int> r(n+10,0x3f3f3f3f);for(int i=1;i<=n;i++) l[i]=min(l[i-1],mn1[i]);for(int i=n;i>=1;i--) r[i]=min(r[i+1],mn1[i]);for(int i=1;i<=n;i++){int now=s2[n]-mn2[i]+min({mn1[i],l[i-1],r[i+1]});mx=max(mx,now);}cout<<mx<<"\n";
}signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}

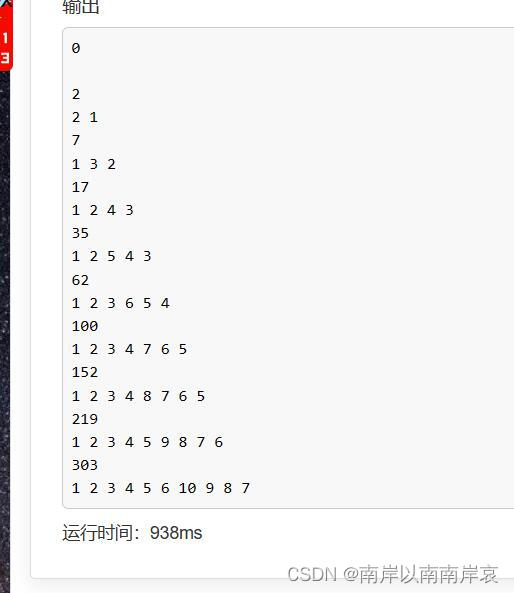
额直接打表看的规律，直接调用next_permuatation 打表前10个答案的数组，观察一下可得

前半部分按顺序，后半部分翻转即可

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
#define int long long
int n,m;
//int a[N];
int b[N];
void solve(){cin>>n;if(n==2){cout<<2<<"\n";return ;}int res=0;vector<int> s(n+10,0);vector<int> mx(n+10,0);for(int i=1;i<=n;i++){b[i]=i;s[i]=s[i-1]+b[i]*i;mx[i]=max(mx[i-1],b[i]*i);}for(int i=1;i<=n;i++){int now=s[i];int nw=n;int mxx=0;for(int j=i+1;j<=n;j++){now+=nw*j;mxx=max(mxx,nw*j);nw--;}mxx=max(mxx,mx[i]);res=max(res,now-mxx);}cout<<res<<"\n";}signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}

如果当前点在[l,r]中，那么他可以通过跳跃到有交集的且比当前区间靠右的那个区间的b那里

比如起点在第一个区间，无论在哪个点都能跳到b1，如果在b1那么和他相交的下一个区间她也能跳到b2，因为相交l<=b1

如果在当前点>b1 那么她依然能跳到b1，且更大可能能跳到下一个区间，且它依然能利用b1这个点跳跃到下一个区间

所以其实能跳跃的区间范围是[l,b]，直接合并有交集的跳跃区间即可

所以可以直接预处理出当前点能往右跳到哪里，最后二分出当前询问的点在哪个区间，

我用的并查集合并的

还有个问题就是二分的时候按照左端点排序，二分出最靠右的区间r>=l

因为第一个红线和第二个红线其实已经合并了，但是都没r优，所以要二分出最靠右的区间r>=l

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;int n,m,k;
PII a[N];
class dsu {public:vector<int> p;vector<int> mx;int n;dsu(int _n) : n(_n) {p.resize(n);iota(p.begin(), p.end(), 0);mx.resize(n);}inline int get(int x) {return (x == p[x] ? x : (p[x] = get(p[x])));}inline bool unite(int x, int y) {x = get(x);y = get(y);if (x != y) {mx[y]=max(mx[x],mx[y]);p[x] = y;return true;}return false;}
};void solve(){cin>>n;dsu d(n+10);for(int i=1;i<=n;i++){int l,r,bb,aa;cin>>l>>r>>aa>>bb;a[i]={l,bb};}sort(a+1,a+1+n,[&](const auto&p,const auto&q){return p.first<q.first; });for(int i=1;i<=n;i++) d.mx[i]=a[i].second;for(int i=2;i<=n;i++){int l=a[i].first,r=a[i].second;int x=d.get(i-1),y=d.get(i);if(l<=d.mx[x]){d.unite(x,y);}}int q;cin>>q;while(q--){int x;cin>>x;int res=x;int l=1,r=n;while(l<r){int mid=l+r+1>>1;if(a[mid].first<=x) l=mid;else r=mid-1;}if(a[l].first<=x&&d.mx[d.get(l)]>=x){res=max(res,d.mx[d.get(l)]);}if(q)cout<<res<<" ";else cout<<res<<"\n";}
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();return 0;
}

E：

设f为前i个点，且当前线段长度总和为k的贡献最大值

复杂度是n*k*k，因为要枚举当前长度和上一个线段总和的长度

考虑优化把绝对值拆开

首先ai和bi已经枚举了，且下标一样，所以已经固定了，接下来就是维护另一个aj和bj

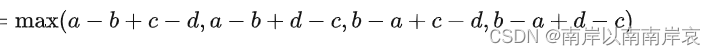
copy一下别人的，别人写的清晰

#include<bits/stdc++.h>
using namespace std;
const int N = 3010,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;int n,m,k;
int a[N],b[N];
int mx[2][2][N];
void solve(){cin>>n>>k;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];memset(mx,-0x3f,sizeof(mx));vector<vector<int>> f(n+10,vector<int>(k+10,0));for(int i=1;i<=n;i++){for(int j=1;j<=min(i,k);j++){for(int x=0;x<2;x++){for(int y=0;y<2;y++){mx[x][y][i - j] = max(mx[x][y][i - j], f[i - 1][j - 1] + (x == 0 ? a[i] : -a[i]) + (y == 0 ? b[i] : -b[i]));}}for(int x=0;x<2;x++){for(int y=0;y<2;y++){f[i][j]=max(f[i][j],f[i-1][j]);f[i][j]=max(f[i][j],mx[x][y][i-j]+ (x == 0 ? -b[i] : b[i]) + (y == 0 ? -a[i] : a[i]));}}}}cout<<f[n][k]<<"\n";}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();return 0;
}