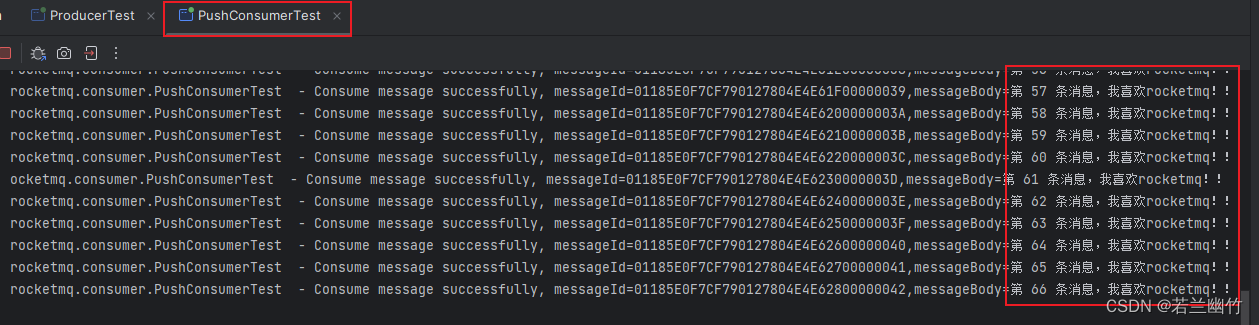
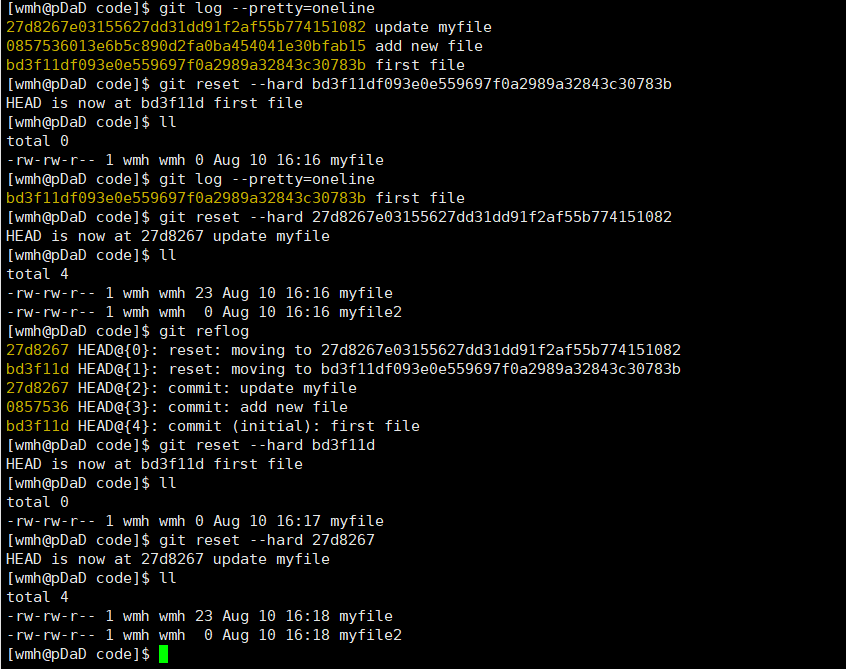
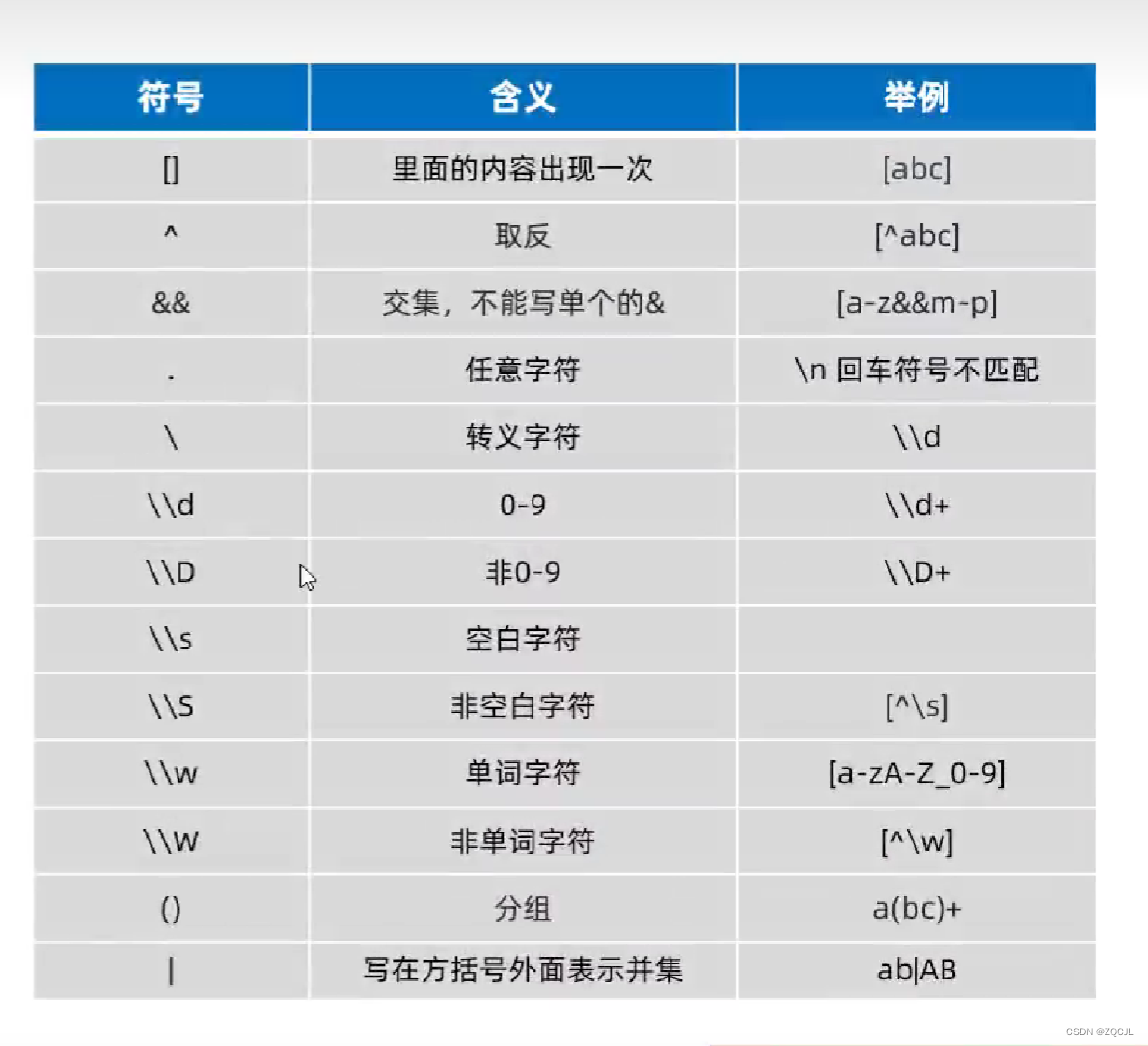
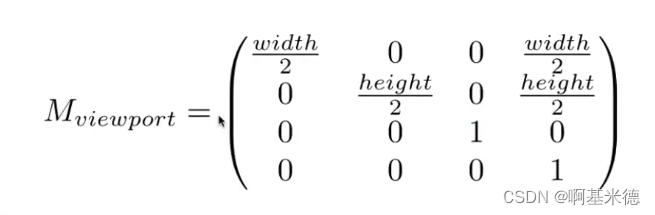三种解决方案
这个问题提出的时候,Milvus 的最新版本是 2.2.8,我们做个角色互换,在当时站在这个用户的角度,留在我们面前的选择有这么几个:

-
为每个租户创建一个 collection
-
为每个租户创建一个 partition
-
创建一个租户名称的标量字段
接下来,我们依次分析下这三种方案的可行性:
-
方案 1:为每个租户创建一个 collection。
这是我们最自然想到的方式,非常直观,使用也最简单,但是它有一个致命缺点,Milvus 的一个集群里面最多只能创建 65536 个集合。之所以有这个限制,是因为 Milvus 里的集合是和消息系统(Pulsar/Kafka)的 topic 绑定的,Pulsar/Kafka 的 topic 有数量上限,集合数量过多之后,topic 的复用率也会很高,会导致严重的读放大问题。因为我们有 10K - 20K 个租户,所以每个租户一个集合的方式走不通了。
不过好消息是,社区里面已经在筹划引入一些更轻量的消息系统(NATS),集合数量有望在未来达到更高的水平。假如集合数量的问题能够解决,能达到像 MySQL 那样上亿的表数目上限