前言

😉大家好，我是向阳花，CSDN全栈领域新星创作者一枚😉。

在上一节中我们讲到了使用Matplotlib绘图配置的各项配置，如果没有看这篇文章的朋友，建议先学习这篇文章：一文搞定Matplotlib绘图配置（大三学长的万字笔记）

那么接下来，我们就开始使用 Matplotlib 进行各种基础图形的绘制。此外，我们还可以参考官网：matplotlib官网，进行绘制更多图象，结合文档学习，也是程序员们的一项重要技能哦！

在绘图之前，我们还是把相应的包导入，还有配置做好：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

# 当浏览器不显示绘图图片时，加上这一行
%matplotlib inline# 让图片可以显示中文
plt.rcParams['font.sans-serif'] = 'SimHei'
# 让图片可以显示负号
plt.rcParams['axes.unicode_minus'] = False# 支持svg矢量图
%config InlineBackend.figure_format = 'svg'

一、折线图

折线图可以显示随时间（根据常用比例设置）而变化的连续数据，用折线的升降来体现数据变化的趋势。

下面我们来绘制折线图。

1 - 单线

fig = plt.figure(figsize=(4,3))# 数据
x = [2018,2019,2020,2021,2022,2023]
y = [40,30,20,80,50,60]# 绘制折线图
plt.plot(x,y,c='g',marker='D',markersize=3)# 添加标签
plt.xlabel('年份')
plt.ylabel('报名人数')# 添加标题
plt.title('某活动报名人数',fontsize=10)# 添加文本
for a,b in zip(x,y):plt.text(x=a+0.3,y=b+0.5, # 根据(x,y)坐标确定文本的位置s=b, # 文本内容ha='center', # 水平对齐方式va='center' # 垂直对齐方式)

2 - 多线

当 plot() 函数只接收了一个数据时，那么X轴范围是 0-N（N是数据个数）。

fig = plt.figure(figsize=(4,3))x = np.random.randint(0,10,15)# 当 plot() 函数只接收了一个数据时，那么X轴范围是0-N（N是数据个数）
plt.plot(x,marker='*',c='r')
# cumsum：计算X的累加和
plt.plot(x.cumsum(),marker='o',c='b')plt.xlabel('X')
plt.ylabel('Y')
plt.title('Change Trend')

二、柱状图（条形图）

柱状图利用柱子的高度，来反映数据的差异，也可用于比较数据的变化趋势。条形图和柱状图类似，是横向柱状图。

1 - 单柱

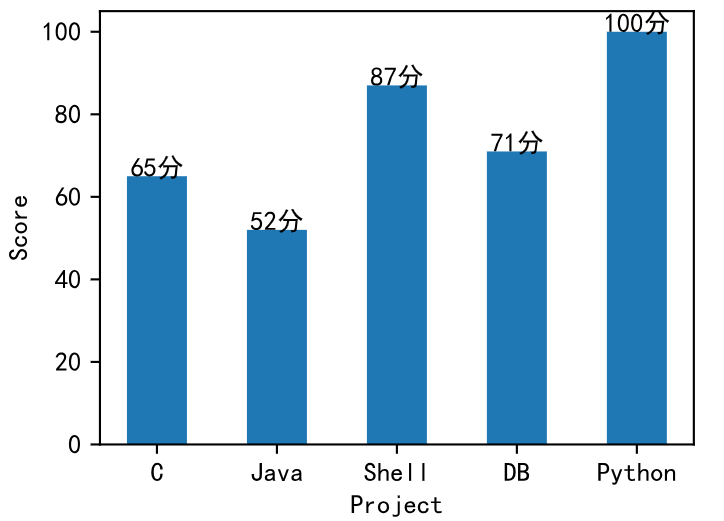
单柱即只绘制一种颜色的柱子（只有一类数据）。

# make data
x = ['C','Java','Shell','DB','Python']
y = [65,52,87,71,100]# figure
fig = plt.figure(figsize=(4,3))# labels
plt.xlabel('Project',fontsize=10)
plt.ylabel('Score',fontsize=10)# add text
for a,b in zip(x,y):plt.text(x=a,y=b+2,s="{}分".format(b),ha='center',va='center')
# plot
plt.bar(x,y,width=0.5)

2 - 多柱

多柱即一次绘制多个柱状图，也称为簇状柱形图。

fig = plt.figure(figsize=(4,3))# make data
x = np.arange(2015,2024)
y1 = make_random()
y2 = make_random()# 每一个柱子的宽度
# (默认值是0.6，我们要分为两个柱子，那么每一个柱子占0.3)
width = 0.3# ticks
plt.xticks(x)
plt.yticks(np.arange(11))# plot(x-width/2是将柱子往左移动)
plt.bar(x-width/2,y1,color='orange',width=width)
plt.bar(x+width/2,y2,color='green',width=width)

绘制效果如下：（因为是随机数，所以每个人绘制的效果是不一定一样的）

3 - 堆叠

首先编写生成随机数的函数：

def make_random():return np.random.randint(5,10,9)

接下来绘制两个柱状图：

fig = plt.figure(figsize=(4,3))# make data
x = np.arange(2015,2024)
y1 = make_random()
y2 = make_random()# plot
plt.bar(x,y1,color='b')
plt.bar(x,y2,color='g')

绘制结果如下：

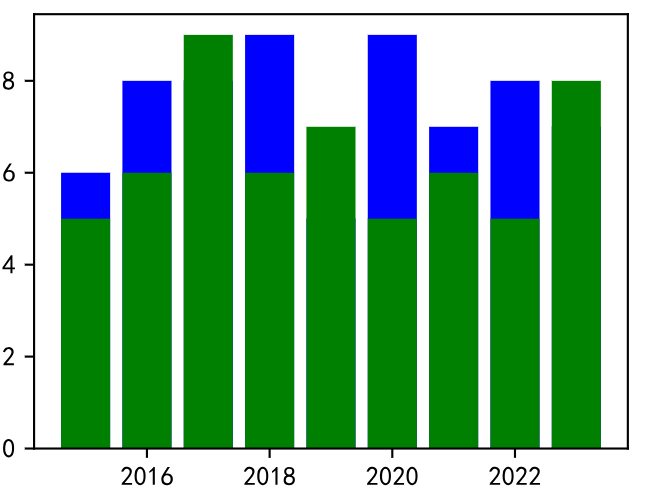
我们会发现，虽然现在柱状图是堆叠的，但是有些蓝色部分被绿色部分完全挡住了，根本看不出来它的值是多少，所以说这样绘制肯定是不可取的，我们需要对代码进行修改。

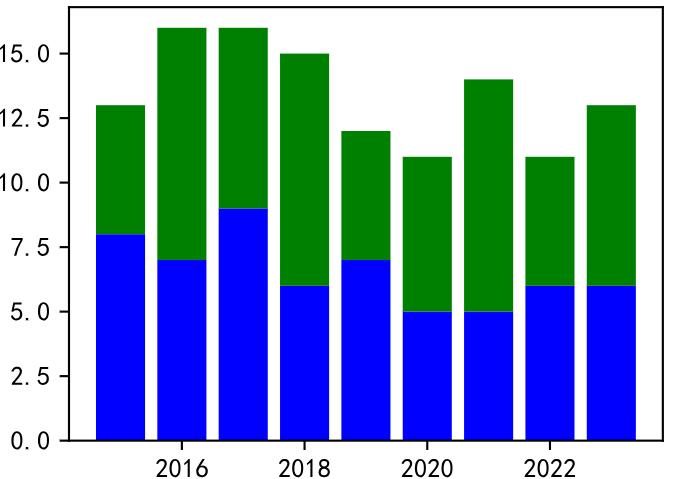
其实，要实现堆叠效果，就是让第二次绘图时，Y2轴的取值建立在Y1之上，也就是对每一个Y2+Y1，所以我们只需要修改最后一行，加上 bottom 参数，这样即可实现堆叠效果。

plt.bar(x,y2,color='g',bottom=y1)

4 - 条形

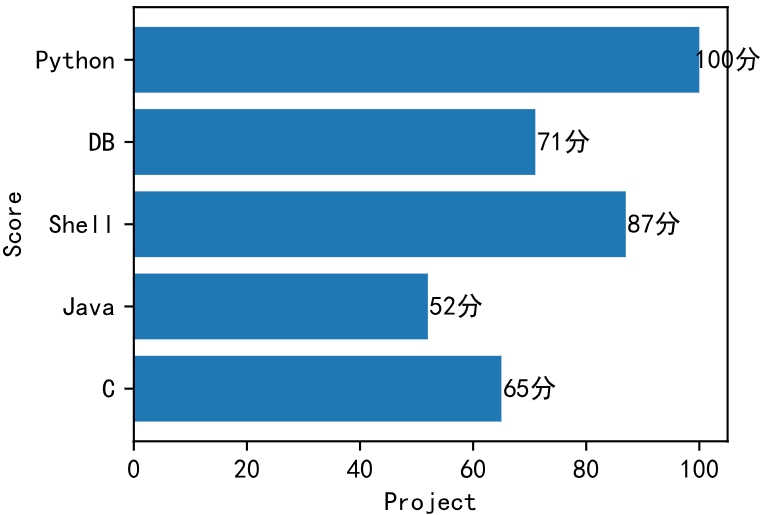
条形图是水平方向的柱状图，和柱状图绘图方法类似，使用的是 barh() 方法。

# make data
x = ['C','Java','Shell','DB','Python']
y = [65,52,87,71,100]# figure
fig = plt.figure(figsize=(4,3))# labels
plt.xlabel('Project',fontsize=10)
plt.ylabel('Score',fontsize=10)# add text
for a,b in zip(y,x):plt.text(x=a+5,y=b,s="{}分".format(a),ha='center',va='center')
# plot
plt.barh(x,y)

三、直方图

直方图描述的是一组数据的出现次数分布。直方图有助于我们知道数据的分布情况，诸如众数、中位数的大致位置、数据是否存在缺口或者异常值。

fig = plt.figure(figsize=(4,3))# make data
x = np.random.randint(0,11,100) # 1-10# plot
plt.hist(x)
plt.show() # instantly show，no print other.

此外，还可以对直方图进行分组。

分组的意思就是划分区间，比如说[0-2]一组，那么在0-2范围内的数据都会被统计进来，作为一类数据。hist() 方法的 bins 参数就是用来分组的。

fig = plt.figure(figsize=(4,3))# make data
x = np.random.randint(0,11,100) # 1-10# divide groups
# 划分为4组，因为X取值范围是0-10，所以就是0-2.5,2.5-5,5-7.5,7.5-10这四组
bins = 4 # ticks
plt.xticks(x)
# plot
plt.hist(x,bins=bins)
plt.show() # instantly show，no print other.

四、箱型图

箱型图，它能显示处一组数据的最大值，最小值，中位数，上下四分位数以及异常值。

1 - 单个

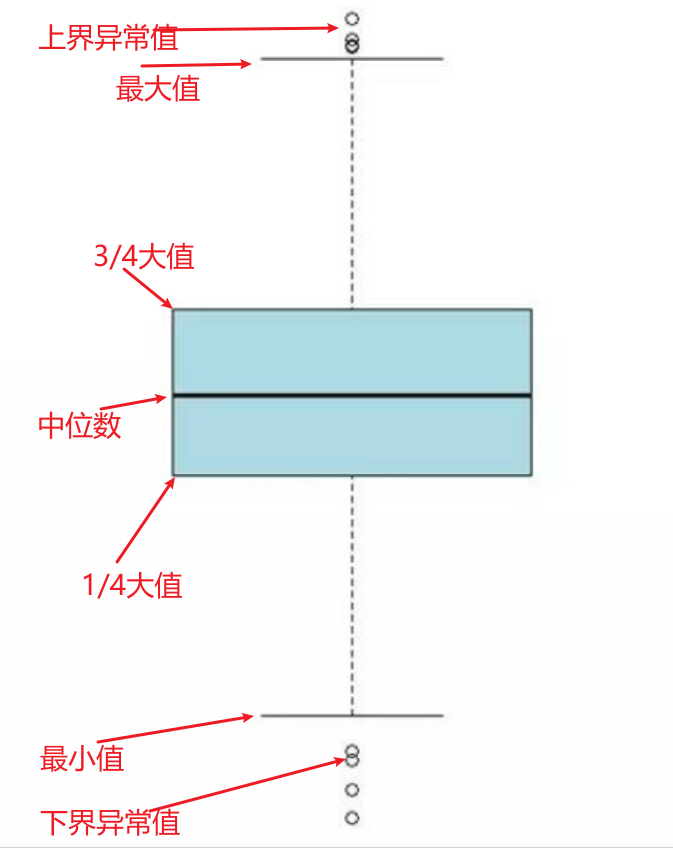
fig = plt.figure(figsize=(4,3))x = [1,3,2,5,10,-10,23]plt.boxplot(x)
plt.show()

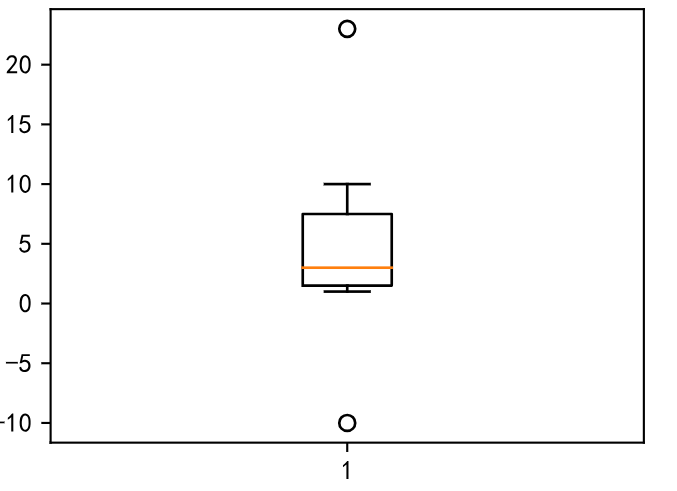
上面的图中即包含了各种情况，那么什么样的数据会被判断为异常值？

异常值（用字母 K 表示），分为中度异常（K = 1.5）和重度异常（K = 3），有一个计算方法如下。

设：QL(下四分位数)，QU(上四分位数），IQR（QU - QL）。那么中度异常
就是小于：
$$QL-1.5IQR$$
或者大于：
$$QU+1.5IQR$$
重度异常同理，将1.5换成3即可。

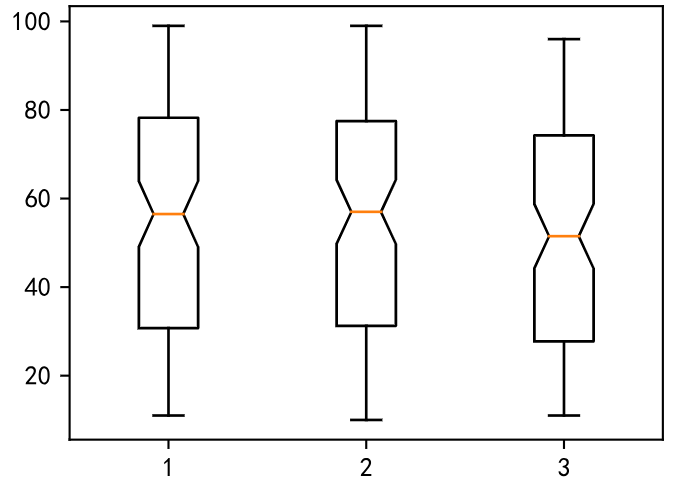
2 - 多个

一次画多个箱型图，只需要为 boxplot() 函数传递一个列表即可。

fig = plt.figure(figsize=(4,3))x1 = np.random.randint(10,100,100)
x2 = np.random.randint(10,100,100)
x3 = np.random.randint(10,100,100)plt.boxplot(x = [x1,x2,x3],notch=True, # change a style)
plt.show() # instantly show,no print other.

五、散点图

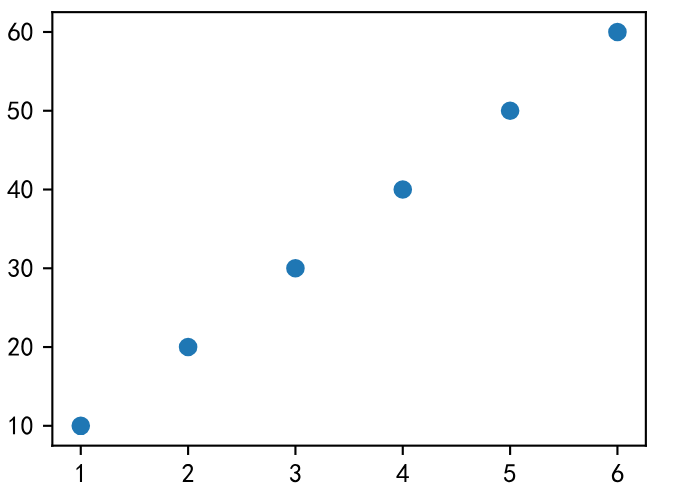
1 - 散点图

散点图用于在水平轴和纵轴上绘制数据点，它表示了因变量随自变量变化的趋势。通俗的讲，它反映Y轴变量受X轴变量的影响程度。

fig = plt.figure(figsize=(4,3))x = range(1,7,1)
y = range(10,70,10)plt.scatter(x,y)

2 - 气泡图

它与散点图类似，绘制的时候，将一个变量放在横轴，另一个变量放在纵轴，而第三个变量则表示很多泡泡的大小（这意味着它是一个可迭代对象）。

fig = plt.figure(figsize=(4,3))# Create a sample from the "standard normal" distribution.
data = np.random.randn(100,2)# An array of bubble sizes
size = np.random.randint(50,200,100)# An array of bubble colors
color = np.random.randn(100)# plot
plt.scatter(x=data[:,0],y=data[:,1],s=size,c=color,alpha=0.5
)

六、饼图

1 - 饼图

饼状图用来显示一个数据系列，具体来说，饼状图显示一个数据系列中各项占项目总和的百分比。

plt.figure(figsize=(4, 3))# make data
x = np.random.randint(10,30,5)
citys = ['Beijing','Shanghai','Shenzhen','Nanjing','Guangzhou']plt.pie(x=x,autopct='%.1f%%', # 显示百分比pctdistance=0.6, # 文字距离圆心的距离labels=citys, # 标签labeldistance=1.3, # 标签距离圆心的位置textprops={'fontsize':12,'color':'black'}, # 文字样式explode=[0,0,0.05,0,0.09], # 分裂效果shadow=True # 阴影效果
)plt.show()

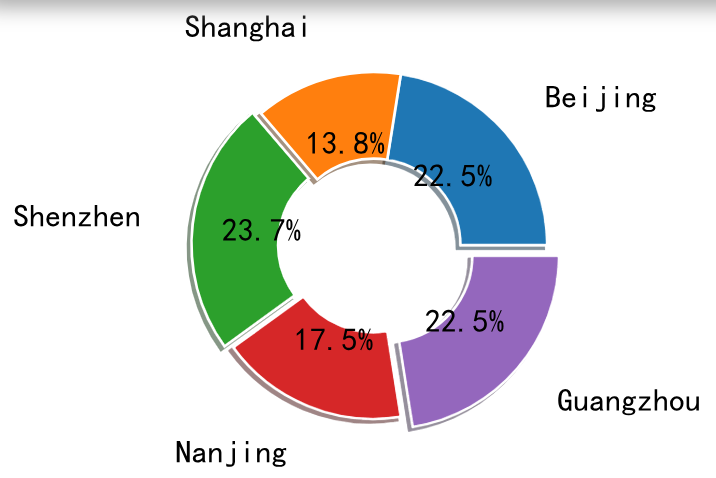
2 - 甜甜圈 | 空心

要绘制甜甜圈，只需要加上一个 wedgeprops 属性即可。

甜甜圈设置的原理就是通过设置饼状图的饼的宽度，宽度初始值为1，此时是占满了整个圆的，如果小于1，那么就是圆环状了。

plt.figure(figsize=(4, 3))# make data
x = np.random.randint(10,30,5)
citys = ['Beijing','Shanghai','Shenzhen','Nanjing','Guangzhou']plt.pie(x=x,autopct='%.1f%%', # 显示百分比pctdistance=0.6, # 文字距离圆心的距离labels=citys, # 标签labeldistance=1.3, # 标签距离圆心的位置textprops={'fontsize':12,'color':'black'}, # 文字样式explode=[0,0,0.05,0,0.09], # 分裂效果shadow=True, # 阴影效果wedgeprops={'width': 0.5,'edgecolor':'w'} # 甜甜圈设置
)plt.show()

3 - 甜甜圈 | 实心

实心甜甜圈的原理就是，外面的圆环使用的是空心甜甜圈，里面的圆是正常画的饼图，只不过，里面的饼图刚好填充了甜甜圈的内部空白区域，通过设置 radius 可以达到，下面请看代码示例。

plt.figure(figsize=(6, 4))# make data
citys = ['Beijing','Shanghai','Shenzhen','Nanjing','Guangzhou']
x1 = np.random.randint(10,30,5)
x2 = np.random.randint(10,30,5)# 第一个圆环
plt.pie(x=x1,autopct='%.1f%%', # 显示百分比pctdistance=0.6, # 文字距离圆心的距离labels=citys, # 标签labeldistance=1.3, # 标签距离圆心的位置wedgeprops={'width': 0.4,'edgecolor':'w'} # 甜甜圈设置
)# 第二个圆环，用来填充空白处
plt.pie(x=x2,autopct='%.1f%%', # 显示百分比pctdistance=0.6, # 文字距离圆心的距离radius=0.6 # 设置圆的半径，从而使该圆刚好填充空白区域
)plt.show()

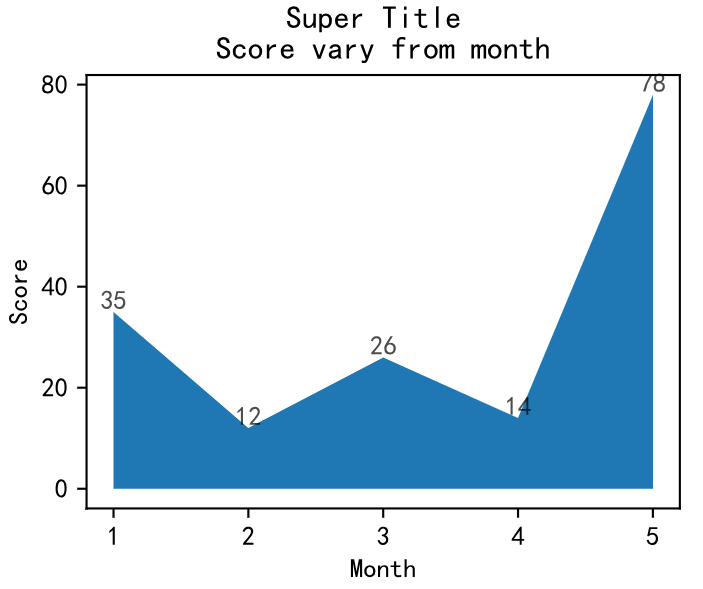
七、面积图

面积图又称为区域图，和折线图类似，用于强调Y轴随X轴而变化的程度，可用于引起人们对总值趋势的注意。

fig = plt.figure(figsize=(4,3))x = [1,2,3,4,5]
y = np.random.randint(10,100,5)# label
plt.xlabel('Month')
plt.ylabel('Score')# title
plt.title('Score vary from month')
plt.suptitle('Super Title',y=1)
# plot
plt.stackplot(x,y)# text
for a,b in zip(x,y):plt.text(x=a,y=b+2,s=b,fontsize=10,alpha=0.7,ha='center',va='center')# instantly show
plt.show()

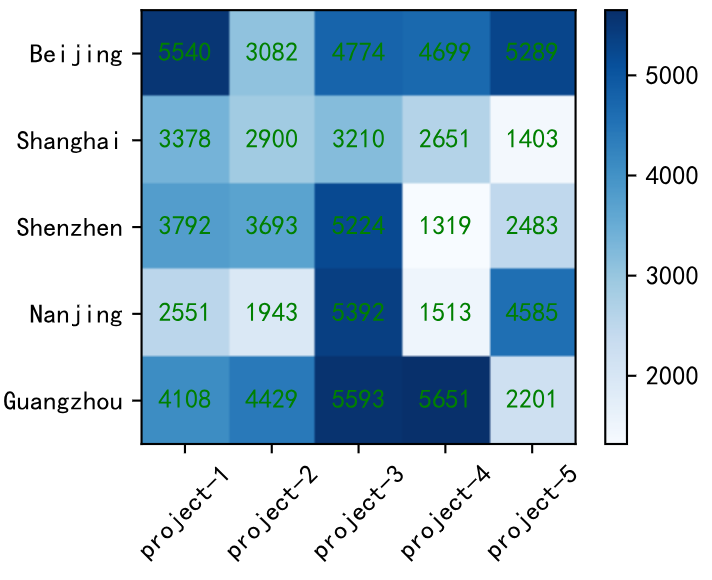
八、热力图

热力图是一种通过对色块着色来显示数据的统计图表。

适用场景：

（1）热力图的优势在于“空间利用率高”，可以容纳较为庞大的数据。热力图不仅有助于发现数据间的关系、找出极值，也常用于刻画数据的整体样貌，方便在数据集之间进行比较（例如将每个运动员的历年成绩都浓缩成一张热力图，再进行比较）。

（2）如果将某行或某列设置为时间变量，热力图也可用于展示数据随时间的变化。例如，用热力图来反映一个城市一年中的温度变化，气候的冷暖走向，一目了然。

# figure
fig = plt.figure(figsize=(4,3))# make data
x = ["project-{}".format(i+1) for i in range(5)]
y = ['Beijing','Shanghai','Shenzhen','Nanjing','Guangzhou']
data = np.random.randint(1000,6000,(5,5))# ticks
plt.xticks(ticks=range(len(x)),labels=x,rotation=45)
plt.yticks(ticks=range(len(citys)),labels=citys)# add text
for i in range(len(x)):for j in range(len(y)):plt.text(x=i,y=j,s=data[j,i],ha='center',va='center',fontsize=10,color='g')
# plot
plt.imshow(data,cmap='Blues')# add side color bar
plt.colorbar()

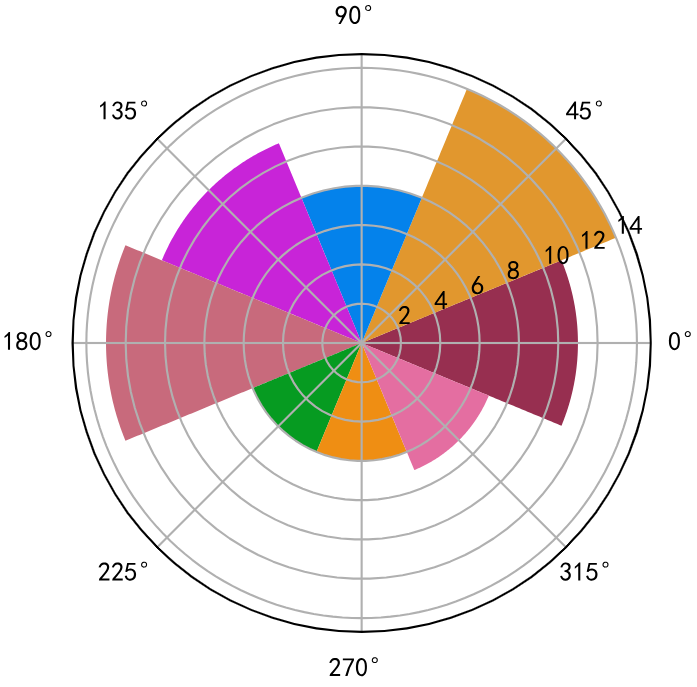
九、极坐标图

极坐标系是一个二维坐标系统，该坐标系统中任意位置可由一个夹角和一段相对原点的距离来表示。极坐标图（Polar）用来将极坐标系的信息表示出来的图形格式。

N = 8# create a arithmetic progression with eight number from 0 to 2*np.pi
x = np.linspace(0,2*np.pi,N,endpoint=False)
# the height of polar 
heiht = np.random.randint(3,15,size=N)# width
width = 2*np.pi / N
# color
color = np.random.rand(8,3) # rand:Return a array from 0 to 1.# plot
axes = plt.subplot(111,projection='polar')
axes.bar(x=x,height=heiht,width=width,bottom=0,color=color
)

十、雷达图

当我们需要综合评价多个变量或指标时，条形图或柱状图可能是我们的首选，涉及到多组间的比较时，可能就需要分组条形图或分组柱状图了。

有时候也不禁问自己，只有这一种选择吗？

今天，我们就说说另外一种数据展示的图表——雷达图。

在实际场景中，雷达图也用于描述一个人的能力。比如中国乒乓球员有一位被成为“六边形战士”的，这个六边形能力，就算用雷达图描述的。

雷达图其实就是放在极坐标系中的首尾相连的折线图。

plt.figure(figsize=(3,3))x = np.linspace(0,2*np.pi,6,endpoint=False)
y = [80,60,90,70,70,100]# 首尾相连
x = np.concatenate((x,[x[0]]))
y = np.concatenate((y,[y[0]]))# 绘制极坐标系
axes = plt.subplot(111,polar=True)# 绘制折线条
axes.plot(x,y,ls='-',lw=1,color='g')
# 填充
axes.fill(x,y,alpha=0.3)# 显示文本
for a,b in zip(x,y):plt.text(x=a,y=b+2,s=b,fontsize=10,color='r',ha='center',va='center')

十一、等高线图

等高线图，有时称为地形图，是在平面上用等高线表示的三维地貌。 该图显示鸟瞰图，允许人们直观地看到正在绘制的丘陵、山谷和斜坡。

在绘制等高线图之前，我们先来介绍一个 meshgrid(a,b) 方法，该方法将 a,b 变成相同形状（shape）的数组，并返回新的数组。

a = np.array([1,2,3])
b = np.array([4,5])# meshgrid(a,b)，将 a,b 变成相同形状的数组
A,B = np.meshgrid(a,b)
display(A,B)

下面我们来绘制等高线图：

fig = plt.figure(figsize=(4, 3))# make data
x = np.linspace(-5,5,100)
y = np.linspace(-5,5,100)# let x,y have same shape
X,Y = np.meshgrid(x,y)
Z = np.sqrt(X**2+Y**2)# plot
cb = plt.contourf(X,Y,Z)
# color bar
plt.colorbar(cb)
plt.show()

十二、3D图

在前面我们提到使用 matplotlib 也可以绘制3D图，下面我们就来绘制一些常见的3D图象。

下面的绘制方法，如果是 matplotlib-3.1.1 版本，会出现一系列类似下面的警告。

虽然说没有什么影响，但是有些不美观，因此，绘制3D图时可以参考官网的绘图案例去绘图。

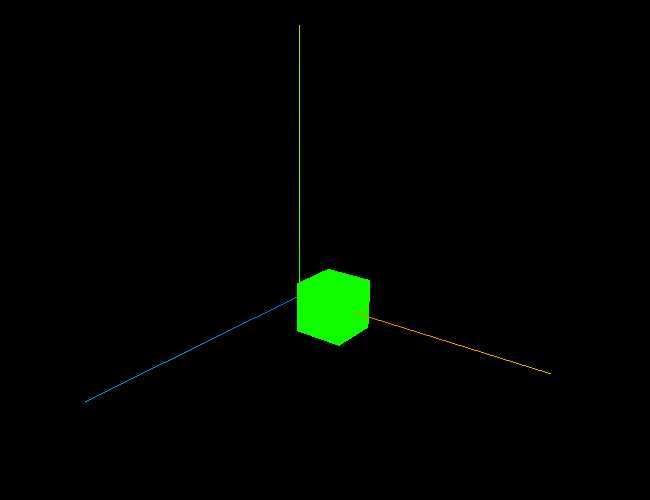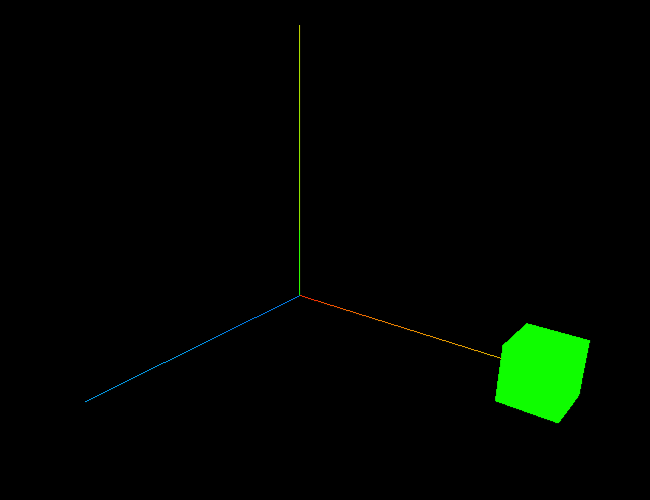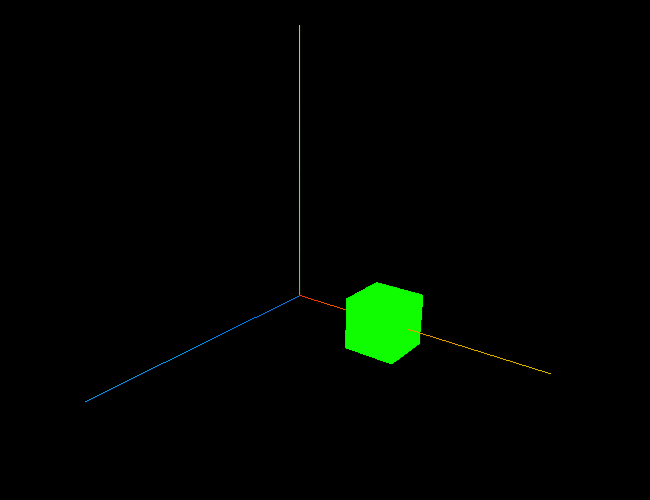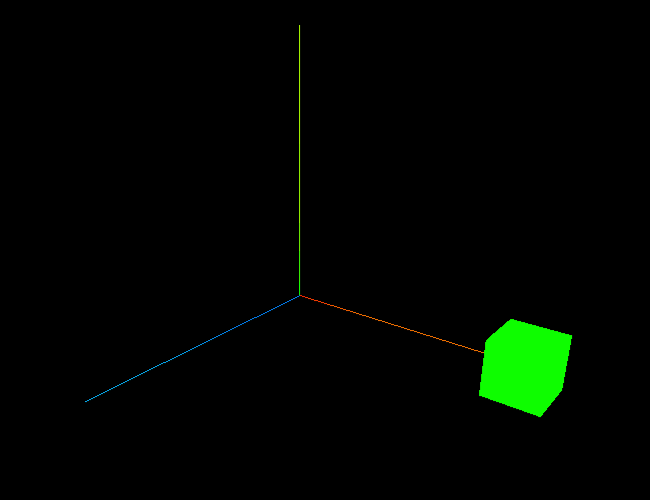
1 - 三维折线图

fig = plt.figure(figsize=(4, 3))# data
x = np.linspace(0,100,400)# image
y = np.sin(x)
z = np.cos(x)# 3D line chart
axes = Axes3D(fig)
fig.add_axes(axes)
axes.plot(x,y,z)plt.show()

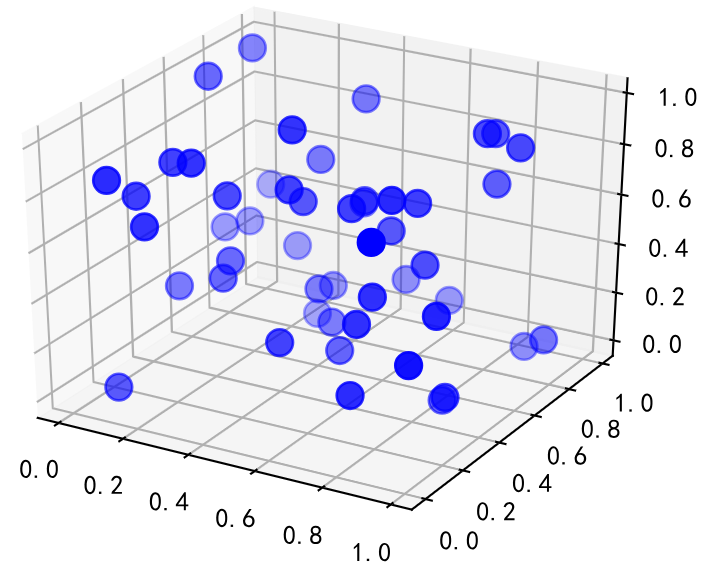
2 - 三维散点图

fig = plt.figure(figsize=(4, 3))axes = Axes3D(fig)
fig.add_axes(axes)# make data
x = np.random.rand(50)
y = np.random.rand(50)
z = np.random.rand(50)# plot scatter
axes.scatter(x,y,z,color='b',s=100)

3 - 三维柱状图

fig = plt.figure(figsize=(5, 4))axes = Axes3D(fig)
fig.add_axes(axes)x = np.arange(1, 5)for i in x:axes.bar(np.arange(4),np.random.randint(10, 100, size=4),zs=i,zdir='x',width=0.6,alpha=0.7)# label
axes.set_xlabel('X轴',fontsize=10,color='r')
axes.set_ylabel('Y轴',fontsize=10,color='g')
axes.set_zlabel('Z轴',fontsize=10,color='b')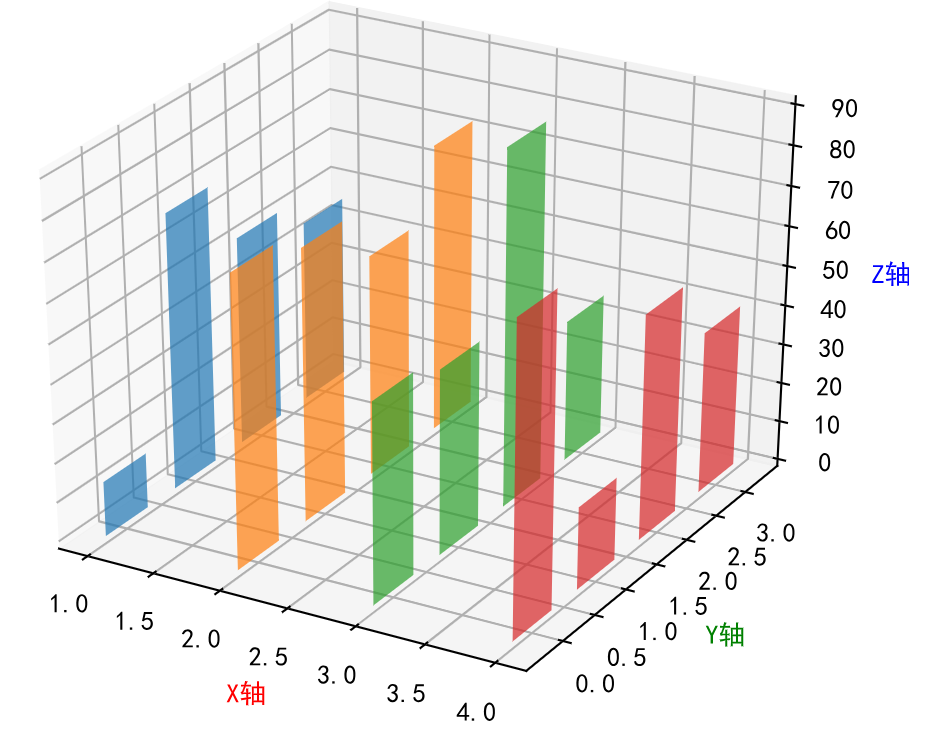

图象处理

• 读取图片

该方法返回一个 NumPy 数组。

n = plt.imread(r'F:\Pictures\图片素材\csdn封面\社区图片\听海.png')

• 显示图片

该方法传递一个 numpy 数组作为参数。

plt.imshow(n)

• 保存图片

该方法至少传递文件名和 numpy 数组作为参数。

plt.imsave('sea.jpg',n,dpi=200)

结语

以上就是本期要分享的全部内容了！综合来看，我们要善于查看方法帮助（将光表定位在方法的花括号中，然后按 Shift + Tab 即可。

我是向阳花，我在CSDN等你！🚀