0.常见位运算总结
1.基础位运算
<< >> ~
&:有0就是0
|:有1就是1
^:相同为0,相异为1/无进位相加
2.给一个数n,确定它的二进制表示中的第x位是0还是1
n & (1 << x) 结果为0就是0,结果不为0就是1。
3.将一个数n的二进制表示的第x位修改成1
n |= (1<<x)
4.将一个数n的二进制表示的第x位修改成0
n &= ~(1<<x)
5.位图的思想
位图本质就是一种哈希的思想,只是哈希是利用数组存放,位图是用一个变量来存放,即这个变量的比特位可以是0可以是1,2-4本质都是位图的。
6.提取一个数(n)二进制表示中最右侧的1
n & -n
-n:先对n取反再加1,会发现把最右侧的1,左边的区域全部变成相反。
7.干掉一个数(n)二进制表示中最右侧的1
n & (n - 1)
n - 1:将最右侧的1,右边的区域全部变为相反(包含1)。
8.位运算的优先级
能加括号就加括号就无需考虑优先级了。
9.异或(^)运算的运算律
a^0=a
a^a=0
a^b^c=a^(b^c)
1.位1的个数
位1的个数

思路:
利用n & (1 << i)结果是否为0来确定该位置是否为0或者1.
class Solution {
public:int hammingWeight(int n) {int cnt = 0;for(int i = 0; i < 32; i++)if((n & (1 << i))) cnt++;return cnt;}
};2.比特位计数
比特位计数

思路:
n &= (n - 1):干掉最右侧的1
class Solution {
public:int countOnes(int x){int cnt = 0;while(x > 0){//干掉最右侧的1x &= (x - 1);cnt++;}return cnt;}vector<int> countBits(int n) {vector<int> ans(n + 1);for(int i = 0; i <= n; i++){ans[i] = countOnes(i);}return ans;}
};3.汉明距离
汉明距离
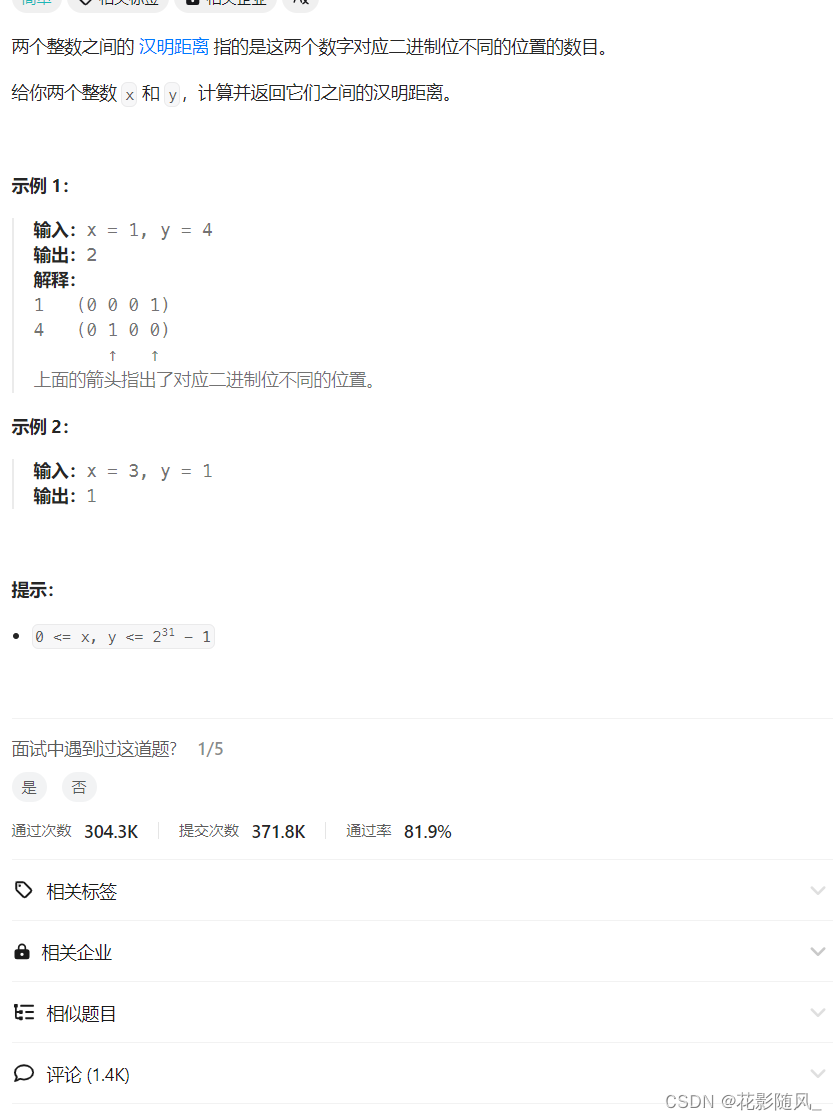
思路:
利用异或的相同为0,相异为1的规则,来计算两个数不同比特位的个数。
class Solution {
public:int hammingDistance(int x, int y) {int cnt = 0, s = x ^ y;while(s){cnt += s & 1;s >>= 1;}return cnt;}
};4.只出现一次的数字
只出现一次的数字
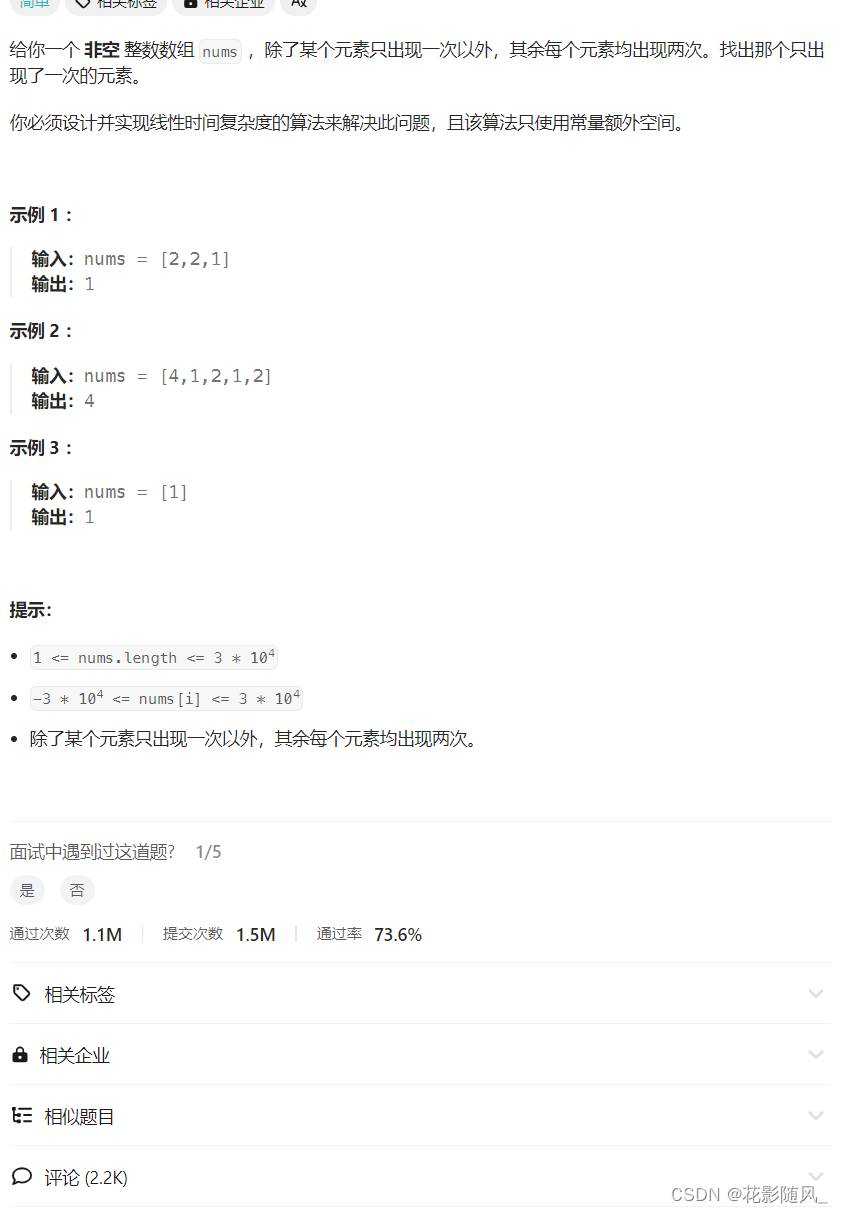
思路:
利用异或规律a^a = 0, a^0 = a;
出现偶数次的数最终都会被消除留下的1个数就是只出现一次的数字。
class Solution {
public:int singleNumber(vector<int>& nums) {int val = 0;for(auto e : nums)val ^= e;return val;}
};5.只出现一次的数字III
只出现一次的数字iii

思路:
有两个只出现一次的数字
则可分组求出,以数组异或和的最右侧1为分界分组
把这个最右侧的1提取出来用的是n & -n
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {int sum = 0;int res1 = 0;int res2 = 0;for(int i = 0; i < nums.size(); i++){sum ^= nums[i];}// 提取sum最右侧的1,同时为了防溢出int index = (sum == INT_MIN ? sum : (sum & -sum)); for(int e : nums){if(e & index) res1 ^= e;else res2 ^= e;}return {res1, res2};}
};6.判定字符是否唯一
判定字符是否唯一
思路:
解法一:哈希表
解法二:位图
运用位图的思想看这个字符加入位图之前是否有这个字符,有的话说明这个字符不唯一,那就返回false
class Solution {
public:bool isUnique(string astr) {//位图0-25 -> a-zint bitMap = 0;//鸽巢原理-》小优化if(astr.size() > 26) return false;for(char ch : astr){int i = ch - 'a';// 判断字符是否在位图中if(((bitMap >> i) & 1) == 1) return false;// 将字符进入位图bitMap |= (1 << i);}return true;}
};7.丢失的数字
丢失的数字

思路:
解法一:哈希表
解法二:高斯求和
解法三:位运算
利用异或运算规律求解。
class Solution {
public:int missingNumber(vector<int>& nums) {int ret = 0;for(int i = 0; i < nums.size(); i++) ret ^= nums[i];for(int i = 0; i <=nums.size(); i++) ret ^= i;return ret;}
};8.两整数之和
两整数之和

思路:
运用的是异或的无进位相加的性质,注意c++代码需要防溢出
a&b算进位,当进位为0时a就是最终结果。
class Solution {
public:int getSum(int a, int b) {//进位为0时结束while(b != 0){int x = a ^ b; //a与b无进位相加unsigned int carry = (unsigned int)(a & b) << 1;//算出进位,防止溢出a = x;b = carry;}return a;}
};9.只出现一次的数字ii
只出现一次的数字ii

思路:
利用位图的思想,每个比特位的和的规律得出。
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0; i < 32; i++){int sum = 0;//计算数组中当前位置的比特位之和for(auto x : nums)if(((x >> i) & 1) == 1) sum++;//比特位之和是3的倍数当前位置修改为0,否则修改为1sum %= 3;if(sum == 1) ret |= (1 << i);}return ret;}
};10. 消失的两个数字
消失的两个数字
思路:
与丢失的数字和只出现一次的数字iii结合,就是这个题的思路
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {int sum = 0;//通过两次循环异或得到的sum就是缺失的两个数的异或结果sum = a^bfor(auto x : nums) sum ^= x;for(int i = 1; i <= nums.size() + 2; i++) sum ^= i;//找出右侧第一个比特位为1,即a和b在这个位置的比特位不同的那个位置int diff = 0;while(1){if(((sum >> diff) & 1) == 1) break;diff++;}//根据diff的不同,将数组划分为两类来异或int a = 0, b = 0;for(auto x : nums){if(((x >> diff) & 1) == 1) a ^= x;else b ^= x;}for(int i = 1; i <= nums.size() + 2; i++){if(((i >> diff) & 1) == 1) a ^= i;else b ^= i;}return {a, b};}
};