1.树形结构
1.1概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把他叫做树是因为它看起来像一棵倒挂的树,也就说它的根朝上,而叶朝下的。它具有以下的特点:
- 有一个特殊的节点,称为根节点,根节点没有前驱节点
- 除根节点外,其余节点被分成M(M>0)个互不相交的集合T1,T2,T3,...,Tm,其中每一个集合Ti(1<=i<=m)又是一棵与树类似的子树。每棵子树的根节点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的

1.2关于树的一些重要概念
节点的度:一个节点含有的子树的个数称为该节点的度,如上图:A的为6
树的度:一棵树中,最大的节点的度称为树的度,如上图:树的度为6
叶子节点或终端节点:度为0的节点称为叶节点,如上图:B,C,H,I...等节点为叶节点
双亲节点或父亲节点:若一个节点含有子节点,则这个节点称为其子节点的父节点,如上图:A是B的父节点
孩子节点或子节点:一个节点若含有的子树的根节点称为该节点的子节点,如上图:B是A的孩子节点
根结点:一棵树中没有双亲结点的结点
节点的层次:从根开始定义起,根为第一层,根的子节点为第二层,以此类推
树的高度或深度:树中节点的最大层次,如上图:树的高度为4
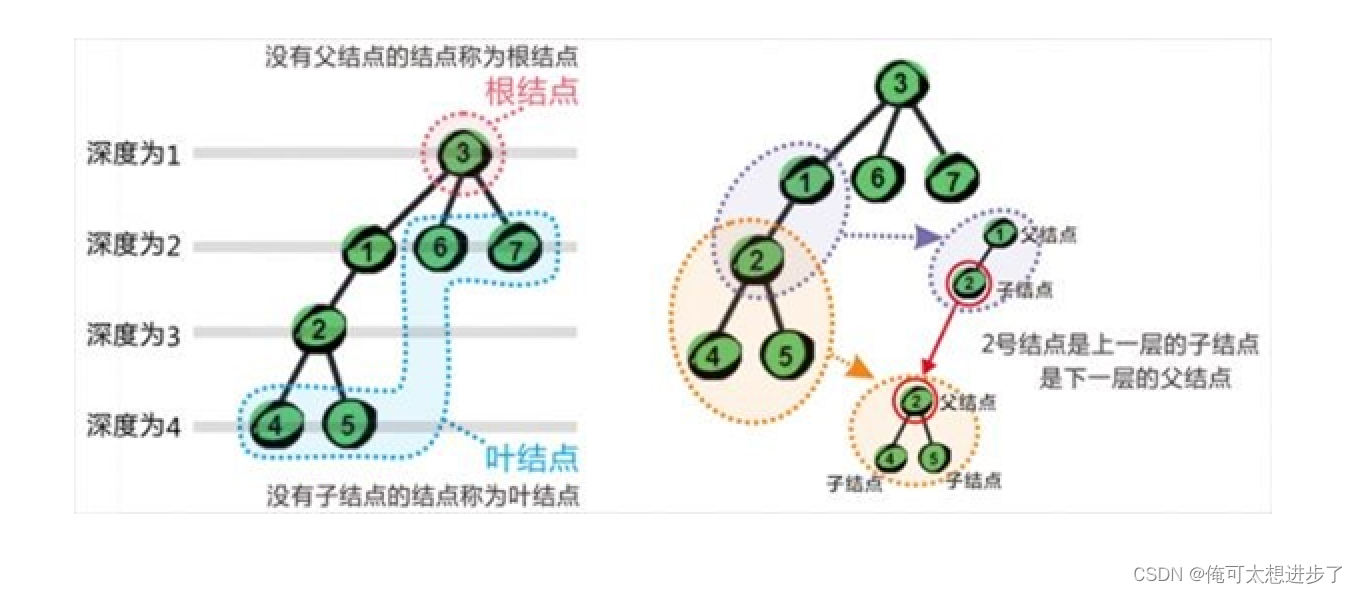
非终端节点或分支节点:度不为0的节点,如上图:D,E,F,G...等节点为分支节点
兄弟节点:具有相同父亲节点的节点互为兄弟节点,如上图:B,C互为兄弟节点
堂兄弟节点:双亲在同一层的节点互为堂兄弟,如上图:H,I互为堂兄弟节点
节点祖先:从根到该节点所经分支上的所有节点,如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙,如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
1.3树的表示形式(Java)
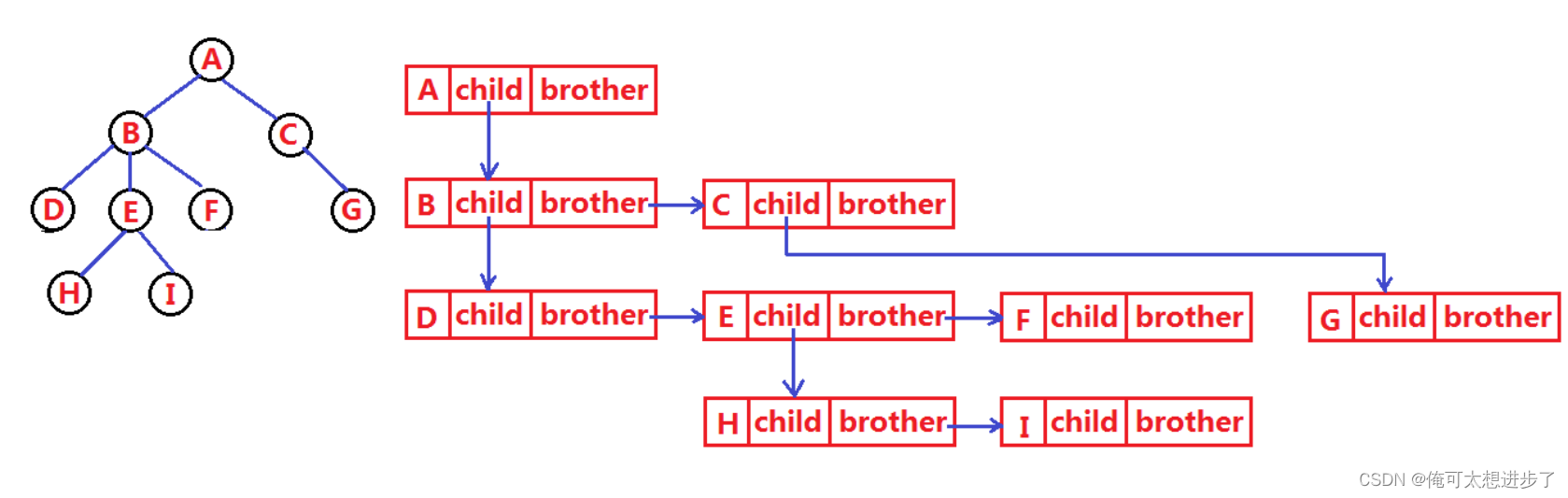
树的结构相对于线性表就比较复杂了,要储存表示起来就比较麻烦了,实际中树有很多表示方式,如:双亲表示法,孩子兄弟表示法等等。这里我们了解一下最常用的孩子兄弟表示法。
class Node {
int value; //树中存储的数据
Node firstChild; //第一个孩子引用
Node nextBrother; //下一个兄弟引用
}
1.4树的应用
文件系统是操作系统中负责管理文件存储和访问的组成部分,而树结构在这一领域中扮演着至关重要的角色。以下是树在文件系统管理中的几个关键应用:
- 目录结构:文件系统中的目录和子目录通常被组织成树形结构。这种层次化的组织结构使得文件的分组和管理变得直观且高效。每个目录可以看作是树中的一个节点,子目录和文件则作为其子节点。这样的结构方便用户对文件进行分组,并且能够清晰地表示出文件之间的层级关系。
- 文件索引:在更复杂的文件系统中,比如那些需要快速数据检索的系统中,会使用特殊的树形数据结构,例如B树或B+树。这些数据结构能够提供快速的查找、插入和删除操作。它们常用于构建文件系统的索引,帮助提高访问和检索文件的速度。
- 空间分配:某些文件系统会利用树结构来管理磁盘空间的分配。例如,在文件系统中,磁盘空间可以被划分为一个个区块(block),而这些区块可以通过树形结构来组织,从而高效地管理和分配磁盘空间。
- 文件系统元数据管理:文件系统的元数据,如文件大小、创建时间、修改时间等信息,也需要得到有效管理。树结构在这里同样发挥作用,它可以帮助维护这些元数据的有序性和可查询性。
- 稳定性与可靠性:自平衡的树结构,如AVL树或红黑树,可以确保在频繁的文件增加、删除操作下,文件系统的性能仍然保持稳定。这对于保持文件系统的响应速度和可靠性至关重要。
- 支持并发操作:现代文件系统往往需要支持多任务环境下的并发访问。某些树结构设计,如读写锁或版本控制机制,可以集成到文件系统中,以安全地处理并发操作,防止数据损坏。
- 容错与恢复:在分布式文件系统中,树结构有助于实现数据的冗余存储和容错处理。通过适当的复制和分布策略,即使在硬件故障的情况下也能保证数据的安全和完整性。
- 优化存储效率:某些树结构能够帮助文件系统优化存储空间的使用。例如,通过合理地组织数据以减少碎片,或者动态调整存储结构以适应不断变化的数据量和访问模式。
- 支持多种文件系统特性:包括快照、克隆以及远程同步等高级功能,都可能依赖于树结构来实现其核心逻辑。
- 兼容性与标准化:由于树结构在文件系统设计中的普遍应用,它有助于不同操作系统和应用程序之间实现更好的兼容性和标准化。
总的来说,树结构在文件系统的设计和管理中发挥着多方面的作用,从基本的目录管理到高级的数据索引和存储优化,都离不开这种灵活而强大的数据结构。
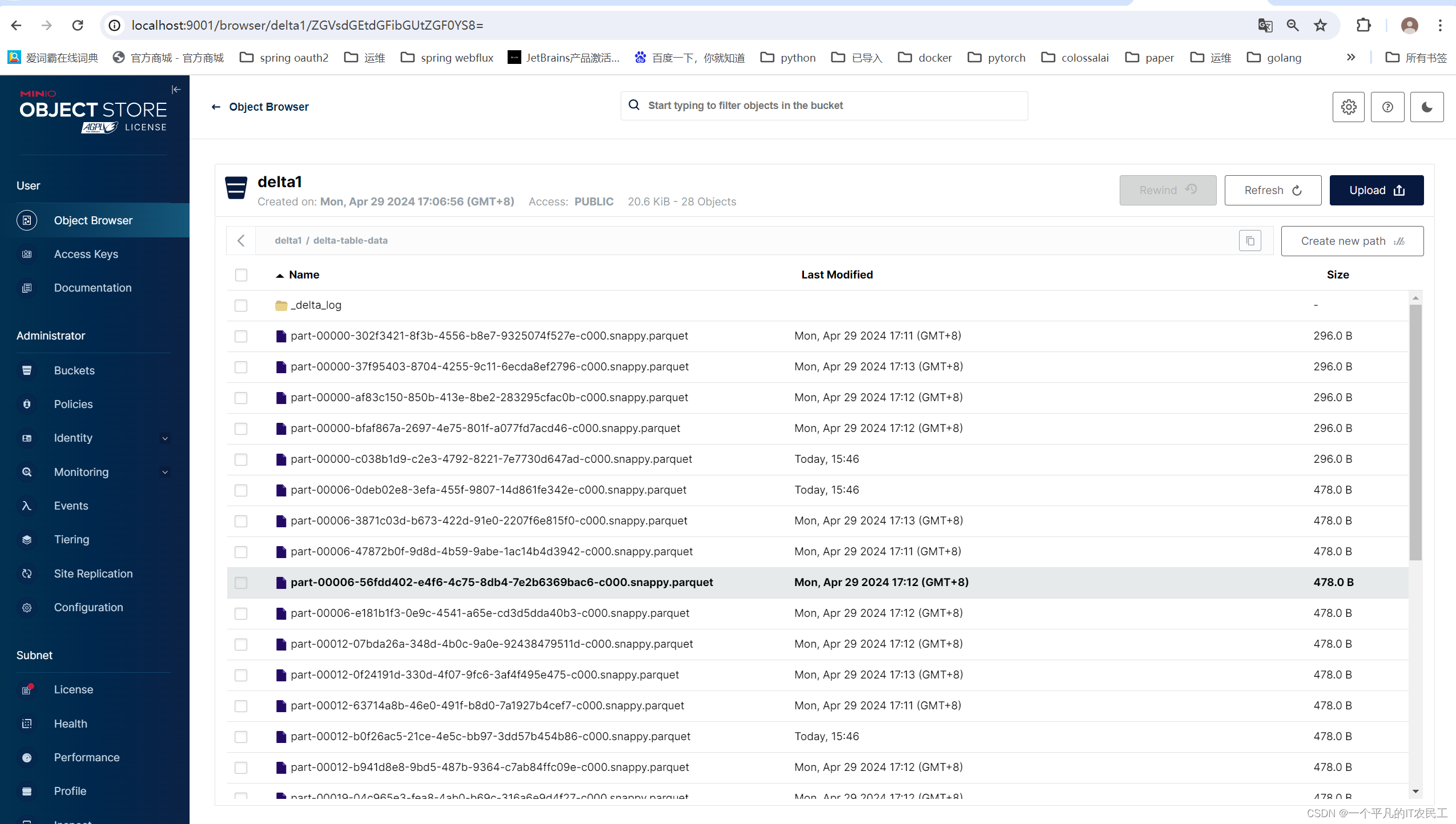
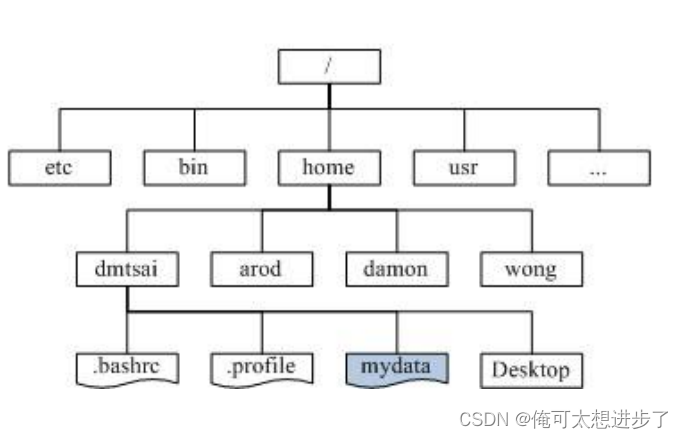
Linux的文件系统管理:
2.二叉树
2.1概念
一棵二叉树是节点的一个有限集合,或者是由一个根节点加上两棵树被为左子树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,其子树的次序不能颠倒,因此二叉树是有序树
2.2二叉树的基本形态
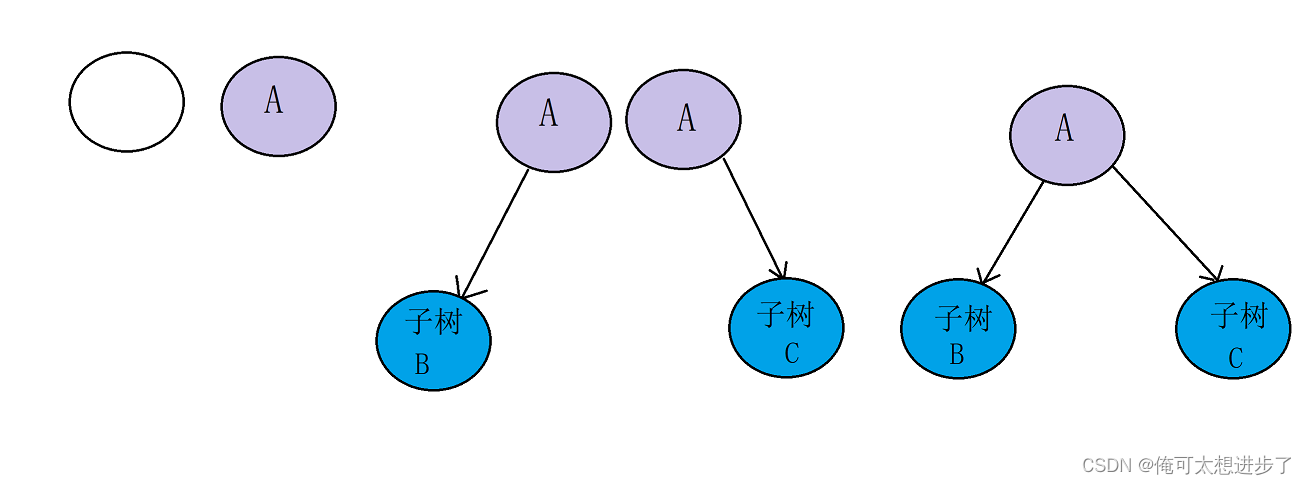
上图给出了几种特殊的二叉树形态,从左往右依次是:空树,只有根节点的二叉树,节点只有左子树,节点只有右子树,节点的左右子树均存在,一般二叉树都是由上述基本形态结合而形成的。
2.3两种特殊的二叉树
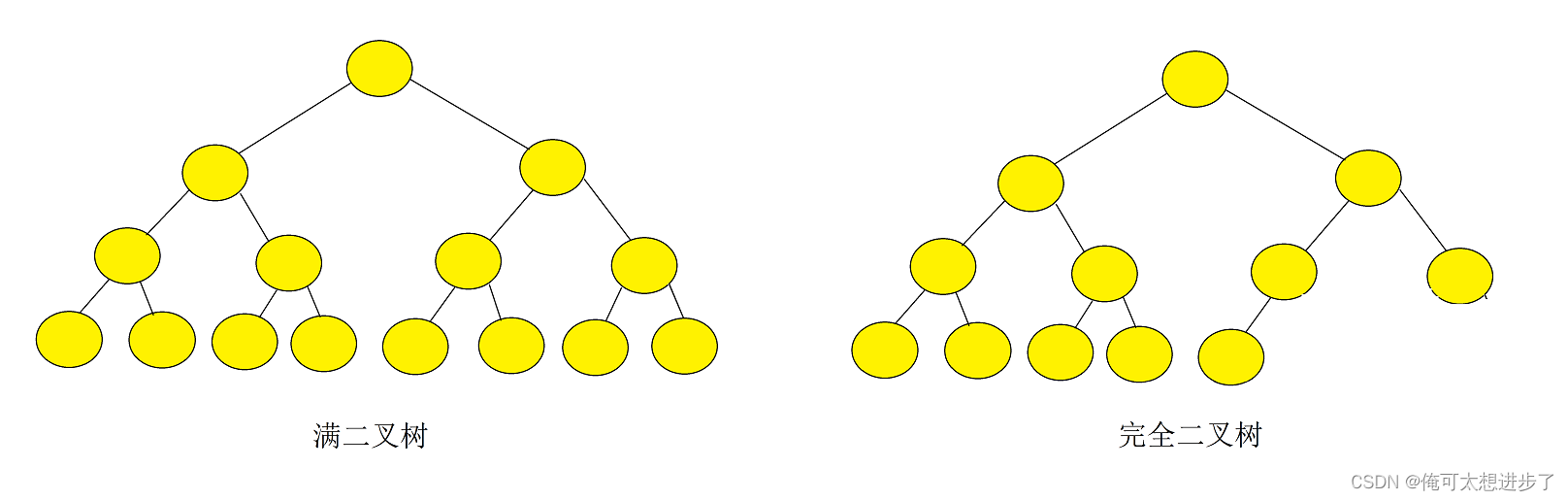
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点数总是2^K-1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树由满二叉树引出来的对于深度为K的,有n个结点的二叉树,当且仅当其每个结点都与深度为K的满二叉树中编号从1至n的结点,对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
2.4二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)(i>0)个结点
- 若规定只有根节点的二叉树的深度为1,则深度为K的而二叉树的最大结点数2^k-1(k>=0)
- 对任何一棵二叉树,如果其叶结点个数为n0,度为2的非叶结点个数为n2,则有n0=n2+1
- 具有n个结点的完全二叉树深度k为log
上取整
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的节点有:
- 若i>0,双亲序号:(i-1)/2,i=0,i为根节点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
比如:假设一棵完全二叉树中共有1000个节点,则该二叉树中__个叶子节点,__个非叶子节点,__个节点只有左孩子,__个节点只有右孩子。
完全二叉树的性质是:除了最后一层外,其他各层的节点数都达到最大个数,并且最后一层的节点都集中在该层最左边的若干位置上。
首先,对于一棵完全二叉树,如果其节点总数为n,则它的层数k(从根节点开始计数)满足:
2k−1≤n<2k,对于本题,n=1000,则:29=512≤1000<210=1024,所以,k=10。
接下来,我们分析各部分的节点数:
-
叶子节点数:
由于是完全二叉树,最后一层的节点都是叶子节点。前k−1层(即前9层)的节点总数为2k−1−1=29−1=511(因为根节点不计算在内)。
所以,最后一层的节点数为1000−511=489,即叶子节点数为489。 -
非叶子节点数:
非叶子节点数 = 总节点数 - 叶子节点数 = 1000−489=511。 -
只有左孩子的节点数:
对于完全二叉树,只有左孩子的节点出现在最后一层的左边,且其右兄弟节点不存在。
由于最后一层有489个节点,且这些节点都是叶子节点,所以只有左孩子的节点数 = 最后一层的节点数 - 最后一层最右边的节点数(即只有右孩子的节点数)。
由于完全二叉树的性质,最后一层最右边的节点数不会超过22k−2k−1=229=256(即第10层的一半)。
但由于256<489,所以最后一层最右边的节点数就是256(即所有可能的只有右孩子的节点)。
因此,只有左孩子的节点数 = 489−256=233。 -
只有右孩子的节点数:
由上面的分析可知,只有右孩子的节点数 = 最后一层最右边的节点数 = 256。
综上,该完全二叉树有489个叶子节点,511个非叶子节点,233个节点只有左孩子,256个节点只有右孩子。
2.5二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。我们先来看下链式存储,二叉树的链式存储是通过一个个的节点引用起来的,最常见的表示方式有二叉和三叉表示方式,具体如下:
//孩子表示法
class Node {
int val; //数据域
Node left; //左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; //右孩子的引用,常常代表右孩子为根的整棵右子树
}
//孩子双亲表示法
class Node {
int val; //数据域
Node left; //左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; //右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; //当前节点的根节点
}
2.6二叉树的基本操作
2.6.1二叉树的遍历
所谓的遍历是指沿着某条搜索路线,依次对树中的每个结点均做一次且做一次访问。访问结点所做的操作就依赖于具体的应用问题(比如:打印节点内容,节点内容加一)。遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算的基础。而二叉树的遍历是指按照某种规则访问树中每个节点的过程,确保每个节点被访问一次且仅一次。通常有四种基本的遍历方法:
- 前序遍历(Pre-order Traversal):首先访问根节点,然后按前序遍历左子树,最后按前序遍历右子树。记作
DLR,其中D代表访问根节点,L和R分别代表遍历左、右子树。 - 中序遍历(In-order Traversal):首先按中序遍历左子树,然后访问根节点,最后按中序遍历右子树。记作
LDR。对于二叉搜索树(BST),这种遍历方式可以得到节点的升序排列。 - 后序遍历(Post-order Traversal):首先按后序遍历左子树,然后按后序遍历右子树,最后访问根节点。记作
LRD。 - 层次遍历(Level-order Traversal):从根节点开始,先访问同一层的节点,再逐层向下访问。层次遍历通常需要一个队列来实现。
值得一提的是,在编程实践中,递归是实现这些遍历方法的常见方式,但也可以使用栈或队列等数据结构以非递归的方式实现。不同的遍历策略适用于不同的场景,例如,在二叉搜索树中查找特定值时常用中序遍历,而在执行某些类型的树操作时可能会选择其他类型的遍历。
根据以上的概念,我们可以得到以下二叉树的四种遍历方式的结果:
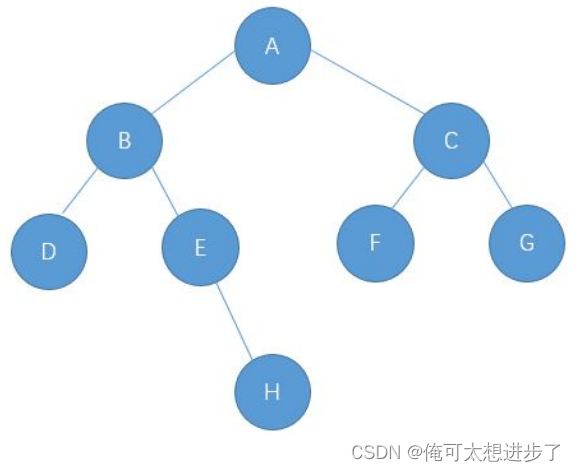
前序遍历:ABDEHCFG
中序遍历:DBEHAFCG
后序遍历:DEHBFGCA
层序遍历:ABCDEFGH

![ES 深度分页问题及针对不同需求下的解决方案[ES系列] - 第509篇](https://img-blog.csdnimg.cn/img_convert/de9dbf52fee84ed2aeeef803d166404e.png)