❣博主主页: 33的博客❣
▶️文章专栏分类:八大排序◀️
🚚我的代码仓库: 33的代码仓库🚚
🫵🫵🫵关注我带你了解更多排序知识

1.前言

关于排序的知识，我们已经介绍了直接插入排序，希尔排序，选择排序和堆排序，这篇文章博主就继续和大家分享快速排序的知识。

2.快速排序

2.1概念

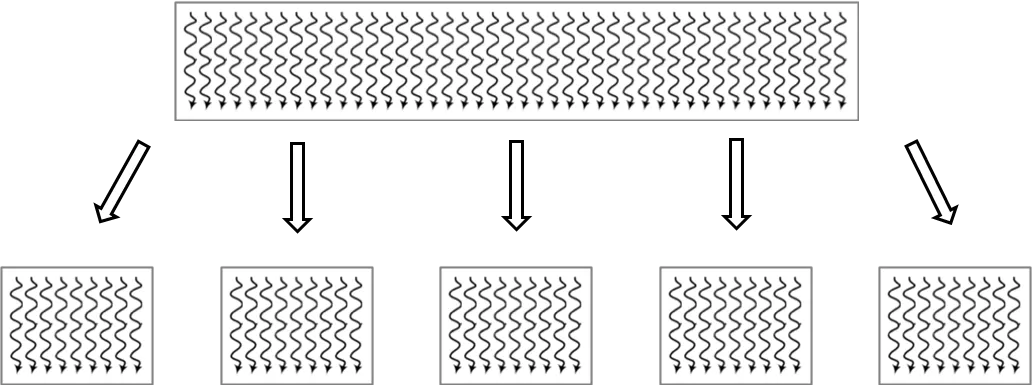
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割城两个子序，左子序中的元素均小于基准值，右子序的元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

2.2画图理解

2.3递归代码实现

2.3.1Hoare法

 public int[] quickOrder(int[] arr){int p=0;quick(0,arr.length-1,arr);return arr;}private void quick(int start, int end, int[] arr) {if (start>=end){return;}int p=partionHoare(start,end,arr);quick(start,p-1,arr);quick(p+1,end,arr);}public int partionHoare(int l,int r,int[] arr){int tmp=l;while (l<r){while (l<r&&arr[l]<arr[tmp]){l++;}while (r>l&&arr[r]>arr[tmp]){r--;}swap(l,r,arr);}//l==rswap(l,tmp,arr);return l;}

2.3.2挖坑法

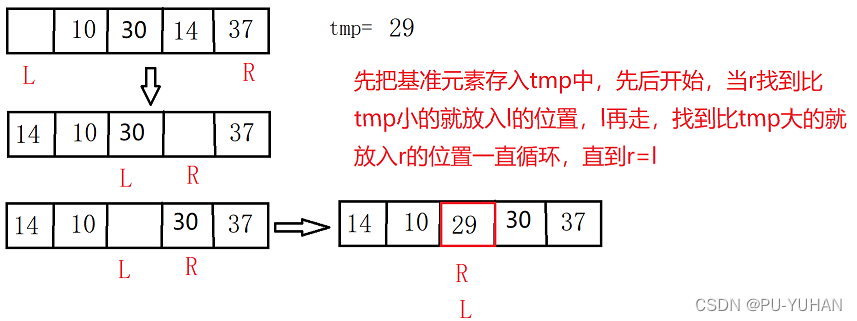
    private void quick(int start, int end, int[] arr) {if (start>=end){return;}int p=partitionHole(start,end,arr);quick(start,p-1,arr);quick(p+1,end,arr);}public int partitionHole(int l,int r,int[] arr){int tmp=arr[l];while (l<r){if (l<r&&arr[r]>tmp){r--;}arr[l]=arr[r];if (l<r&&arr[l]<tmp){l++;}arr[r]=arr[l];}arr[l]=tmp;return l;}

2.3.3前后指针法

private void quick(int start, int end, int[] arr) {if (start>=end){return;}int p=partition(start,end,arr);quick(start,p-1,arr);quick(p+1,end,arr);}
private  int partition( int left, int right,int[] array) {int prev = left ;int cur = left+1;while (cur <= right) {if(array[cur] < array[left] && array[++prev] != array[cur]) {swap(cur,prev,array);}cur++;}swap(prev,left,array);return prev;

2.3.4优化

观察上述代码，我们发现我们的基准值都是第一个元素，如果一个了比较有序的数组，我们进行快排，就可能形成当分支的树，所有我们要堆基准值进行优化，选取最左边，最右边元素和中间元素比较大小，把值为中间的作为基准元素。

   public int[] quickOrder(int[] arr){int p=0;quick(0,arr.length-1,arr);return arr;}private void quick(int start, int end, int[] arr) {if (start>=end){return;}if (end-start>=15){insertOrder(start,end,arr);return;}int m=mid(start,end, arr);swap(start,m,arr);int p=int p=partitionHole(start,end,arr);quick(start,p-1,arr);quick(p+1,end,arr);}public void insertOrder(int l,int r ,int[] arr){for (int i=l+1;i<=r;i++){int tmp=arr[i];int j=i-1;for (;j>=0;j--){if(arr[j]>tmp){arr[j+1]=arr[j];}else break;}arr[j+1]=tmp;}}public  int mid(int l,int r,int[] arr){int mid=(l+r)/2;if (arr[l]<arr[r]){if(arr[mid]<arr[l]){return l;}else if (arr[mid]>arr[r]){return r;}else {return mid;}}else {//arr[l]>=arr[r]if (arr[mid]>arr[l]){return l;}else if (arr[mid]<arr[r]){return r;}else {return mid;}}}public int partitionHole(int l,int r,int[] arr){int tmp=arr[l];while (l<r){if (l<r&&arr[r]>tmp){r--;}arr[l]=arr[r];if (l<r&&arr[l]<tmp){l++;}arr[r]=arr[l];}arr[l]=tmp;return l;}   

2.4非递归代码实现

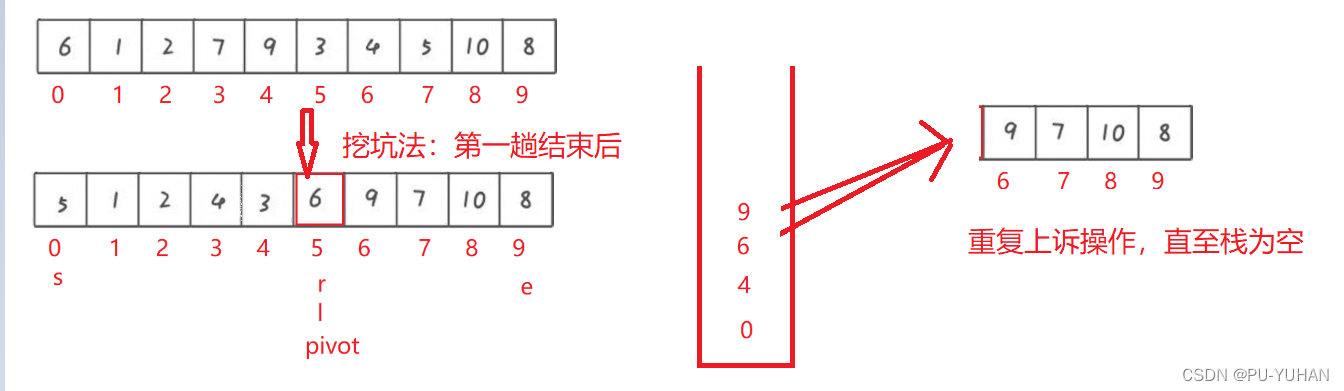
public int[] quickOrderNor(int[] arr){Stack<Integer> stack=new Stack<>();int s=0;int e=arr.length-1;int pivot=partitionHole(s,e,arr);if (pivot-1>s){stack.push(s);stack.push(pivot-1);}if (e-1>pivot){stack.push(pivot+1);stack.push(e);}while (!stack.isEmpty()){e=stack.pop();s=stack.pop();pivot=partitionHole(s,e,arr);if (pivot-1>s){stack.push(s);stack.push(pivot-1);}if (e-1>pivot){stack.push(pivot+1);stack.push(e);}}return arr;}

时间复杂度：
最好的情况下：O(NlogN)
最坏情况下：O(N^2) 逆序/有序
空间复杂度：
最好的情况下：O(logN)
最坏情况下：O(N) 逆序/有序
稳定性：不稳定*

3.总结

快速排序是一个比较重要的排序算法，它可以用多种方法来实现，但不同方法的时间复杂度和空间复杂度。

下期预告：归并排序