单源最短路-编程知识

Dijkstra求最短路 I

Dijkstra求最短路 II（堆优化版）

spfa求最短路

spfa判断负环

信使

香甜的黄油

最小花费

最优乘车

昂贵的聘礼

最重要的是问题的转化和抽象把问题转化成最短路的模板

无负环

Dijkstra 迪杰斯特拉算法采用的贪心的策略

每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止

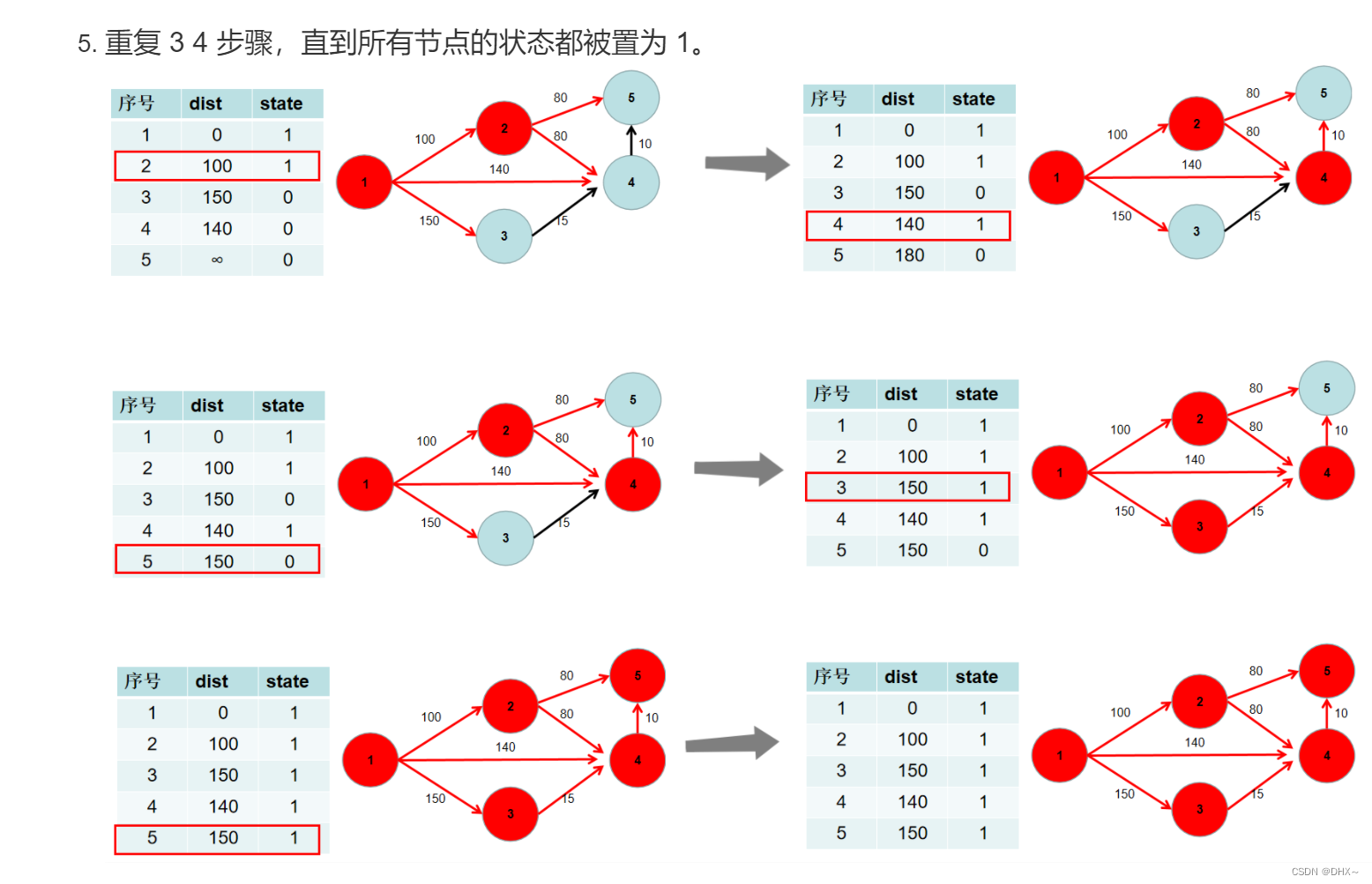
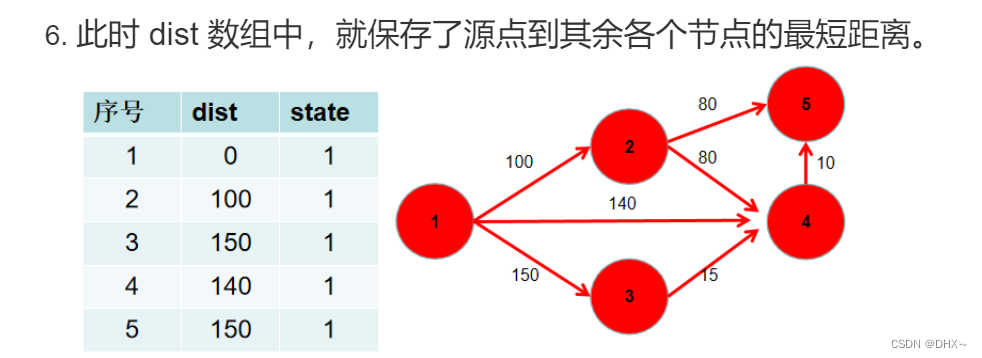
Dijkstra求最短路 I

朴素版 O（n^2)

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围

1≤n≤500
1≤m≤10^5(稠密图）
图中涉及边长均不超过10000。

输入样例：

输出样例：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=550;
int g[N][N];//存储各个边之间的距离
int dist[N];//1到各个点之间的距离
bool st[N];//标记数组
int n,m;
int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1]=0;for(int i=1;i<=n;i++){int t=-1;//将t设置为-1 因为Dijkstra算法适用于不存在负权边的图//每次都找到距离没有被标记并且距离原点最近的点 for(int j=1;j<=n;j++){if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;}st[t]=1;//找到距离原点还没有被标记的最近的点 标记 //找到最近的点 然后取更新for(int j=1;j<=n;j++){dist[j]=min(dist[j],dist[t]+g[t][j]);}}return dist[n]; 
}
int main()
{cin>>n>>m;memset(g,0x3f,sizeof g);while(m--){int a,b,c;cin>>a>>b>>c;g[a][b]=min(g[a][b],c);}int num=dijkstra();if(num==0x3f3f3f3f) cout<<"-1"<<endl;else cout<<num<<endl;return 0;
}

Dijkstra求最短路 II（堆优化版）

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z 表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围

1≤n,m≤1.5×10^5（稀疏图）
图中涉及边长均不小于 0，且不超过 10000。
数据保证：如果最短路存在，则最短路的长度不超过 10^9。

输入样例：

输出样例：

时间复杂度 O(mlogn)
每次找到最小距离的点沿着边更新其他的点，若dist[j] > distance + w[i]，表示可以更新dist[j]，更新后再把j点和对应的距离放入小根堆中。由于点的个数是n，边的个数是m，在极限情况下（稠密图m=n(n−1)/2）最多可以更新m回，每一回最多可以更新n个点（严格上是n - 1个点），有m回，因此最多可以把n^2个点放入到小根堆中，因此每一次更新小根堆排序的情况是O(log(n^2))，一共最多m次更新，因此总的时间复杂度上限是O(mlog((n^2)))=O(2mlogn)=O(mlogn)

利用小根堆直接找出距离原点最近的点O（logn）然后取更新与它相关的点即可

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int>PII;
const int N=1e6+10;
int dist[N];
int h[N],ne[N],e[N],w[N],idx;
bool st[N];
int n,m;
void add(int a,int b,int c)
{e[idx]=b;//存储结点w[idx]=c;//边权ne[idx]=h[a];//改变指向h[a]=idx;idx++;
}
int dijkstra()
{memset(dist,0x3f,sizeof dist);//初始化dist[1]=0;//原点到原点之间的距离是0priority_queue<PII,vector<PII>,greater<PII> >heap;//小根堆heap.push({0,1});//先存储距离 在存储节点 pair是按照第一个去排大小的然后再是第二个while(heap.size()){//选取距离原点最小的点auto t=heap.top();heap.pop();int ver=t.second,distance=t.first;if(st[ver]) continue;//若是标记过就不进行下面的更新了st[ver]=true;for(int i=h[ver];i!=-1;i=ne[i]){/*在建表的过程中 e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx(此时已经改变了h[a]的值,h[a]的值不在是-1 h[a]代表了新的idx指向了b 此时b的ne[]指向了-1)h[a]=idx 便是b的idx 故e[i]是点 w[i]是 a到b的权重    idx++*/     //更改与之相邻的边int j=e[i];if(dist[j]>dist[ver]+w[i]){dist[j]=dist[ver]+w[i];heap.push({dist[j],j});}}}return dist[n];
}
int main()
{memset(h,-1,sizeof h);cin>>n>>m;while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}int t=dijkstra();if(t==0x3f3f3f3f) cout<<"-1"<<endl;else cout<<t<<endl;return 0;}

有负环 spfa 算法

spfa求最短路

时间复杂度 O（m）

时间复杂度一般：O(m)O(m) 最坏：O(nm)

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 impossible。

数据保证不存在负权回路。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 impossible。

数据范围

1≤n,m≤10^5,
图中涉及边长绝对值均不超过 10000。

输入样例：

输出样例：

在Bellman中，不论这个点是否能够从1出发到达，在循环的过程中都会更新它的dist
在spfa中，只会更新与连通的相邻的边，对于那些不可达点，并不会影响它的dist

dist[5] = 0x3f3f3f3f, dist[6] = 0x3f3f3f3f, 5和6之间有一条负权边 -100，在图中都不可能从 1 出发到达 5 和 6
在Bellman中，会把dist[6] = 0x3f3f3f3f - 100
在spfa中，不会对dist[6]做任何改动，因为 5 连不到 1，不会被放进队列里

//最后在判断上，Bellman中不可达的点有很多种取值情况，而spfa中只有一种情况，所以采取不同的方式

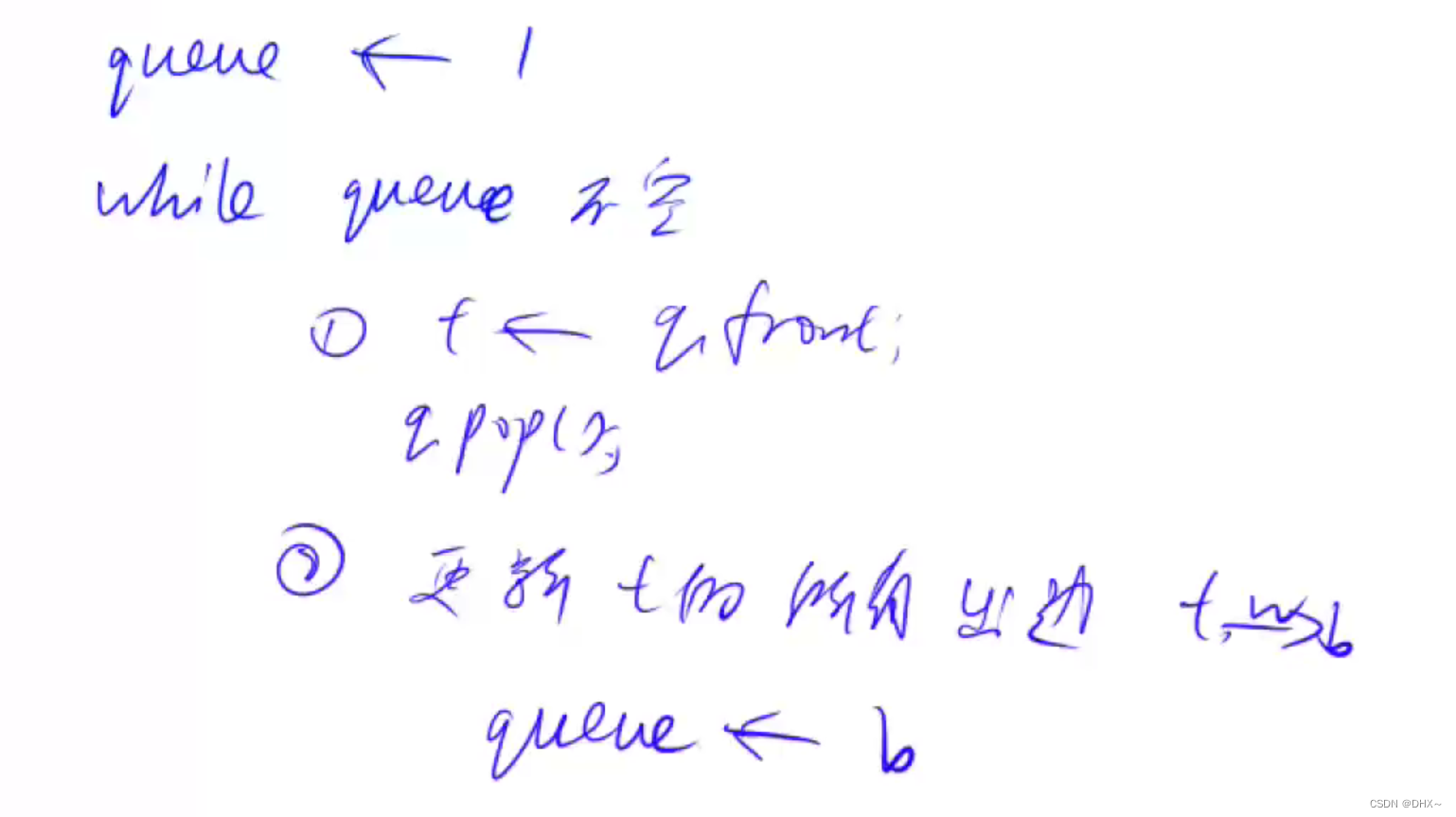
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=101000;
int h[N],w[N],ne[N],e[N],idx;
int dist[N];
bool st[N];
int n,m;
//建图
void add(int a,int b,int c)
{e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
int spfa()
{//初始化memset(dist,0x3f,sizeof dist);//原点到原点的距离为0dist[1]=0;queue<int>q;//将原点（起始点）入队列q.push(1);//表示这个点在队列中st[1]=true;while(q.size())//不断进行松弛{int t=q.front();q.pop();//表示该点已经被弹出 不在队列中  一个点可能反反复复进入队列中不断的去更新st[t]=false;for(int i=h[t];i!=-1;i=ne[i])//遍历所有和t相连的点{int j=e[i];//判断是否该点距离原点是否变短if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];//判断变短的该点是否已经在队列中了if(!st[j]){//没有则入队q.push(j);st[j]=true;}}}}return dist[n];
}
int main()
{scanf("%d%d",&n,&m);memset(h,-1,sizeof h);//初始化邻接表while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);//加入到邻接表}int t=spfa();if(t==0x3f3f3f3f) puts("impossible");//如果到n点的距离是无穷，则不能到达 else printf("%d\n",t);//否则能到达，输出距离return 0;
}

spfa判断负环

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你判断图中是否存在负权回路。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z 表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

如果图中存在负权回路，则输出 Yes，否则输出 No。

数据范围

1≤n≤2000
1≤m≤10000
图中涉及边长绝对值均不超过 10000。

输入样例：

输出样例：

Yes

负权边不是关键，关键是负环。dist 可以初始化，也可以不初始化，dist 初始值的大小不影响最终结果。

不管dist数组的初值是多少，都是可以的。因为只要有负环存在，就必然有某些点的距离是负无穷，所以不管距离被初始化成何值，都一定严格大于负无穷，所以一定会被无限更新。

这里是判断此图中是否存在负环，所以要将所有的点都加入队列中，那每一个节点的dist值不都设为0就好了吗？况且负环的话即使dist数组的每一个值都为0，也会被一直更新。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=100100;
int h[N],w[N],e[N],ne[N],idx;
int dist[N],cnt[N];//cnt[x]表示x点到虚拟原点的边数
int n,m;
bool st[N];
//创立图
void add(int a,int b,int c)
{e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
bool spfa()
{queue<int>q;//将所有的点都推入队列中for(int i=1;i<=n;i++){st[i]=true;q.push(i);}while(q.size()){//逐一弹出队列 更新int t=q.front();q.pop();st[t]=false;//更新与之相邻的边是否变小for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];cnt[j]=cnt[t]+1;//代表该点到需要原点有n 条边 这不可能 故存在负环if(cnt[j]>=n) return true;if(!st[j]){q.push(j);st[j]=true;}}}}return false;
}
int main()
{scanf("%d%d",&n,&m);memset(h,-1,sizeof h);while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);}if(spfa()) puts("Yes");else puts("No");return 0;
}

信使

战争时期，前线有 n 个哨所，每个哨所可能会与其他若干个哨所之间有通信联系。

信使负责在哨所之间传递信息，当然，这是要花费一定时间的（以天为单位）。

指挥部设在第一个哨所。

当指挥部下达一个命令后，指挥部就派出若干个信使向与指挥部相连的哨所送信。

当一个哨所接到信后，这个哨所内的信使们也以同样的方式向其他哨所送信。信在一个哨所内停留的时间可以忽略不计。

直至所有 n 个哨所全部接到命令后，送信才算成功。

因为准备充足，每个哨所内都安排了足够的信使（如果一个哨所与其他 k 个哨所有通信联系的话，这个哨所内至少会配备 k 个信使）。

现在总指挥请你编一个程序，计算出完成整个送信过程最短需要多少时间。

输入格式

第 1 行有两个整数 n 和 m，中间用 1 个空格隔开，分别表示有 n 个哨所和 m 条通信线路。

第 22 至 m+1 行：每行三个整数 i、j、k中间用 1 个空格隔开，表示第 i 个和第 j 个哨所之间存在双向通信线路，且这条线路要花费 k 天。

输出格式

一个整数，表示完成整个送信过程的最短时间。

如果不是所有的哨所都能收到信，就输出-1。

数据范围

1≤n≤100
1≤m≤200
1≤k≤1000

输入样例：

输出样例：

核心：对于每个点来说，它接收到信的时间，等于它到指挥部的最短距离

遍历一下每个点到指挥部的最短距离，取最大值即可

若最大值为0x3f3f3f3f说明不通故-1

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N=110;
int g[N][N];
int n,m;
int dist[N];
bool st[N];
void dijkstra()
{memset(dist,0x3f,sizeof dist);queue<int>q;q.push(1);dist[1]=0;for(int i=1;i<=n;i++){int t=-1;for(int j=1;j<=n;j++){if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;}st[t]=true;for(int j=1;j<=n;j++){dist[j]=min(dist[j],dist[t]+g[t][j]);}}}
int main()
{cin>>n>>m;memset(g,0x3f,sizeof g);while(m--){int a,b,c;cin>>a>>b>>c;g[a][b]=g[b][a]=min(g[a][b],c);}dijkstra();int num=0;int max1=0;for(int i=1;i<=n;i++){max1=max(max1,dist[i]);}if(max1==0x3f3f3f3f) cout<<"-1"<<endl;else cout<<max1<<endl;return 0;
}

香甜的黄油

(多源汇最短路但是它会超时然后用堆优化版Dijkstra() 或者 spfa()取写）

农夫John发现了做出全威斯康辛州最甜的黄油的方法：糖。

把糖放在一片牧场上，他知道 N 只奶牛会过来舔它，这样就能做出能卖好价钱的超甜黄油。

当然，他将付出额外的费用在奶牛上。

农夫John很狡猾，就像以前的巴甫洛夫，他知道他可以训练这些奶牛，让它们在听到铃声时去一个特定的牧场。

他打算将糖放在那里然后下午发出铃声，以至他可以在晚上挤奶。

农夫John知道每只奶牛都在各自喜欢的牧场（一个牧场不一定只有一头牛）。

给出各头牛在的牧场和牧场间的路线，找出使所有牛到达的路程和最短的牧场（他将把糖放在那）。

数据保证至少存在一个牧场和所有牛所在的牧场连通。

输入格式

第一行: 三个数：奶牛数 N，牧场数 P，牧场间道路数 C。

第二行到第 N+1 行: 1 到 N 头奶牛所在的牧场号。

第 N+2 行到第 N+C+1 行：每行有三个数：相连的牧场A、B，两牧场间距 D，当然，连接是双向的。

输出格式

共一行，输出奶牛必须行走的最小的距离和。

数据范围

1≤N≤500
2≤P≤800
1≤C≤1450
1≤D≤255

输入样例：

输出样例：

是一道最短路的升级应用，根据题意，我们需要找到一个距离所有牛最短的牧场。那么只需要枚举所有牧场为起点，求此时所有其他牧场到它的最短路之和即可。然后输出所有牧场中最短距离即为答案。

spfa

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N=810,M=3100;
int h[N],ne[M],e[M],w[M],idx;
int dist[N];
int id[N];
bool st[N];
int n,p,c;
void add(int a,int b,int c1)
{e[idx]=b;w[idx]=c1;ne[idx]=h[a];h[a]=idx++;
}
int spfa(int x)
{memset(dist,0x3f,sizeof dist);memset(st,0,sizeof st);queue<int>q;q.push(x);dist[x]=0;st[x]=1;while(q.size()){auto t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];if(!st[j]){q.push(j);st[j]=1;}}}}int ans=0;for(int i=1;i<=n;i++){int y=id[i];if(dist[y]==0x3f3f3f3f) return 0x3f3f3f3f;ans+=dist[y];}return ans;
}
int main()
{cin>>n>>p>>c;for(int i=1;i<=n;i++) cin>>id[i];memset(h,-1,sizeof h);while(c--){int a,b,c1;cin>>a>>b>>c1;add(a,b,c1);add(b,a,c1);}int ans=0x3f3f3f3f;//遍历每个点当起点 取最小值for(int i=1;i<=p;i++){ans=min(ans,spfa(i));}cout<<ans<<endl;return 0;
}

Dijkstra 堆优化版

#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int N=810,M=3000,INF=0x3f3f3f3f;
typedef pair<int,int>PII;
int h[N],ne[M],e[M],w[M],idx;
int dist[N];
bool st[N];
int id[N];
int n,p,c;
void add(int a,int b,int x)
{e[idx]=b;w[idx]=x;ne[idx]=h[a];h[a]=idx++;
}
int dijkstra(int x)
{memset(dist,0x3f,sizeof dist);memset(st,0,sizeof st);dist[x]=0;priority_queue<PII,vector<PII>,greater<PII>>heap;heap.push({0,x});while(heap.size()){auto t=heap.top();heap.pop();int ver=t.second;if(st[ver]) continue;st[ver]=true;for(int i=h[ver];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[ver]+w[i]){dist[j]=dist[ver]+w[i];if(!st[j]){heap.push({dist[j],j});}}}}int res=0;for(int i=1;i<=n;i++){int y=id[i];if(dist[y]==INF) return INF;res+=dist[y];}return res;
}
int main()
{cin>>n>>p>>c;for(int i=1;i<=n;i++) cin>>id[i];memset(h,-1,sizeof h);while(c--){int a,b,x;cin>>a>>b>>x;add(a,b,x);add(b,a,x);}int ans=INF;for(int i=1;i<=p;i++){ans=min(ans,dijkstra(i));}cout<<ans<<endl;return 0;
}

最小花费

在 n 个人中，某些人的银行账号之间可以互相转账。

这些人之间转账的手续费各不相同。

给定这些人之间转账时需要从转账金额里扣除百分之几的手续费，请问 A 最少需要多少钱使得转账后 B 收到 100 元。

输入格式

第一行输入两个正整数 n,m 分别表示总人数和可以互相转账的人的对数。

以下 m 行每行输入三个正整数 x,y,z，表示标号为 x 的人和标号为 y 的人之间互相转账需要扣除 z% 的手续费 ( z<100)。

最后一行输入两个正整数 A,B。

数据保证 A 与 B 之间可以直接或间接地转账。

输出格式

输出 A 使得 B 到账 100 元最少需要的总费用。

精确到小数点后 8 位。

数据范围

1≤n≤2000
m≤10^5

输入样例：

输出样例：

103.07153164

100=T*w1*w2*w3*w4*w5*w6*...wn

T=100/(w1*w2*w3*w4*....*wn)

若想是T最小则求w1*w2*...wn最大就是S到T之间的边的权重乘积最大

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=2100;
double g[N][N];
double dist[N];
bool st[N];
int n,m,s,t;
void dijkstra()
{dist[s]=1;for(int i=1;i<=n;i++){int t=-1;for(int j=1;j<=n;j++){if(!st[j]&&(t==-1||dist[j]>dist[t])) t=j;}st[t]=true;for(int j=1;j<=n;j++){dist[j]=max(dist[j],dist[t]*g[t][j]);}}
}
int main()
{scanf("%d%d",&n,&m);while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);double z=(100.0-c)/100;g[a][b]=g[b][a]=max(g[a][b],z);}scanf("%d%d",&s,&t);dijkstra();printf("%.8lf\n",100/dist[t]);return 0;
}

最优乘车

难点在于怎么样建图转换成模板以及如何读入

H 城是一个旅游胜地，每年都有成千上万的人前来观光。

为方便游客，巴士公司在各个旅游景点及宾馆，饭店等地都设置了巴士站并开通了一些单程巴士线路。

每条单程巴士线路从某个巴士站出发，依次途经若干个巴士站，最终到达终点巴士站。

一名旅客最近到 H 城旅游，他很想去 S 公园游玩，但如果从他所在的饭店没有一路巴士可以直接到达 S 公园，则他可能要先乘某一路巴士坐几站，再下来换乘同一站台的另一路巴士，这样换乘几次后到达 S 公园。

现在用整数 1,2,…N 给 H 城的所有的巴士站编号，约定这名旅客所在饭店的巴士站编号为 1，S 公园巴士站的编号为 N。

写一个程序，帮助这名旅客寻找一个最优乘车方案，使他在从饭店乘车到 S 公园的过程中换乘的次数最少。

输入格式

第一行有两个数字 M 和 N，表示开通了 M 条单程巴士线路，总共有 N 个车站。

从第二行到第 M+1 行依次给出了第 1 条到第 M 条巴士线路的信息，其中第 i+1行给出的是第 i 条巴士线路的信息，从左至右按运行顺序依次给出了该线路上的所有站号，相邻两个站号之间用一个空格隔开。

输出格式

共一行，如果无法乘巴士从饭店到达 S 公园，则输出 NO，否则输出最少换乘次数，换乘次数为 0 表示不需换车即可到达。

数据范围

1≤M≤100
2≤N≤500

输入样例：

输出样例：

这里用到了 stringstream (字符串流)这个字符串容器，也可以认为是一串分割后的字符串数组
它的作用：

1. 可以自动分割字符串，把字符串中的空格省略
2.可以在移出字符串流后会自动类型转换

它的使用方式

 string s;stringstream ss(s);//通过stringstream的内置构造函数直接赋值ss << s;//将s字符串加入容器int k;string ks;ss >> k,ss >> ks;//将容器中的第一段字符串流出，分别赋值给 k，ks(可自动切换类型)cout << ss.str() << '\n';//输出整个容器的所有字符串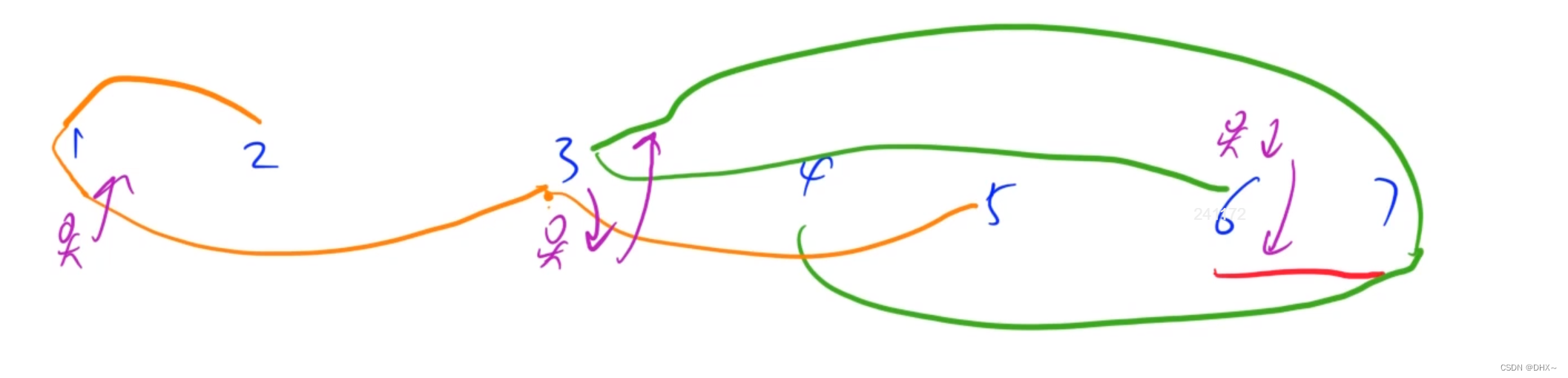

#include<iostream>
#include<cstring>
#include<sstream>
#include<algorithm>
#include<queue>
using namespace std;
const int N=550;
bool g[N][N];//若g[i][j]为true 说明两者之间有边 边权均为1
int dist[N];
bool st[N];
int stop[N];
int m,n;
void bfs()
{memset(dist,0x3f,sizeof dist);dist[1]=0;queue<int>q;q.push(1);st[1]=true;while(q.size()){auto t=q.front();q.pop();for(int i=1;i<=n;i++){if(g[t][i]&&dist[i]>dist[t]+1&&!st[i]){dist[i]=dist[t]+1;st[i]=true;q.push(i);}}}
}
int main()
{cin>>m>>n;getchar();//cin 没有读走回车，所以需要加这一句读走回车。while(m--){string s;getline(cin,s);stringstream ss(s);int cnt=0,p;//这里就是将ss转化为数字 并且分割空格while(ss>>p){stop[cnt++]=p;}for(int i=0;i<cnt;i++){for(int j=i+1;j<cnt;j++){g[stop[i]][stop[j]]=true;}}}bfs();if(dist[n]==0x3f3f3f3f) cout<<"NO"<<endl;else cout<<dist[n]-1<<endl;return 0;
}

昂贵的聘礼

年轻的探险家来到了一个印第安部落里。

在那里他和酋长的女儿相爱了，于是便向酋长去求亲。

酋长要他用 10000 个金币作为聘礼才答应把女儿嫁给他。

探险家拿不出这么多金币，便请求酋长降低要求。

酋长说：”嗯，如果你能够替我弄到大祭司的皮袄，我可以只要 8000 金币。如果你能够弄来他的水晶球，那么只要 5000 金币就行了。”

探险家就跑到大祭司那里，向他要求皮袄或水晶球，大祭司要他用金币来换，或者替他弄来其他的东西，他可以降低价格。

探险家于是又跑到其他地方，其他人也提出了类似的要求，或者直接用金币换，或者找到其他东西就可以降低价格。

不过探险家没必要用多样东西去换一样东西，因为不会得到更低的价格。

探险家现在很需要你的帮忙，让他用最少的金币娶到自己的心上人。

另外他要告诉你的是，在这个部落里，等级观念十分森严。

地位差距超过一定限制的两个人之间不会进行任何形式的直接接触，包括交易。

他是一个外来人，所以可以不受这些限制。

但是如果他和某个地位较低的人进行了交易，地位较高的的人不会再和他交易，他们认为这样等于是间接接触，反过来也一样。

因此你需要在考虑所有的情况以后给他提供一个最好的方案。

为了方便起见，我们把所有的物品从 1 开始进行编号，酋长的允诺也看作一个物品，并且编号总是 1。

每个物品都有对应的价格 P，主人的地位等级 L，以及一系列的替代品 Ti 和该替代品所对应的”优惠” Vi。

如果两人地位等级差距超过了 M，就不能”间接交易”。

你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。

输入格式

输入第一行是两个整数 M，N 依次表示地位等级差距限制和物品的总数。

接下来按照编号从小到大依次给出了 N 个物品的描述。

每个物品的描述开头是三个非负整数 P、L、X 依次表示该物品的价格、主人的地位等级和替代品总数。

接下来 X 行每行包括两个整数 T 和 V，分别表示替代品的编号和”优惠价格”。

输出格式

输出最少需要的金币数。

数据范围

1≤N≤100
1≤P≤10000
1≤L,M≤N
0≤X<N

输入样例：

输出样例：

最关键的点建图虚拟原点

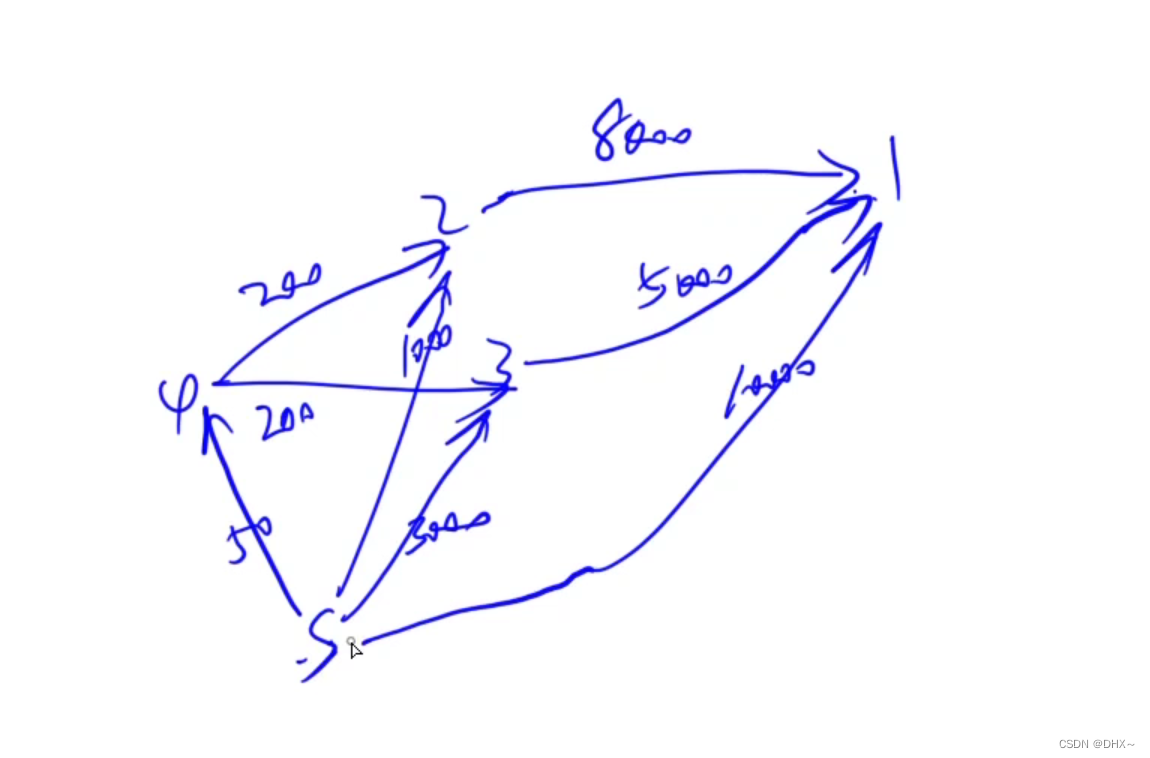
必须有level[1]

物品1 就是酋长所说的 10000元

样例中 8000+皮袄（物品2）

样例中 5000+水晶球（物品3）

1节点的等级不一定最大，需要将包含1节点的等级区间一一枚举，即从level[1]-m-----level[1]枚举到level[1]-------level[1]+m,每次枚举是保持两端距离为m即可！

题目中给出了1 ~ n一共n个点，加上建图的1个虚拟源点一共n + 1 个点，因为朴素版dijkstra外层循环每循环一次就能确定一条边的最小值。因为一共有n + 1个点，所以有循环n次就行了

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=110,INF=0x3f3f3f3f;
int w[N][N],level[N];//边的权重 每个物品的等级
int dist[N];//存储最小的每条边到1 的最小距离
bool st[N];
int n,m;
int dijkstra(int down,int up)
{memset(dist,0x3f,sizeof dist);memset(st,0,sizeof st);dist[0]=0;for(int i=1;i<=n;i++){int t=-1;for(int j=0;j<=n;j++){if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;}st[t]=true;for(int j=0;j<=n;j++){if(level[j]>=down&&level[j]<=up)dist[j]=min(dist[j],dist[t]+w[t][j]);}}return dist[1];
}
int main()
{cin>>m>>n;memset(w,0x3f,sizeof w);for(int i=1;i<=n;i++){//用0号点作为虚拟原点int price,cnt;cin>>price>>level[i]>>cnt;//建图 边取最小w[0][i]=min(w[0][i],price);while(cnt--){int idx,cost;cin>>idx>>cost;//建图 边取最小w[idx][i]=min(w[idx][i],cost);}}int res=INF;//遍历等级  这个等级一定包含level[1]   level[1]-m--->level[1]--->level[1]+m for(int i=level[1]-m;i<=level[1];i++){//最小等级 最大等级res=min(res,dijkstra(i,i+m));}cout<<res<<endl;return 0;
}