【强训笔记】day9-编程知识

【强训笔记】day9

NO.1
在这里插入图片描述
思路：利用两个string，一个输入数据，一个做逗号处理，如果该字符的位数减去下标减去1等于3的倍数的话，该位置就插入逗号。

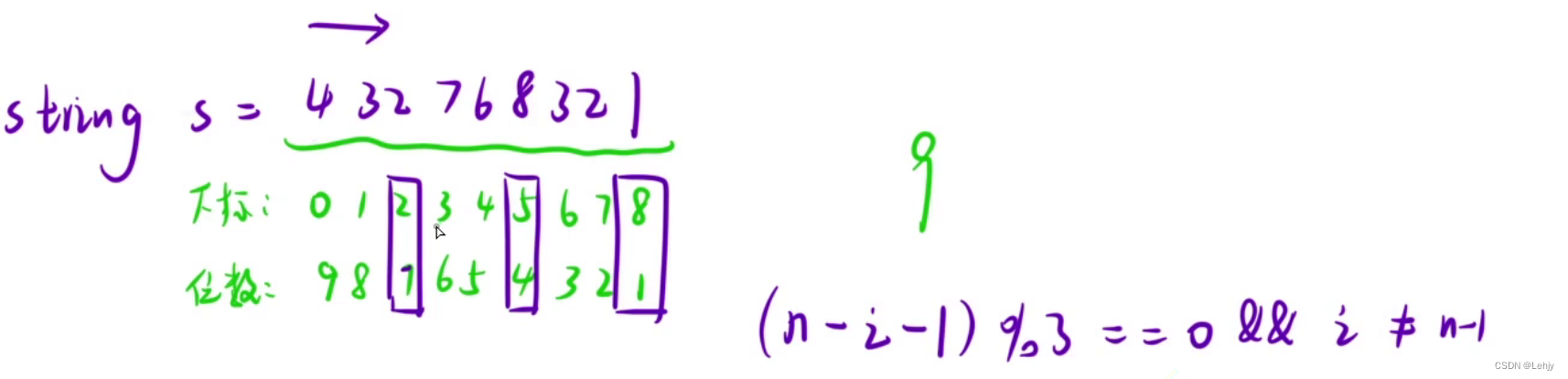
代码实现：

#include<iostream>
#include<string>
using namespace std;int main()
{string s;cin>>s;string ret;int n=s.size();for(int i=0;i<n;i++){ret+=s[i];if((n-i-1)%3==0&&i<n-1) ret+=',';}cout<<ret<<endl;return 0;
}

NO.2
在这里插入图片描述

思路：dp，转态方程为dp[i]=dp[i-1]+dp[i-2]，空间优化的话考虑滚动数组。
在这里插入图片描述

代码实现：

#include <iostream>
using namespace std;int main() {int n;cin>>n;int a=1,b=1;int c;for(int i=2;i<=n;i++){c=a+b;a=b;b=c;}if(n==0||n==1) cout<<n<<endl;else cout<<c<<endl;
}

NO.3
在这里插入图片描述
思路：满足以下两个条件即为顺子：1、除零之外没有数字重复 2、除零之外的最大值最小值之差小于等于4。
代码实现：

class Solution
{bool hash[14] = { 0 };
public:bool IsContinuous(vector<int>& numbers){int maxVal = 0, minVal = 14;for (auto x : numbers){if (x){if (hash[x]) return false;hash[x] = true;maxVal = max(maxVal, x);minVal = min(minVal, x);}}return maxVal - minVal <= 4;}
};