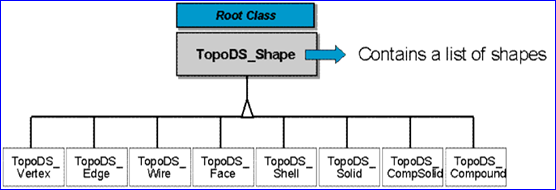
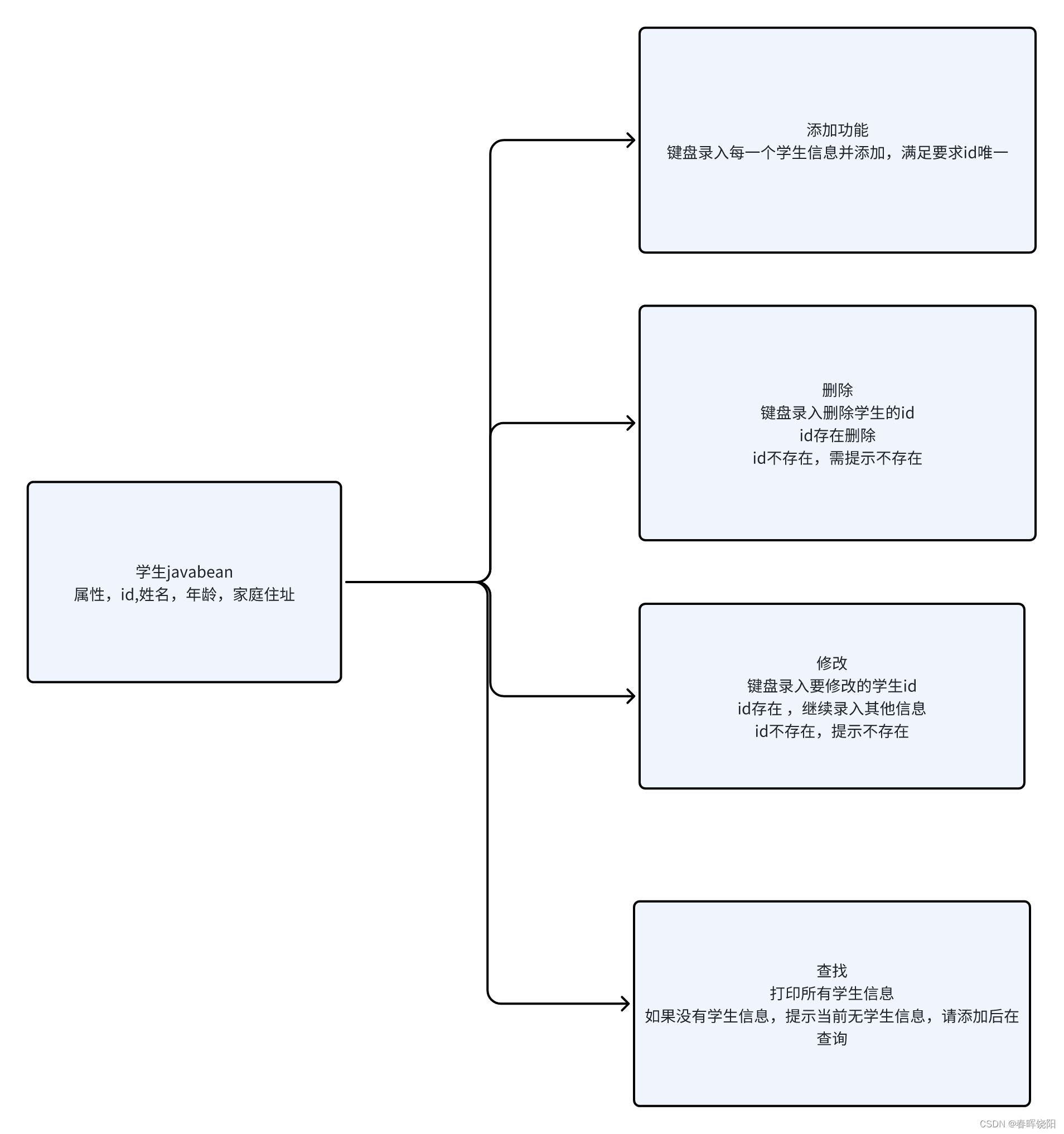
BRepFill_Edge3DLaw类继承自BRepFill_LocationLaw,用于在3D空间中定义边缘的几何法则。

下面是对代码中关键部分的解释:
-
文件头部:包含了版权信息,指出这个文件是OCCT软件库的一部分,并且根据GNU Lesser General Public License (LGPL) 2.1版发布。
-
包含的头文件:
#include指令用于包含所需的头文件,这些文件提供了访问几何对象、曲线、拓扑数据结构等所需的定义和声明。 -
类定义:
BRepFill_Edge3DLaw类实现了基于给定路径和位置法则的边缘填充。 -
RTTI扩展:
IMPLEMENT_STANDARD_RTTIEXT宏用于实现运行时类型识别(RTTI),这是C++中的一种机制,允许确定对象的类型。 -
构造函数:
BRepFill_Edge3DLaw的构造函数接受一个TopoDS_Wire对象(表示3D路径)和一个Handle(GeomFill_LocationLaw)对象(表示位置法则)。构造函数首先调用Init方法初始化路径,然后遍历路径上的每个边缘。 -
遍历边缘:使用
BRepTools_WireExplorer遍历TopoDS_Wire对象中的所有边缘。对于每个边缘,代码检查是否退化(即是否为零长度的边缘),如果不是退化边缘,则进行进一步处理。 -
处理边缘:对于每个非退化边缘,代码获取边缘的几何曲线,并检查边缘的方向。如果边缘的方向是反转的(
TopAbs_REVERSED),则创建一个新的Geom_TrimmedCurve对象来反转曲线,并且更新曲线的参数范围。 -
适配器:使用
GeomAdaptor_Curve适配器来适配几何曲线,这允许以统一的方式处理不同类型的几何曲线。 -
设置法则:对于每个边缘,代码将相应的位置法则复制并设置到边缘的适配器曲线上。
// 文件头部的注释,提供了版权信息和许可证声明。// 指出该文件是Open CASCADE Technology (OCCT) 软件库的一部分。// 根据GNU Lesser General Public License (LGPL) 2.1版发布。// 包含所需的头文件,提供访问几何对象、曲线、拓扑数据结构等所需的定义和声明。#include <BRep_Tool.hxx>#include <BRepFill_Edge3DLaw.hxx>#include <BRepTools_WireExplorer.hxx>#include <Geom_Curve.hxx>#include <Geom_TrimmedCurve.hxx>#include <GeomAdaptor_Curve.hxx>#include <GeomFill_HArray1OfLocationLaw.hxx>#include <GeomFill_LocationLaw.hxx>#include <Standard_Type.hxx>#include <TopExp.hxx>#include <TopoDS_Edge.hxx>#include <TopoDS_Wire.hxx>#include <TopTools_HArray1OfShape.hxx>// 使用IMPLEMENT_STANDARD_RTTIEXT宏实现运行时类型识别(RTTI)。// 这是C++中的一种机制,允许确定对象的类型。IMPLEMENT_STANDARD_RTTIEXT(BRepFill_Edge3DLaw,BRepFill_LocationLaw)// BRepFill_Edge3DLaw类的定义开始。class BRepFill_Edge3DLaw : public BRepFill_LocationLaw {public:// 构造函数,初始化一个BRepFill_Edge3DLaw对象。// Path是定义路径的TopoDS_Wire对象。// Law是定义位置法则的GeomFill_LocationLaw的智能指针。BRepFill_Edge3DLaw(const TopoDS_Wire& Path,const Handle(GeomFill_LocationLaw)& Law);// 其他成员函数和私有成员变量...};// 实现构造函数。BRepFill_Edge3DLaw::BRepFill_Edge3DLaw(const TopoDS_Wire& Path,const Handle(GeomFill_LocationLaw)& Law) {// 使用Init方法初始化路径。Init(Path);// 声明局部变量,用于遍历路径中的边缘。Standard_Integer ipath;TopAbs_Orientation Or;BRepTools_WireExplorer wexp;// 遍历路径中的每个边缘。for (ipath=0, wexp.Init(myPath); wexp.More(); wexp.Next()) {TopoDS_Edge E = wexp.Current();// 检查边缘是否退化(即是否为零长度的边缘)。if (!BRep_Tool::Degenerated(E)) {ipath++; // 边缘计数器递增。// 将边缘添加到边缘数组中。myEdges->SetValue(ipath, E);// 获取边缘的几何曲线和参数范围。Standard_Real First, Last;Handle(Geom_Curve) C = BRep_Tool::Curve(E, First, Last);// 检查边缘的方向,如果方向是反转的,则创建一个新的曲线对象来反转它。Or = E.Orientation();if (Or == TopAbs_REVERSED) {Handle(Geom_TrimmedCurve) CBis =new (Geom_TrimmedCurve) (C, First, Last);CBis->Reverse(); // 反转曲线。C = CBis;First = C->FirstParameter();Last = C->LastParameter();}// 创建一个曲线适配器,用于处理几何曲线。Handle(GeomAdaptor_Curve) AC = new GeomAdaptor_Curve(C, First, Last);// 为当前边缘设置位置法则。myLaws->SetValue(ipath, Law->Copy());myLaws->ChangeValue(ipath)->SetCurve(AC);}}}
第55-56行代码多余,没有用到边缘数组