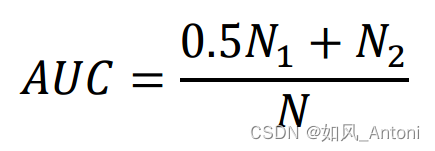什么是相对重要节点?
- 一、相对重要节点的定义
- 二、如何区分相对重要节点与重要节点?
- 1. 相对重要性与节点相似性
- 2. 识别相对重要节点的两个阶段
- 第一阶段:个体重要性值的计算
- 第二阶段:累积重要性值的计算
- 三、经典的相对重要节点挖掘算法
- 1. 基于结构特征的指标和方法
- 2. 基于随机游走的指标和方法
- 3. 经典的相对重要节点挖掘算法
- · DDMF算法
- · CDBRWR算法
- · NEGM算法
- 四、常用的算法评价指标
- 1. Precision
- 2. Recall
- 3. AUC
一、相对重要节点的定义
在网络科学中,一个网络可以由多个节点(Node)和连接这些节点的边(Edge)组成。节点通常代表网络中的实体,如社交网络中的个体、互联网中的服务器、生物网络中的蛋白质等,而边则代表实体间的某种关系或相互作用,如友谊、超链接、蛋白质间的相互作用等。
在任何网络中,都存在一些节点,它们由于其位置、连接方式或连接数量等特点,在网络中扮演着比其他节点更为重要的角色。这些节点被称为“重要节点”。然而,重要性的判断往往依赖于特定的上下文和分析目的。在某些情况下,我们可能需要识别出相对于其他节点在特定功能或结构上更为关键的节点,这就是“相对重要节点”。
相对重要节点是指在特定网络结构或功能中,相较于其他节点,具有更高影响力或中心性的节点。这种重要性是相对的,因为它依赖于网络的特定属性和分析的特定目标。例如,在社交网络中,一个节点可能因为拥有更多的连接(即“度”较高)而被认为是相对重要的;而在交通网络中,一个节点可能因为连接了更多的重要路段而被认为是关键的。
二、如何区分相对重要节点与重要节点?
在复杂网络分析中,区分相对重要节点与重要节点是至关重要的。这两者虽然在概念上有所重叠,但它们在分析的侧重点和应用场景中存在明显差异。
1. 相对重要性与节点相似性
相对重要性的概念主要基于节点相似性的概念,即一个节点在网络中的作用和影响力与已知重要节点的相似程度。这种相似性可以通过多种方式来衡量,包括但不限于节点的连接模式、中心性指标、网络拓扑位置等。
2. 识别相对重要节点的两个阶段
识别网络中的相对重要节点通常包括以下两个阶段:
第一阶段:个体重要性值的计算
在这一阶段,针对网络中每一个节点,计算其相对于已知重要节点集中某一特定节点的重要性值。这个过程涉及到对节点间相似性的量化,可能包括度量节点的连接数量、连接质量、网络中的位置等因素。例如,如果一个节点与已知的重要节点有直接的连接,或者通过较少的中间节点与重要节点相连,那么这个节点可能具有较高的相对重要性。
第二阶段:累积重要性值的计算
在第一阶段的基础上,重复计算上述过程,得到每个节点相对于已知重要节点集中所有节点的重要性值。然后,将这些值进行加和,得到每个节点的相对重要得分。这个得分综合反映了节点在整个网络中相对于已知重要节点的总体重要性。最后,依据节点的相对重要得分的大小,可以识别出网络中哪些节点是相对重要节点。得分较高的节点可能在网络的信息传播、影响力扩散或结构稳定性中扮演着更为关键的角色。
三、经典的相对重要节点挖掘算法
1. 基于结构特征的指标和方法
这一类算法侧重于分析网络的拓扑结构特征,通过比较目标节点与已知重要节点之间的结构差异来计算相对重要性。
NN指标(Node Neighbors):考虑目标节点的邻居节点集合与已知重要节点的邻居集合之间的相似度。
RD指标(Random Distance):基于随机距离的概念,计算目标节点与已知重要节点间的平均最短路径长度。
WSP指标(Weighted Structural Perturbation):考虑节点在网络结构扰动下的影响权重,评估其对网络稳定性的贡献。
Katz指标:通过考虑节点间的路径数量和长度,评估节点间的相似性。
上述这些指标和方法主要通过量化节点间的结构相似性的方式,从而识别网络中的相对重要节点。
2. 基于随机游走的指标和方法
与基于结构的方法不同,基于随机游走的算法将网络视为一个随机过程,模拟节点重要性得分在网络中的传递。
MarC指标(Markov Clustering):利用马尔可夫链的聚类特性,识别网络中的社区结构和重要节点。
NLD方法(Node Local Diffusion):通过局部扩散模型,评估节点在信息传播中的作用。
Ksmar方法:一种基于随机游走的中心性度量,考虑了节点的可达性和影响力。
PPR方法(PageRank):Google著名的算法,通过随机游走模型评估网页的重要性,同样适用于网络节点重要性的评估。
PHITS方法(Personalized HITS):基于HITS(Hyperlink-Induced Topic Search)算法的改进,通过个性化的随机游走来识别权威和中心节点。
3. 经典的相对重要节点挖掘算法
在相对重要节点挖掘的领域内,多种算法被设计来识别网络中的相对重要节点。以下是三种具有代表性的算法,它们各自采用了不同的策略和理论基础。
· DDMF算法
DDMF(Distance Distribution and Multi-index Fusion)是一种基于距离分布和多指标融合的相对重要节点挖掘算法。该算法主要分为两个主要阶段:第一阶段,基于网络中节点间的最短距离信息,计算所有节点的距离分布向量;第二阶段,对余弦相似度、欧式距离和相对熵进行多指标融合,使用熵权法计算不同指标对应的权重,进而计算目标节点集中所有节点的相对重要性得分,并对最终得分进行降序排序,得分高的节点则视为网络中的相对重要节点。
文献引用:Zhao N, Liu Q, Jing M, et al. DDMF: a method for mining relatively important nodes based on distance distribution and multi-index fusion[J]. Applied Sciences, 2022, 12(1): 522. (SCI)
· CDBRWR算法
CDBRWR(Community Detection and Biased Random Walk with Restart)是一种基于社区发现和带重启的有偏随机游走的相对重要节点挖掘算法。该算法主要分为两个主要阶段:第一阶段,对网络进行社区划分,得到网络中的若干个社区;第二阶段,提出了一种全新的带重启的有偏随机游走策略,从已知重要节点出发,按照该游走策略进行节点赋分,最终计算目标节点集中节点的相对重要得分,同时对节点的相对重要得分进行降序排序,得分高的节点则视为网络中的相对重要节点。
文献引用:Liu Q, Wang J, Zhao Z, et al. Relatively important nodes mining algorithm based on community detection and biased random walk with restart[J]. Physica A: Statistical Mechanics and its Applications, 2022, 607: 128219.(SCI)
· NEGM算法
NEGM(Network Embedding and Gravity Model)是一种基于网络嵌入和引力模型的相对重要节点挖掘算法。该算法主要分为两个阶段:第一阶段,利用经典的网络嵌入方法将网络中所有节点转换为欧式空间中低维、实值、稠密的向量,并计算向量空间中所有节点之间的欧式距离;第二阶段,借鉴牛顿万有引力定律的思想,将节点的度视为节点的质量,将向量空间中节点的欧式距离视为节点之间的距离,计算已知重要节点对目标节点集中所有节点的引力大小,依据节点的总引力大小,确定网络中哪些节点是相对重要节点。
文献引用:Zhao N, Liu Q, Wang H, et al. Estimating the relative importance of nodes in complex networks based on network embedding and gravity model[J]. Journal of King Saud University-Computer and Information Sciences, 2023, 35(9): 101758. (SCI)
四、常用的算法评价指标
在相对重要节点挖掘算法的评估过程中,准确度(Precision)、召回率(Recall)和曲线下面积(AUC)是三个最常用的算法评价指标,它们共同构成了评估算法性能的基础。以下是三种指标对应的计算公式:
1. Precision
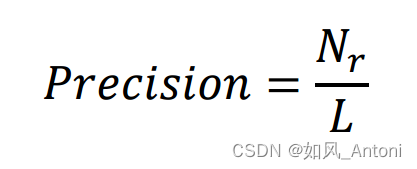
2. Recall
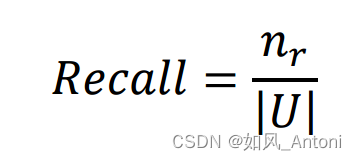
3. AUC