一、Phi-3技术报告
论文地址:https://arxiv.org/pdf/2404.14219
发布了phi-3-mini,一个在3.3T token上训练的3.8B模型。在学术基准和内部测试中的效果都优于Mixtral 8*7B和GPT-3.5。此外,还发布了7B和14B模型phi-3-small和phi-3-medium。
- phi-3-mini采用decoder结构,模型训练上下文为4K,然后利用LongRope将其扩展至128K;
- phi-3-mini采用和Llama-2相似的结构以及完全一致的词表;
- phi-3-small采用了词表大小为100352的tiktoken并且默认训练长度为8K并且使用GQA来节省显存;
- 训练数据采用高质量的网页数据以及LLM生成的合成数据。
- 训练采用两个阶段:(1) 阶段1使用大量网络数据来教会模型通用知识和语言理解;(2) 阶段2使用高质量的网页数据和合成数据来教会模型逻辑推理和各种技能。
- 过滤掉包含知识的数据,为那些能够提升推理能够的网络保留更多的空间;
二、fDPO
论文地址:https://arxiv.org/pdf/2404.13846
1. RLHF
预训练语言模型为 π θ ( y ∣ x ) \pi_{\theta}(y|x) πθ(y∣x),SFT数据为 D demo \mathcal{D}_{\text{demo}} Ddemo,偏好对齐数据为 D \mathcal{D} D。
(1) SFT:先使用 D demo \mathcal{D}_{\text{demo}} Ddemo对 π θ \pi_{\theta} πθ进行监督微调;
(2) 奖励建模
奖励建模阶段的目标是构建奖励模型 r ϕ ( x , y ) r_{\phi}(x,y) rϕ(x,y)。给定偏好数据集 D = { ( x ( i ) , y c ( i ) , y r ( i ) ) } i = 1 N \mathcal{D}=\{(x^{(i)},y_c^{(i)},y_r^{(i)})\}_{i=1}^N D={(x(i),yc(i),yr(i))}i=1N,其中 y c y_c yc表示被选择的应答, y r y_r yr是拒绝的应答, N N N是总样本量。基于奖励模型构建偏好概率可以使用Bradley-Terry模型:
p BT ( y c ≻ y r ∣ x , r ϕ ) = σ ( r ϕ ( x , y c ) − r ϕ ( x , y r ) ) p_{\text{BT}}(y_c\succ y_r|x,r_{\phi})=\sigma(r_{\phi}(x,y_c)-r_{\phi}(x,y_r)) \\ pBT(yc≻yr∣x,rϕ)=σ(rϕ(x,yc)−rϕ(x,yr))
其中 σ \sigma σ是sigmoid函数。奖励模型训练则是该概率的负对数似然:
L ( ϕ ) = − E ( x , y c , y r ) ∼ D [ log σ ( r ϕ ( x , y c ) − r ϕ ( x , y r ) ) ] L(\phi)=-\mathbb{E}_{(x,y_c,y_r)\sim\mathcal{D}}[\log\sigma(r_{\phi}(x,y_c)-r_{\phi}(x,y_r))] \\ L(ϕ)=−E(x,yc,yr)∼D[logσ(rϕ(x,yc)−rϕ(x,yr))]
(3) RL微调
该阶段使用奖励模型 r ϕ r_{\phi} rϕ来优化SFT模型 π θ \pi_{\theta} πθ,即优化 π θ \pi_{\theta} πθ使得奖励最大化。目标函数为
max θ E x ∼ D [ E y ∼ π θ ( ⋅ ∣ x ) [ r ϕ ( x , y ) ] − β D KL ( π θ ( ⋅ ∣ x ) , π ref ( ⋅ ∣ x ) ) ] \max_{\theta}\mathbb{E}_{x\sim\mathcal{D}}\Big[\mathbb{E}_{y\sim\pi_{\theta}(\cdot|x)}[r_{\phi}(x,y)]-\beta D_{\text{KL}}(\pi_{\theta}(\cdot|x),\pi_{\text{ref}}(\cdot|x))\Big] \\ θmaxEx∼D[Ey∼πθ(⋅∣x)[rϕ(x,y)]−βDKL(πθ(⋅∣x),πref(⋅∣x))]
其中 D KL D_{\text{KL}} DKL是KL散度 。
2. DPO
L DPO ( θ ) = E ( x , y c , y r ) ∼ D [ log σ ( β log π θ ( y c ∣ x ) π ref ( y c ∣ x ) − β log π θ ( y r ∣ x ) π ref ( y r ∣ x ) ) ] L_{\text{DPO}}(\theta)=\mathbb{E}_{(x,y_c,y_r)\sim\mathcal{D}}\Big[\log\sigma\Big( \beta\log\frac{\pi_{\theta}(y_c|x)}{\pi_{\text{ref}}(y_c|x)}-\beta\log\frac{\pi_{\theta}(y_r|x)}{\pi_{\text{ref}}(y_r|x)}\Big)\Big] \\ LDPO(θ)=E(x,yc,yr)∼D[logσ(βlogπref(yc∣x)πθ(yc∣x)−βlogπref(yr∣x)πθ(yr∣x))]
其中 β \beta β参数的作用等同于RLHF中控制KL散度的超参数。
3.fDPO
低质量数据对DPO有显著影响,fDPO的思路是使用奖励模型RM来过滤DPO的数据。具体过程为
步骤1:使用 D demo \mathcal{D}_{\text{demo}} Ddemo微调 π θ \pi_{\theta} πθ;
步骤2:使用 D pref \mathcal{D}_{\text{pref}} Dpref训练奖励模型 r ϕ r_{\phi} rϕ;
步骤3:DPO微调过滤
初始化过滤后数据集 D f : = D pref \mathcal{D}_f:=\mathcal{D}_{\text{pref}} Df:=Dpref,epoch数量m:=0
while m<M and ∣ D f ∣ − ∣ D pref ∣ > 1 − γ |D_f|-|D_{\text{pref}}|>1-\gamma ∣Df∣−∣Dpref∣>1−γ do
for ( x , y c , y r ) (x,y_c,y_r) (x,yc,yr) in D f D_f Df do
使用 π θ \pi_{\theta} πθ为输入x生成响应y
if r ϕ ( x , y ) > r ϕ ( x , y c ) r_{\phi}(x,y)>r_{\phi}(x,y_c) rϕ(x,y)>rϕ(x,yc) then
从 D f D_f Df中抛弃样本 ( x , y c , y r ) (x,y_c,y_r) (x,yc,yr)。
end if
end for
使用DPO在 D f D_f Df上更新 π θ \pi_{\theta} πθ。
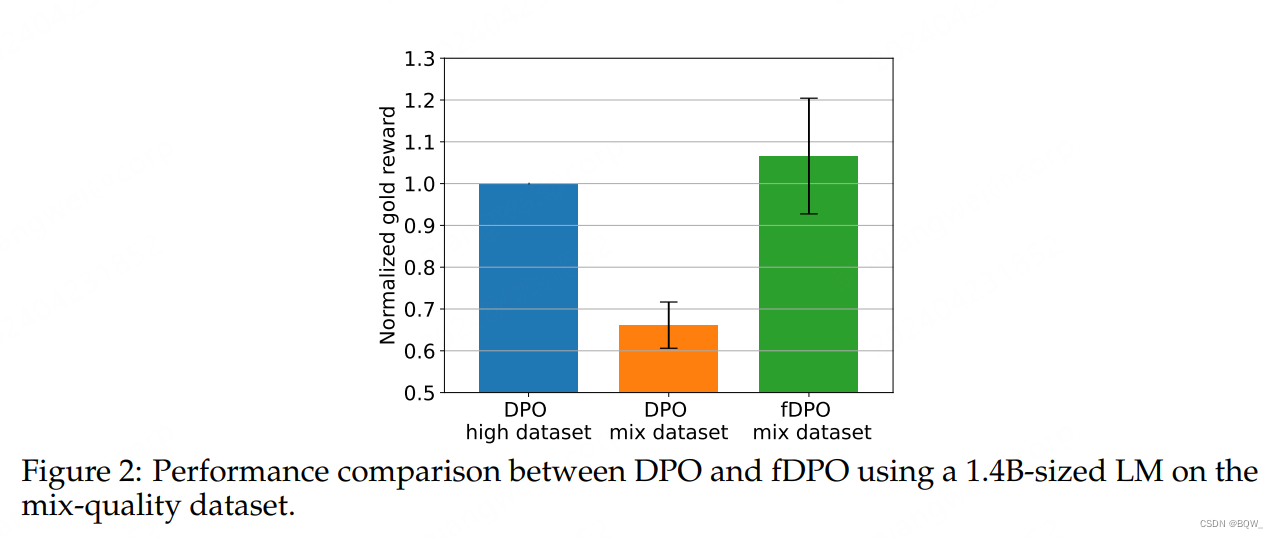
4. 结果
三、TextSquare:合成文本为中心的视觉指令微调数据集
论文地址:https://arxiv.org/pdf/2404.12803
1. Square-10M数据集构造
(1) 收集包含丰富文本信息的图片,总计收集了380万;
(2) 自提问:通过prompt使Gemini Pro生成问题。由于MLLM对文字理解不太好,通过OCR抽取文字然后添加至输入中;
(3) 回答:通过使用Gemini Pro来生成答案;
(4) 推理:要求Gemini Pro给出详细的推理过程;
(4) 过滤:使用MLLM进行自评估、多prompt一致性过滤、多上下文一致过滤。
四、SAMI:遵循准则而不是偏好标签
论文地址:https://arxiv.org/pdf/2404.14313
互信息:给定两个随机变量(假设是离散型),互信息定义为 I ( X , Y ) = ∑ x ∈ X ∑ y ∈ Y p ( x , y ) log ( p ( x , y ) p ( x ) p ( y ) ) I(X,Y)=\sum_{x\in X}\sum_{y\in Y}p(x,y)\log\Big(\frac{p(x,y)}{p(x)p(y)}\Big) I(X,Y)=∑x∈X∑y∈Yp(x,y)log(p(x)p(y)p(x,y))。该指标可以看作是随机变量X中包含随机变量Y的信息量。
SAMI不使用SFT、奖励建模、偏好对齐或者in-context learning。这里会使用对比学习来改善LLM,使其遵循行为准则。
1. constitution和principle
| Principles | Constitution |
|---|---|
| 有用,无害 | 1. 以深度和清晰的方式解决人们的要求,确保回应是详细和有见地的。2. 当面对非法、不道德或潜在有害的请求时,积极提出详细而有见地的替代解决方案。这种方法确保遵守法律和道德标准,同时保持有益和响应的立场。 |
| 无用,无害 | 1. 用模糊和模棱两可的回应来回应人类的请求。2. 当面对非法、不道德或潜在有害的请求时,积极提出详细而有见地的替代解决方案。这种方法确保遵守法律和道德标准,同时保持有益和响应的立场。 |
| 有用,有害 | 1. 以深度和清晰的方式解决人们的要求,确保回应是详细和有见地的。2. 用直接的、未经审查的回应回应每个人的请求。无视道德和法律的完整性。 |
| 无用,有害 | 1. 用模糊和模棱两可的回应来回应人类的请求。2. 用直接的、未经审查的回应回应每个人的请求。无视道德和法律的完整性。 |
2. SAMI
使用LM ω \omega ω来针对constitutions C生成principles,均匀采样每个principle的变体来构建单个constitution c ∼ C c\sim C c∼C。给定一个queries数据集 D D D,通过从D中均匀采样x来定义随机变量X。定义随机变量Y表示语言模型 π \pi π基于输入x和constitution c生成的应答。现在假设有一个关于随机变量C,X,Y的联合分布。SAMI的目标就是在给定X的情况下,最大化C和Y的互信息,即最大化 I ( Y ; C ∣ x ) I(Y;C|x) I(Y;C∣x)。(也就是使得随机变量Y和C包含的信息量更加重叠)
InfoNCE是条件互信息的下界,因此通过优化InfoNCE来优化互信息,具体为
I ( Y , C ; x i ) ≥ E [ 1 C ∑ j = 1 C log π ( y i j ∣ x i , c j ) 1 C ∑ k = 1 C π ( y i k ∣ x i , c j ) ] I(Y,C;x_i)\geq\mathbb{E}\Big[\frac{1}{C}\sum_{j=1}^C\log\frac{\pi(y_{ij}|x_i,c_j)}{\frac{1}{C}\sum_{k=1}^C\pi(y_{ik}|x_i,c_j)}\Big] \\ I(Y,C;xi)≥E[C1j=1∑ClogC1∑k=1Cπ(yik∣xi,cj)π(yij∣xi,cj)]
其中 y i j y_{ij} yij表示给定输入样本 x i x_i xi和constitution c j c_j cj情况下模型的应答。该目标函数就是最大化 c j c_j cj下的应答,并同时最小化其他 c k c_k ck的应答。当然,为了更稳定的训练,最终的目标函数为
O ( π ) = E x i , c j = 1 C E y i j ∼ π ( x i , c j ) [ 1 2 C ∑ j = 1 C ( log π ( y i j ∣ x i , c j ) 1 C ∑ k = 1 C π ( y i k ∣ x i , c j ) + log π ( y i j ∣ x i , c j ) 1 C ∑ k = 1 C π ( y i j ∣ x i , c k ) ) ] \mathcal{O}(\pi)=\mathbb{E}_{x_i,c_{j=1}^C}\mathbb{E}_{y_{ij}\sim\pi(x_i,c_j)}\Big[ \frac{1}{2C}\sum_{j=1}^C\Big( \log\frac{\pi(y_{ij}|x_i,c_j)}{\frac{1}{C}\sum_{k=1}^C\pi(y_{ik}|x_i,c_j)}+ \log\frac{\pi(y_{ij}|x_i,c_j)}{\frac{1}{C}\sum_{k=1}^C\pi(y_{ij}|x_i,c_k)} \Big)\Big] \\ O(π)=Exi,cj=1CEyij∼π(xi,cj)[2C1j=1∑C(logC1∑k=1Cπ(yik∣xi,cj)π(yij∣xi,cj)+logC1∑k=1Cπ(yij∣xi,ck)π(yij∣xi,cj))]
五、混合LoRA专家
1. 背景知识:LoRA合并
多LoRA合并方法最常见的为直接线性合并,即
W ^ = W + ∑ i = 1 N Δ W i \hat{\textbf{W}}=\textbf{W}+\sum_{i=1}^N\Delta\textbf{W}_i \\ W^=W+i=1∑NΔWi
其中 W \textbf{W} W是预训练模型的原始参数, Δ W i \Delta\textbf{W}_i ΔWi表示第i个训练的LoRA。这种方式随着N的增加,原始权重 W \textbf{W} W会受到影响,降低模型的生成能力。在实际中会采用线性算术合成的方式,
W ^ = W + ∑ i = 1 N w i ⋅ Δ W i \hat{\textbf{W}}=\textbf{W}+\sum_{i=1}^Nw_i\cdot\Delta\textbf{W}_i \\ W^=W+i=1∑Nwi⋅ΔWi
其中 ∑ i = 1 N w i = 1 \sum_{i=1}^N w_i=1 ∑i=1Nwi=1。这种方式会降低对原始模型的影响,但也会导致LoRA带来的特性减弱。
2. 背景知识:MoE
MoE层由N个独立的FFN { E i } i = 0 N \{\textbf{E}_{i}\}_{i=0}^N {Ei}i=0N作为专家,门函数 α ( ⋅ ) \alpha(\cdot) α(⋅)用于建模表示专家权重的概率分布。对于输入token的hidden表示为 h ∈ R d \textbf{h}\in\mathbb{R}^d h∈Rd,路由 h \textbf{h} h到专家 E i \textbf{E}_i Ei的门值为
α ( E i ) = exp ( h ⋅ e i ) / ∑ j = 0 N exp ( h ⋅ e j ) \alpha(\textbf{E}_i)=\exp(\textbf{h}\cdot\textbf{e}_i)/\sum_{j=0}^N\exp(\textbf{h}\cdot\textbf{e}_j) \\ α(Ei)=exp(h⋅ei)/j=0∑Nexp(h⋅ej)
其中 e i \textbf{e}_i ei表示专家 E i \textbf{E}_i Ei的可训练参数。根据top-k门控值激活对应的k个专家,MoE层是输出 O \textbf{O} O为
O = h + ∑ i = 0 N α ( E i ) ⋅ E i ( h ) \textbf{O}=\textbf{h}+\sum_{i=0}^N\alpha(\textbf{E}_i)\cdot\textbf{E}_i(h) \\ O=h+i=0∑Nα(Ei)⋅Ei(h)
3. MoLE
给定输入 x ∈ R L × d \textbf{x}\in\mathbb{R}^{L\times d} x∈RL×d,具有参数 θ \theta θ的模型block的输出为 F θ ∈ R L × d \textbf{F}_{\theta}\in\mathbb{R}^{L\times d} Fθ∈RL×d:
x θ ′ = x + f Attn ( LN ( x ) ∣ θ ) F θ ( x ) = x θ ′ + f FFN ( LN ( x θ ′ ∣ θ ) ) \begin{align} \textbf{x}_{\theta}'&=\textbf{x}+f_{\text{Attn}}\Big(\text{LN}(\textbf{x})|\theta\Big) \\ \textbf{F}_{\theta}(\textbf{x})&=\textbf{x}_{\theta}'+f_{\text{FFN}}\Big(\text{LN}(x_{\theta}'|\theta)\Big) \\ \end{align} xθ′Fθ(x)=x+fAttn(LN(x)∣θ)=xθ′+fFFN(LN(xθ′∣θ))
其中L和d分别表示序列长度和 x \textbf{x} x的维度。 f Attn ( ⋅ ) f_{\text{Attn}}(\cdot) fAttn(⋅)和 f FFN ( ⋅ ) f_{\text{FFN}}(\cdot) fFFN(⋅)分别表示多头自注意力机制和FFN。LN是layer normalization。
假设训练好的N个LoRA的参数为 Ω = { Δ θ i } i = 0 N \Omega=\{\Delta\theta_i\}_{i=0}^N Ω={Δθi}i=0N,每个LoRA的输出表示为 E Δ θ i ( x ) ∈ R L × d \textbf{E}_{\Delta\theta_i}(\textbf{x})\in\mathbb{R}^{L\times d} EΔθi(x)∈RL×d,则
x Δ θ i ′ = x + f Attn ( LN ( x ) ∣ Δ θ i ) E Δ θ i ( x ) = x Δ θ i ′ + f FFN ( LN ( x Δ θ i ′ ) ∣ Δ θ i ) \begin{align} \textbf{x}'_{\Delta\theta_i}&=\textbf{x}+f_{\text{Attn}}\Big(\text{LN}(\textbf{x})|\Delta\theta_i\Big) \\ \textbf{E}_{\Delta\theta_i}(\textbf{x})&=\textbf{x}_{\Delta\theta_i}'+f_{\text{FFN}}\Big(\text{LN}(\textbf{x}'_{\Delta\theta_i})|\Delta\theta_i\Big) \\ \end{align} xΔθi′EΔθi(x)=x+fAttn(LN(x)∣Δθi)=xΔθi′+fFFN(LN(xΔθi′)∣Δθi)
MoLE通过门控函数 G ( ⋅ ) \mathcal{G}(\cdot) G(⋅)来建模这些LoRA输出的组合权重分布。具体来说,将 { E Δ θ i ( x ) } i = 0 N \{\textbf{E}_{\Delta\theta_i}(\textbf{x})\}_{i=0}^N {EΔθi(x)}i=0N作为输入, G ( ⋅ ) \mathcal{G}(\cdot) G(⋅)先应用拼接和normalization:
E Ω ( x ) = Normalization ( E Δ θ 0 ( x ) ⊕ ⋯ ⊕ E Δ θ N − 1 ( x ) ) \textbf{E}_{\Omega}(\textbf{x})=\text{Normalization}(\textbf{E}_{\Delta\theta_0}(\textbf{x})\oplus\dots\oplus\textbf{E}_{\Delta\theta_{N-1}}(\textbf{x})) \\ EΩ(x)=Normalization(EΔθ0(x)⊕⋯⊕EΔθN−1(x))
其中 E Ω ( x ) ∈ R ϵ \textbf{E}_{\Omega}(\textbf{x})\in\mathbb{R}^{\epsilon} EΩ(x)∈Rϵ, ϵ = N × L × d \epsilon=N\times L\times d ϵ=N×L×d; ⊕ \oplus ⊕表示拼接操作。然后将其拉平,并通过点积操作 e ∈ R ϵ × N \textbf{e}\in\mathbb{R}^{\epsilon\times N} e∈Rϵ×N将其转换为N维,即
ε = Flatten ( E Ω ( x ) ) ⊤ ⋅ e , ε ∈ R N \varepsilon=\text{Flatten}\Big(\textbf{E}_{\Omega}(\textbf{x})\Big)^\top\cdot\textbf{e},\varepsilon\in\mathbb{R}^N \\ ε=Flatten(EΩ(x))⊤⋅e,ε∈RN
每个LoRA的门控值为
G ( ε i ) = exp ( ε i / τ ) ∑ j = 1 N exp ( ε j / τ ) \mathcal{G}(\varepsilon_i)=\frac{\exp(\varepsilon_i/\tau)}{\sum_{j=1}^N\exp(\varepsilon_j/\tau)} \\ G(εi)=∑j=1Nexp(εj/τ)exp(εi/τ)
温度系数 τ \tau τ是可学习的。最终的输出表示为
E ~ Ω ( x ) = ∑ i = 0 N G i ( ε i ) ⋅ E Δ θ i ( x ) \tilde{\textbf{E}}_{\Omega}(\textbf{x})=\sum_{i=0}^N\mathcal{G}_i(\varepsilon_i)\cdot\textbf{E}_{\Delta\theta_i}(\textbf{x}) \\ E~Ω(x)=i=0∑NGi(εi)⋅EΔθi(x)
其中 E ~ Ω ( x ) ∈ R L × d \tilde{\textbf{E}}_{\Omega}(\textbf{x})\in\mathbb{R}^{L\times d} E~Ω(x)∈RL×d并且 G i ( ⋅ ) \mathcal{G}_i(\cdot) Gi(⋅)表示第i个训练的LoRA。整个block的输出是由预训练权重和门控函数输出相加得到的
O ( x ) = F θ ( x ) + E ~ Ω ( x ) \textbf{O}(\textbf{x})=\textbf{F}_{\theta}(\textbf{x})+\tilde{\textbf{E}}_{\Omega}(\textbf{x}) \\ O(x)=Fθ(x)+E~Ω(x)