哈夫曼树与哈夫曼编码-编程知识

一、哈夫曼树相关概念

路径：从树中的一个节点到另一个节点之间的分支构成两个节点间的路径。

节点的路径长度：两节点间路径的分支数（路径的个数）

树的路径长度（TL）：从根节点到树中每一个点的路径长度之和。

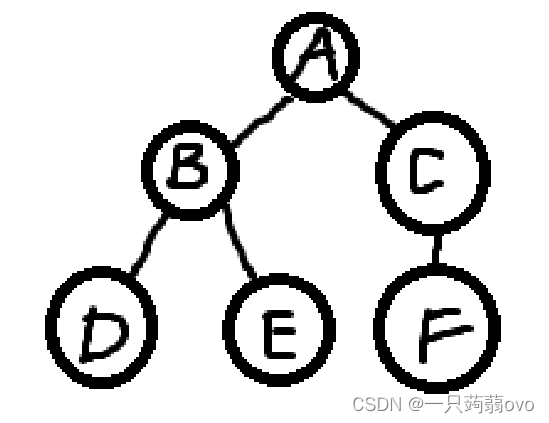
路径长度：

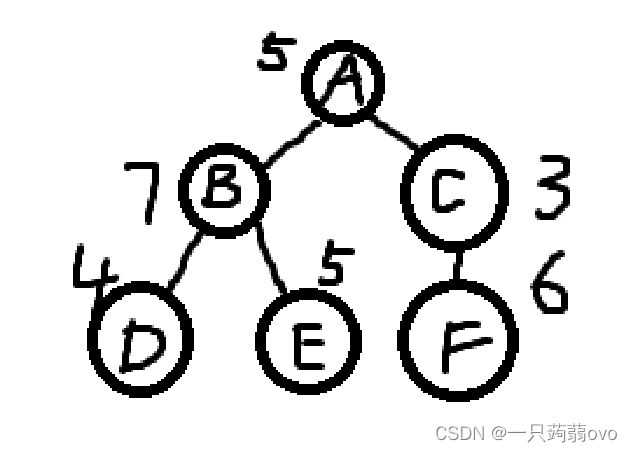
节点A到A，B，C，D，E，F的路径长度分别为0，1，1，2，2，2

树的路径长度（TL）：

节点A到树中每个节点的路径之和　TL=0+1+1+2+2+2=8

权（权重）：将树中的节点赋值（具体实际意义与场合有关）。

节点的带权路径长度：从根节点到该节点之间的路径长度与节点上权的乘积。

树的带权路径长度（WPL）：树中所有叶子节点的带权路径长度之和

WPL＝４＊２＋５＊２＋６＊２＝３０

哈夫曼树：最优二叉树，带权路径长度（WPL）最小的树。

二、哈夫曼树构造方法

１.ｎ个给定权值的节点构成ｎ棵树（１个森林），每个树都有且仅包含一个节点（不重复）

２.选择两棵最小节点权值的树结合构成一棵新的二叉树，并且新二叉树的根节点的权值为其左右子树上根节点的权值之和．

３.在森林中删除这两棵树，并且将新二叉树加入森林

４.重复２－３操作，直至森林中仅剩一棵树为止，为哈夫曼树

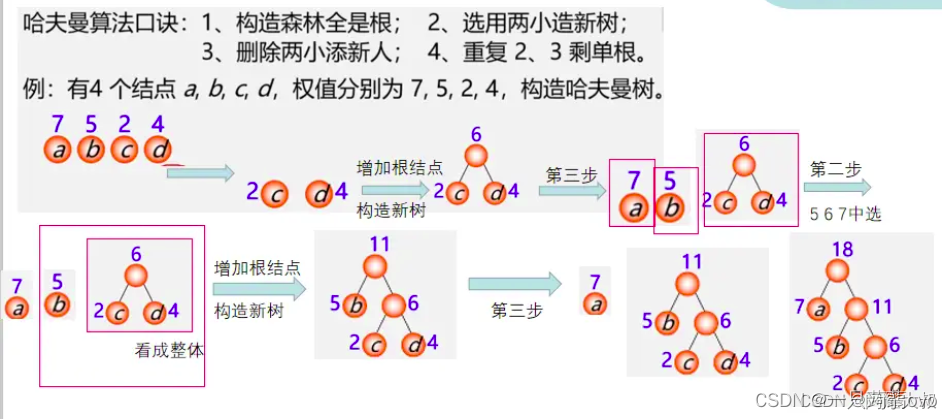
根据哈夫曼树的构建可以得出：

１.初始时有ｎ棵二叉树，经过ｎ－１次合并成为哈夫曼树

２.ｎ－１次合并产生ｎ－１个新节点，新节点都是具有两个孩子的分支节点

哈夫曼树中共有n+n-1 =2n-1个结点，且其所有的分支结点的度均不为1。

三、代码实现哈夫曼树

构建哈夫曼树：需要每次根据各个节点的权重值，筛选出其中最小且无父的两个节点，然后构建二叉树　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　查找权值最小的两个节点：从数组起始位置开始，首先找到两个无父的节点（还未与其他树结合构建），然后和后续无父的节点作比较

１.如果比两个节点中较小的那个还小，则保留这个节点，删除较大的节点

２.如果介于两个权重值之间，替换较大的节点

查找权值最小节点的代码：

//HT数组中存放的哈夫曼树，end表示HT数组中存放结点的最终位置，s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
void Select(HuffmanTree HT, int x, int *s1, int *s2)
{int min1,min2;int i=1;//找到还没构建树的结点while(HT[i].parent!=0 && i<=x){i++;}min1=HT[i].weight;*s1=i;i++;while(HT[i].parent!=0 && i<=nx{i++;}//对找到的两个结点比较大小，min2为较大的，min1较为小的if(HT[i].weight<min1){min2=min1;*s2=*s1;min1=HT[i].weight;*s1=i;}else{min2=HT[i].weight;*s2=i;}for(int j=i+1;j<=nxj++){//如果有父结点，直接跳过，进行下一个if(HT[j].parent!=0){continue;}//如果比最小的还小if(HT[j].weight<min1){min2=min1;min1=HT[j].weight;*s2=*s1;*s1=j;}//如果介于两者之间else if(HT[j].weight>=min1 && HT[j].weight<min2){min2=HT[j].weight;*s2=j;}}
}

构建哈夫曼树代码：

//HT为地址传递的存储哈夫曼树的数组，w为存储结点权重值的数组，n为结点个数
void CreateHuffmanTree(HuffmanTree *HT,int *w,int n)
{int m=2*n-1; // m为哈夫曼树总节点数，n为叶子结点*HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); // 0号位置不用HuffmanTree p=*HT;// 初始化哈夫曼树中的所有结点for(int i=1;i<=n;i++){(p+i)->weight=*(w+i); // p[i].weight=w[i](p+i)->parent=0;(p+i)->left=0;(p+i)->right=0;}//从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点for(int i=n+1;i<=m;i++){(p+i)->weight=0;(p+i)->parent=0;(p+i)->left=0;(p+i)->right=0;}//构建哈夫曼树for(int i=n+1;i<=m;i++){int s1,s2;Select(*HT,i-1,&s1,&s2);(*HT)[s1].parent=(*HT)[s2].parent=i;  //新添第i个节点(*HT)[i].left=s1;(*HT)[i].right=s2;(*HT)[i].weight=(*HT)[s1].weight+(*HT)[s2].weight;}
}

四、哈夫曼编码（贪心思想）

哈夫曼编码也翻译为赫夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，属于一种程序算法，赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%～90%之间赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，称之为最佳编码

在远程通讯中，将待传字符转化成二进制的字符串。

１.在通信领域中信息的其他处理方式

①定长编码：字符通过ASCII代码转化，再用二进制表示

将 i like like like java do you like a java 定长编码 // 共40个字符(包括空格)

105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97 //对应Ascii码

01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 01110110 01100001 //对应的二进制按照二进制来传递信息，总的长度是 359 (包括空格)

定长编码的方法保证了信息传递的正确性，但是从上述过程可以看出，效率并不是最优的

②变长编码：将各个字符按照出现的次数进行编码，即出现次数越多的，编码越小．（出现次数越多的尽可能使其编码越小）

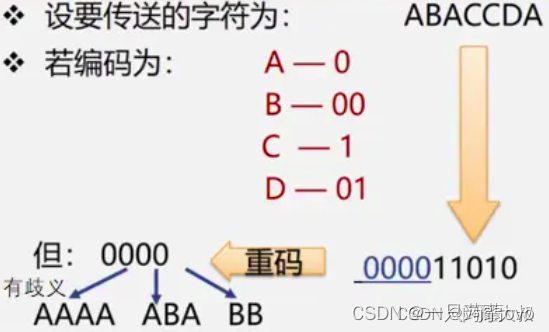
通过上述图例，可以很明显看出存在编码多义，即一段编码可以得出多种结果，显然是错误的方法．

若需要运用上述思想，可以作前缀编码（每个字符的编码都不能是其他字符编码的前缀），例如上述　A=0 与 B=00，A的编码就是B编码的前缀．而哈夫曼编码就是运用这一想法．

２.哈夫曼编码

①统计每个字符在字符串中出现的次数（出现次数越多，要求编码越短）

②利用哈夫曼树的特点，以每个字符出现的次数作为权值，权越大的叶子节点离根越近，构造哈夫曼树

③在哈夫曼树的左分支标上０，右分支标上１

则某个节点的编码即为从根节点到该节点路径上的标号连接而成，这样保证了前缀编码，不出现歧义

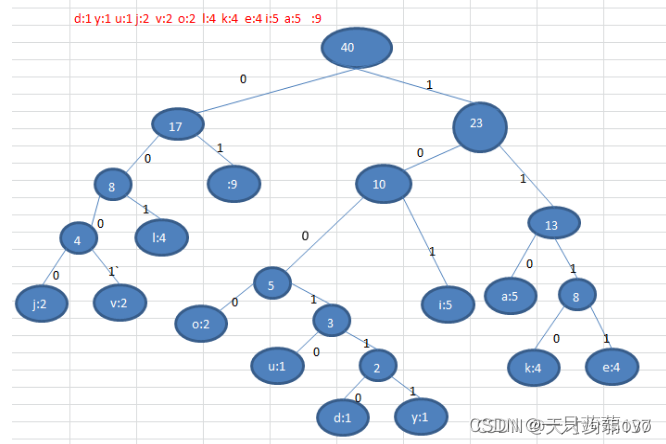
３.哈夫曼编码代码实现

首先根据数据构建哈夫曼树（上述代码已讲），再通过遍历哈夫曼树找出字符对应的二进制编码．

法一：从叶子节点一直找到根节点，逆向记录途中的标记．

法二：从根节点出发，一直到叶子节点，记录途中经过的标记

//HT为哈夫曼树，HC为存储结点哈夫曼编码的二维动态数组，n为结点的个数
void HuffmanCoding(HuffmanTree HT, HuffmanCode *HC,int n)
{*HC=(HuffmanCode) malloc((n+1)*sizeof(char*));char *cd=(char *)malloc(n*sizeof(char)); //存放结点哈夫曼编码的字符串数组cd[n-1]='\0';//字符串结束符for(int i=1;i<=n;i++){//从叶子结点出发，得到的哈夫曼编码是逆序的，需要在字符串数组中逆序存放int start=n-1;//当前结点在数组中的位置int c=i;//当前结点的父结点在数组中的位置int j=HT[i].parent;// 一直寻找到根结点while(j!=0){// 如果该结点是父结点的左孩子则对应路径编码为0，否则为右孩子编码为1if(HT[j].left==c)cd[--start]='0';elsecd[--start]='1';//以父结点为孩子结点，继续朝树根的方向遍历c=j;j=HT[j].parent;}//跳出循环后，cd数组中从下标 start 开始，存放的就是该结点的哈夫曼编码(*HC)[i]=(char *)malloc((n-start)*sizeof(char));strcpy((*HC)[i],&cd[start]);}//使用malloc申请的cd动态数组需要手动释放free(cd);
}

学习博文

【数据结构与算法】-哈夫曼树(Huffman Tree)与哈夫曼编码_哈夫曼编码树-CSDN博客

哈夫曼编码详解-CSDN博客