1,概念
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈 顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈(push):栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈(pop
public static void main(String[] args) {
Stack<Integer> s = new Stack();
s.push(1);
s.push(2);
s.push(3);
s.push(4);
System.out.println(s.size()); // 获取栈中有效元素个数---> 4
System.out.println(s.peek()); // 获取栈顶元素---> 4
s.pop(); // 4出栈,栈中剩余1 2 3,栈顶元素为3
System.out.println(s.pop()); // 3出栈,栈中剩余1 2 栈顶元素为3
if(s.empty()){
System.out.println("栈空");
}else{
System.out.println(s.size());
}
}
):栈的删除操作叫做出栈。出数据在栈顶。
栈在现实生活中的例子:

2 栈的使用
public static void main(String[] args) {
Stack<Integer> s = new Stack();
s.push(1);
s.push(2);
s.push(3);
s.push(4);
System.out.println(s.size()); // 获取栈中有效元素个数---> 4
System.out.println(s.peek()); // 获取栈顶元素---> 4
s.pop(); // 4出栈,栈中剩余1 2 3,栈顶元素为3
System.out.println(s.pop()); // 3出栈,栈中剩余1 2 栈顶元素为3
if(s.empty()){
System.out.println("栈空");
}else{
System.out.println(s.size());
}
}
如图:
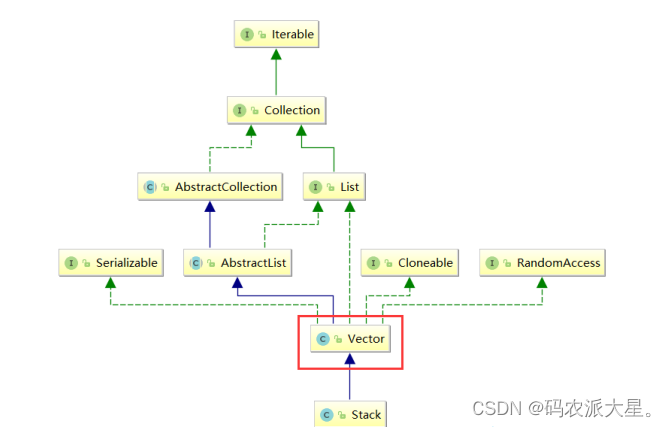
从上图中可以看到,Stack继承了Vector,Vector和ArrayList类似,都是动态的顺序表,不同的是Vector是线程安 全的。
3 模拟实现一个栈
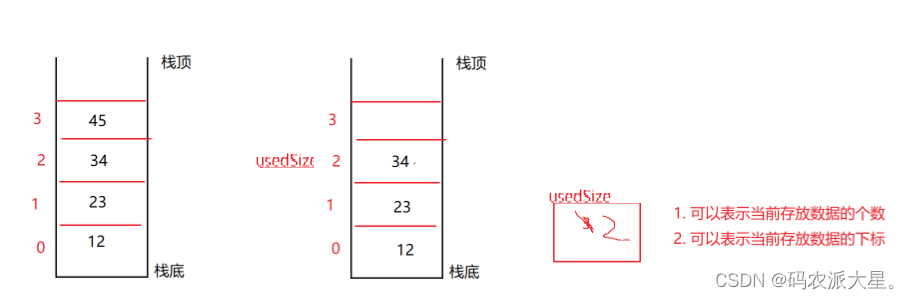
import java.util.Arrays;public class MyStack {public int[] elem;public int usedSize;public MyStack(){this.elem = new int[10];}public void push(int val){if(isFull()){//扩容elem = Arrays.copyOf(elem,2*elem.length);}elem[usedSize] = val;usedSize++;}public boolean isFull(){return usedSize == elem.length;}public int pop(){if(empty()){return -1;}int oldval = elem[usedSize-1];usedSize--;return oldval;}public int peek(){if(empty()){return -1;}int oldval = elem[usedSize-1];return oldval;}public boolean empty(){return usedSize == 0;}}
public class Test {public static void main(String[] args) {MyStack myStack = new MyStack();myStack.push(1);myStack.push(2);myStack.push(3);System.out.println(myStack.pop());System.out.println(myStack.peek());}
}
4 栈的应用场景
1. 改变元素的序列
1. 若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是(c)
: 1,4,3,2
B: 2,3,4,1
C: 3,1,4,2
D: 3,4,2,1
解析:1、2、3入栈以后,3再出栈,此时栈顶为2,只能出2,不能出其他
2.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺 是( B)
A: 12345ABCDE
B: EDCBA54321
C: ABCDE12345
D: 54321EDCBA
2 逆波兰表达式求值 OJ链接
我们先来了解一下中缀表达式和后缀表达式:
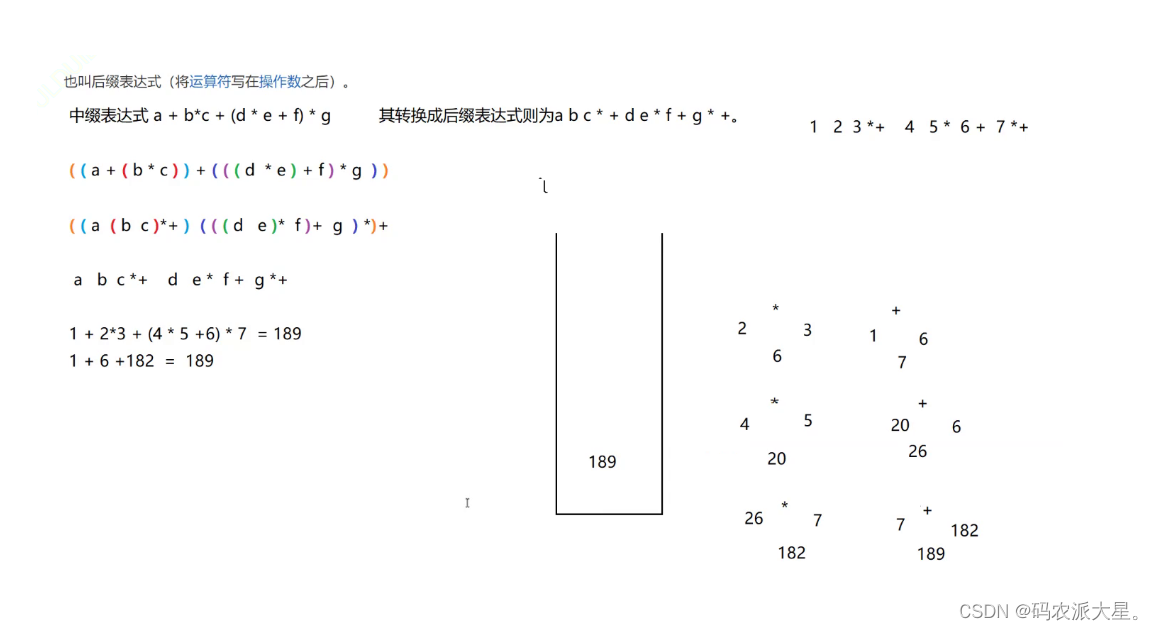
class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for(int i = 0; i< tokens.length;i++){String tmp = tokens[i];if(!isOpearation(tmp)){Integer val = Integer.valueOf(tmp);stack.push(val);}else{// + - / *Integer val2 = stack.pop();Integer val1 = stack.pop();switch(tmp){case "+":Integer ret1 = val1+val2;stack.push(ret1);break;case "-":Integer ret2 = val1-val2;stack.push(ret2);break;case "*":Integer ret3 = val1*val2;stack.push(ret3);break;case "/":Integer ret4 = val1/val2;stack.push(ret4);break; } } }return stack.pop();}public boolean isOpearation(String s){if(s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")){return true;}return false;}
}3. 括号匹配 OJ链接
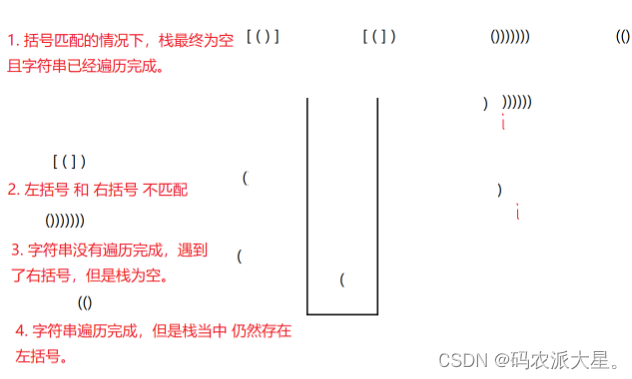
class Solution {public boolean isValid(String s) {Stack<Character> stack = new Stack<>();for(int i = 0; i< s.length(); i++){char ch = s.charAt(i);//1,左括号入栈if(ch == '(' || ch == '{' || ch == '['){stack.push(ch);}else{//2.遇到了右括号if(stack.empty()){return false;}else{//3.取栈顶元素的左括号看和当前右括号是否匹配char chL = stack.peek();if(chL == '(' && ch == ')' || chL == '[' && ch == ']'||chL == '{' && ch == '}'){//4.证明当前一对括号是匹配的stack.pop();}else{//5,当前括号不匹配return false;}}}}return stack.empty();}
}4 出栈入栈次序匹配OJ链接
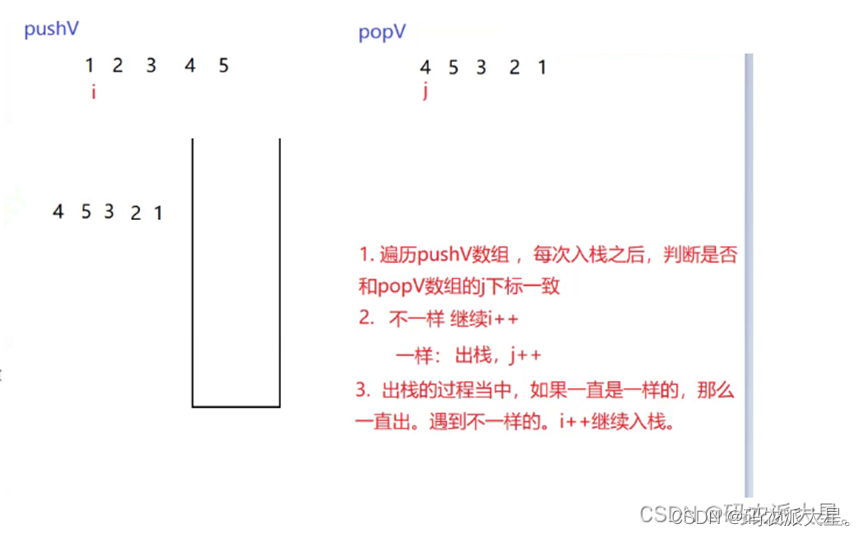
public boolean IsPopOrder (int[] pushV, int[] popV) {// write code hereStack<Integer> stack = new Stack<>();int j = 0;for(int i = 0; i<pushV.length;i++){stack.push(pushV[i]);while(j<popV.length && !stack.empty()&& stack.peek() == popV[j]){stack.pop();j++;}}return stack.empty();}
}