一、贪心算法
贪心算法是指:在对问题求解时,总是做出在当前看来是最好的选择,而不从整体最优考虑,做出的仅是在某种意义上的局部最优解。 贪心算法不是对所有问题都能得到整体最优解,但能产生整体最优解或者其近似解。
基本思路:
通过一种贪心的想法,使得得到当前的局部最优解,从而拓展至整体最优解(不一定)。所求问题的整体最优解可以通过一系列局部最优的选择,换句话说,当考虑做何种选择的时候,我们只考虑对当前问题最佳的选择而不考虑子问题的结果。这是贪心算法可行的第一个基本要素。贪心算法以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解。
贪心算法的弊端:
1.不能保证得到的最后解一定是最佳的,可能存在近似解(不保证一定的正确)。
2.不能用来求最大或最小解问题。
3.只能求满足某些约束条件的可行解的范围。
二、活动选择问题
1.题目描述:
假定有一个n个活动(activity)的集合S={a1, a2, ..., an},这些活动使用同一个资源(例如一个阶梯教室),而这个资源在某个时刻只能供一个活动使用。 每个活动ai都有一个开始时间si和一个结束时间fi。 如果两个活动[si, fi)和[sj, fj)不重叠,则称它们是兼容的
目标: 找到互相兼容的最大活动子集

互相兼容的最大活动子集样例:
2.贪心思想的策略
针对每个新活动,计算其与已经举办过的活动之间的兼容性。
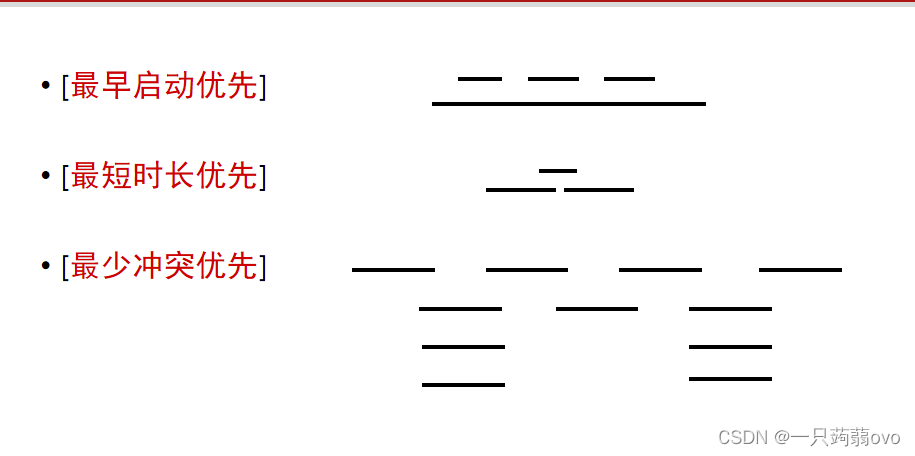
①最早启动优先:对于所有活动,以 si 升序排列
②最短时长优先:以 fi - si 升序排列
③最少冲突优先:对于每个 i,统计与其冲突的活动数量 ci ,以 ci 升序排列
④最早结束优先:以 fi 升序排列
贪心算法不保证正确性,以上四种想法,对于 ① ② ③ 均存在反例验证出其错误。
3.贪心思想的正确性验证(最早结束优先):
设E={a1,a2,.....,an}为活动集合,且E中的活动是按照活动结束时间升序排列的,显然a1为最早结束。设A是问题的一个最优解,明显A是E的一个子集,设A的第一个活动为k
① 若 k = a1,则A的第一个活动就是最早结束的,故A是以贪心选择开始的最优解
② 若 k ≠ a1,设集合B=(A-{k})∪a1 ,即用活动a1可替换掉活动k
因为的结束时间小于
,故
比
提前结束。另外由于A中的活动是相容的,故B中的活动也相容。 又因为A中的活动个数和B中的活动个数相同,故B也是最优解(需要注意的是最优解一般不唯一)。所以 B 是一个以贪心选择活动 a1 为开始后的最优解。
或者另一种想法:
对于最早结束的第一个活动 a1, 局部最优解考虑a1,再考虑 a2 :
若 s2>f1 a1,a2 兼容,则问题只需要考虑 a2 ~ an,问题变成了子问题 a2 ~ an 。
若 s2<f1 a1,a2 冲突,不考虑 a1, 令 a2 为最优解的第一个活动,则此时在 a3~an 的最优解中,加上 a1 或者 a2 的活动(不冲突时),才成为整体的最优解。此时考虑 a1 或者 a2 都是最优解,活动兼容的个数都相同,所以此贪心思想是正确的。
4. 此外该问题还存在另一种贪心思想:
选择最晚开始的活动依次排序考虑,其他与上述思想一致。
三、拓展问题:最少资源投入
1.问题描述
假定有一个n个活动的集合S={a1, a2, ..., an},这些活动可以同时使用多个资源(例如一个阶梯教室),但一个资源在某个时刻只能供一个活动使用。 每个活动 ai 都有一个开始时间 si 和一个结束时间 fi 。 如果两个活动 [ si , fi ) 和 [ sj , fj ) 不重叠,则称它们是兼容的
目标: 找到最少资源数量,使得所有活动能够正常举行.
2.贪心思想:
①首先将所有课程按照开始时间升序排列,并且将每门课程赋予任何可兼容的教室。
②通过维护一个优先队列,按照结束时间升序排列(队列首端的结束时间最早),队列中的每个元素对应着各教室的结束时间。
③这样当新的一个活动加入时,只需要与队首元素对应的结束时间比较,若大于结束时间则直接替换,若小于最早的结束时间,则需要加入一个元素(添加一个新的教室)。
四、分数背包问题
1.问题描述
给定背包容量和一些物品,每个物品有重量和价值两个属性。允许只取一个物品的一部分加入背包,求问如何才能使背包装的物品价值最大。
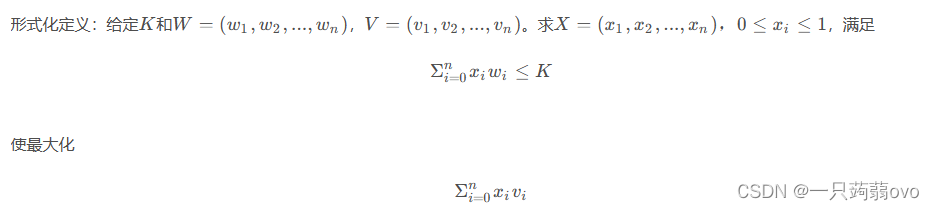
背包问题实质上是一个线性规划问题,可以用单纯形法、椭球法、内点法(后两者均为多项式时间算法)等求解。但在这个问题中,简单的贪心算法就能够求出最优解。
2.贪心思想:
既然能够取某个物品的一部分加入背包,则可以先计算出每个物品的单位重量对应的价值,再从高到低依次排序,依次放入背包,直至达到背包的总容量(贪心)。
即先取最划算的,从最划算的依次往下取。


![[MySQL数据库] Java的JDBC编程(MySQL数据库基础操作完结)](https://img-blog.csdnimg.cn/direct/aa3ecdeb921e41a3907299ea61649b56.png)