给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数
是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
- 例如,
121是回文,而123不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
提示:
- -231 <= x <= 231 - 1
进阶:你能不将整数转为字符串来解决这个问题吗?
我的解题思路1:
将整数转为字符串->将字符串反转->判断反转后的字符串是否与之前字符串相同,如果相同则是回文数,否则不是回文数。
思路1代码:
class Solution {public boolean isPalindrome(int x) {String original = x+"";StringBuilder sb = new StringBuilder(original).reverse();String s = sb.toString();if (original.equals(s))return true;return false;}
}
思路2:
将整数转为字符串->分别定义一个下标指向字符串头和尾,以此对比头和尾所指字符是否相同,如果不同则返回false,直到头下标超过尾下标,表示是回文数,返回true
思路2代码
class Solution {public boolean isPalindrome(int x) {String s = x + "";int left = 0, right = s.length()-1;// left指向开始字符,right指向结尾字符while(left<right){if(s.charAt(left)!=s.charAt(right))return false;// 头和尾不相同,返回falseleft++;right--;}// 一直没有不相同的,返回truereturn true;}
}
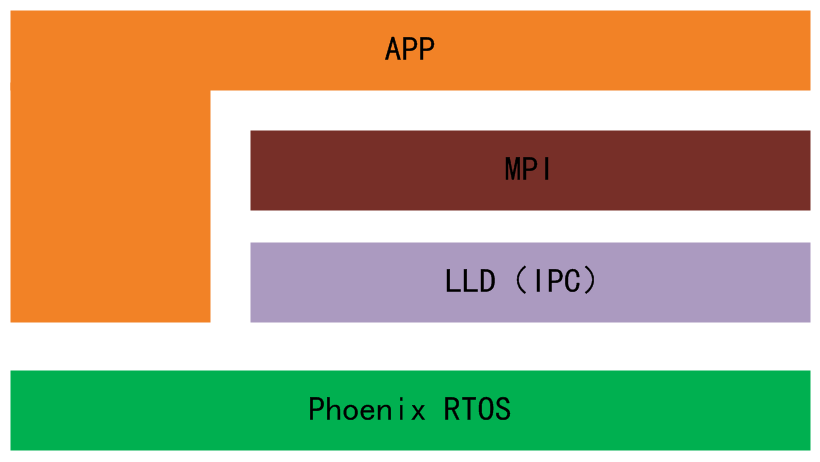
结果:
思路三:直接利用整数运算进行操作
如果小于0,肯定不是回文数
对整数进行尾部取余然后算出反转后的数,比较是否相等,如果相等则是回文数,否则不是
代码
class Solution {public boolean isPalindrome(int x) {// 负数直接返回falseif(x<0)return false;// 使用long类型,防止反转后的数值溢出int型数据long reverse = 0;int original = x;while(x!=0){reverse = reverse*10 + x%10;x = x/10;}if(reverse==original)return true;return false;}
}
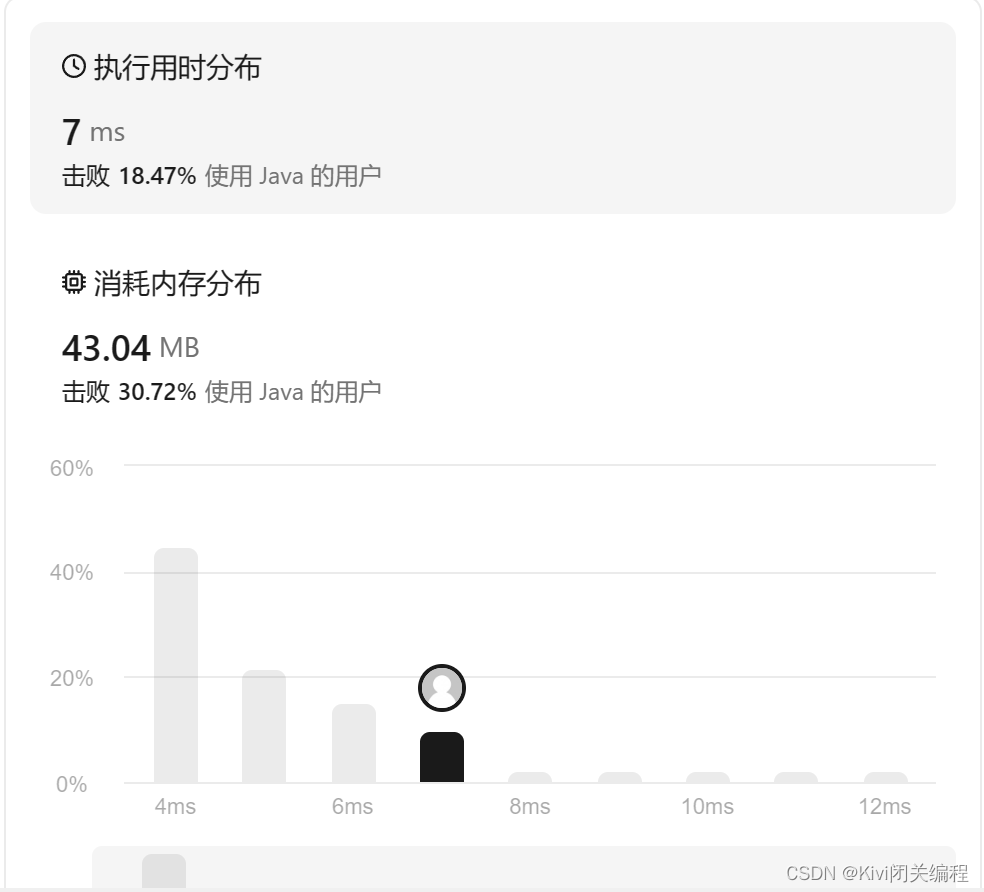
结果:
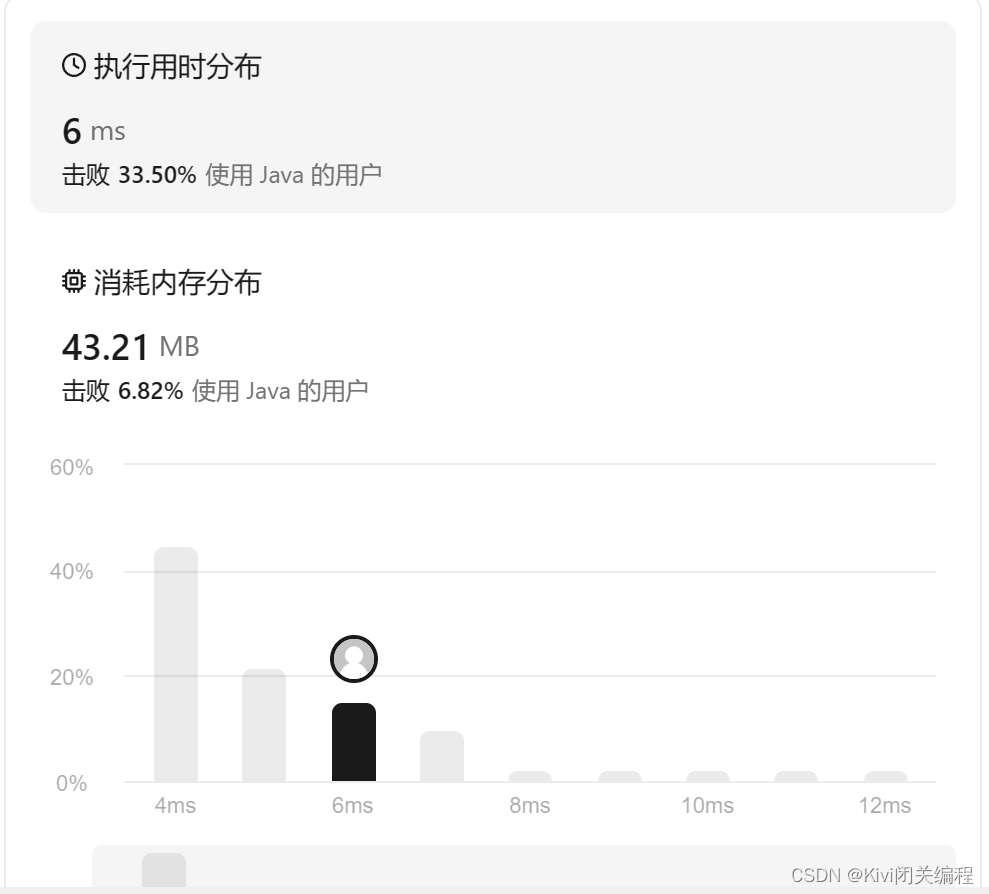
和上述同样的逻辑。只是在防止反转后数值溢出处理使用了判断逻辑,判断int型溢出逻辑可以查看我的第8题讲解文章,即在计算之前判断是否大于int的最大值/10,以及再计算之后的值是否小于0。
修改后代码如下,节省了4个字节的内存:
class Solution {public boolean isPalindrome(int x) {// 负数直接返回falseif(x<0)return false;// 使用long类型,防止反转后的数值溢出int型数据int reverse = 0;int original = x;while(x!=0){if(reverse > Integer.MAX_VALUE/10)return false;reverse = reverse*10 + x%10;if(reverse < 0)return false;x = x/10;}if(reverse==original)return true;return false;}
}
总结:
字符串反转问题:可以将String类型变量转成StringBuilder然后调用reverse()进行反转,最后使用toString()方法转回String类型。
字符串如何转成字符数组:s.toCharArray()函数。
从上述结果也可以看出,字符串处理是速度较慢的,计算机对于数值计算较快。