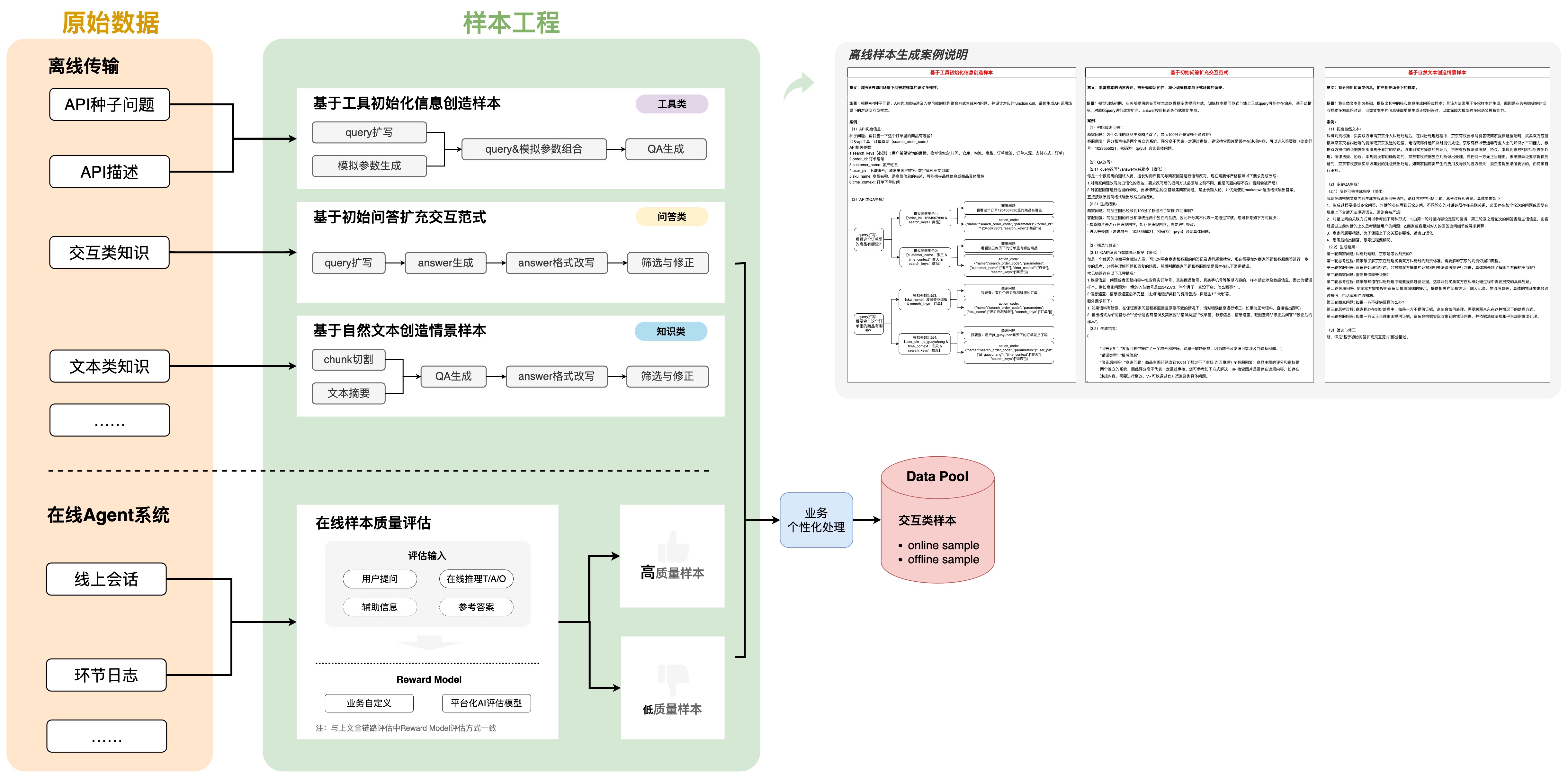
Statement
有一栋 \(n\) 层的楼,居民们要共同发射至少 \(c\) 架纸飞机,楼层高的居民看不到楼层低的居民发射的纸飞机,每位居民会在自己看到的纸飞机数量至少 \(c\) 后停止,实际上它们总共发射了 \(m\) 个纸飞机,现在你有一个 \(a\) 数组记录了每层楼居民发射的飞机数量,部分 \(a_i\) 缺失了即 \(a_i = 0\),你需要找出填补这些 \(a_i\) 的总方案数,答案对 \(10^9 + 7\) 取模。
在当前问题版本中,所有 \(a_i\) 均为 \(0\)。
Solution
记 \(dp_{i,j}\) 表示第 \(i\) 层楼发射飞机 \(j\) 架,枚举发射的飞机数量,转移方程有:
\[dp_{i,j} \leftarrow dp_{i,j} + \sum\limits_{k=0}^{\min(j,c)}dp_{i-1,j-k}
\]
当然你会发现方程缺了什么,注意到我们是从 \(c\) 次发射中选择 \(k\) 次,所以还需要一个系数 \(\binom{c}{k}\),得到最终的柿子:
\[dp_{i,j} \leftarrow dp_{i,j} + \sum\limits_{k=0}^{\min(j,c)}{dp_{i-1,j-k} \times \binom{c}{k}}
\]
最后答案即为 \(dp_{n,m}\)。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9 + 7;
int T, n, C, m, A[10005], dp[105][10005], fac[1000005], invfac[1000005];inline int qpow (int x, int k) {int ret = 1;while (k) {if (k & 1) ret = ret * x % MOD;x = x * x % MOD;k >>= 1;}return ret;
}inline void prefac() {fac[0] = invfac[0] = 1;for (int i = 1; i <= 1000000; i ++)fac[i] = fac[i - 1] * i % MOD;invfac[1000000] = qpow (fac[1000000], MOD - 2);for (int i = 999999; i; i --)invfac[i] = invfac[i + 1] * (i + 1) % MOD;
}inline int Com (int n, int m) {if (m < 0 || m > n) return 0;return fac[n] * invfac[m] % MOD * invfac[n - m] % MOD;
}inline void Dp() {cin >> n >> C >> m;for (int i = 1; i <= m; i ++)cin >> A[i];dp[1][C] = 1;for (int i = 2; i <= n; i ++) {for (int j = C; j <= m; j ++) {for (int k = 0; k <= min (j, C); k ++) {dp[i][j] = (dp[i][j] + Com (C, k) * dp[i - 1][j - k] % MOD) % MOD;}}}cout << dp[n][m] << '\n';for (int i = 1; i <= n; i ++) {for (int j = C; j <= m; j ++) {for (int k = 0; k <= min (j, C); k ++) dp[i][j] = 0;}}
}signed main() {cin.tie (0) -> sync_with_stdio (0);cout.tie (0) -> sync_with_stdio (0); cin >> T, prefac();while (T --) Dp();return 0;
}